浙江省杭嘉湖金四县区2020-2021学年高二下学期6月份调研考试数学试题含答案

这是一份浙江省杭嘉湖金四县区2020-2021学年高二下学期6月份调研考试数学试题含答案，共13页。
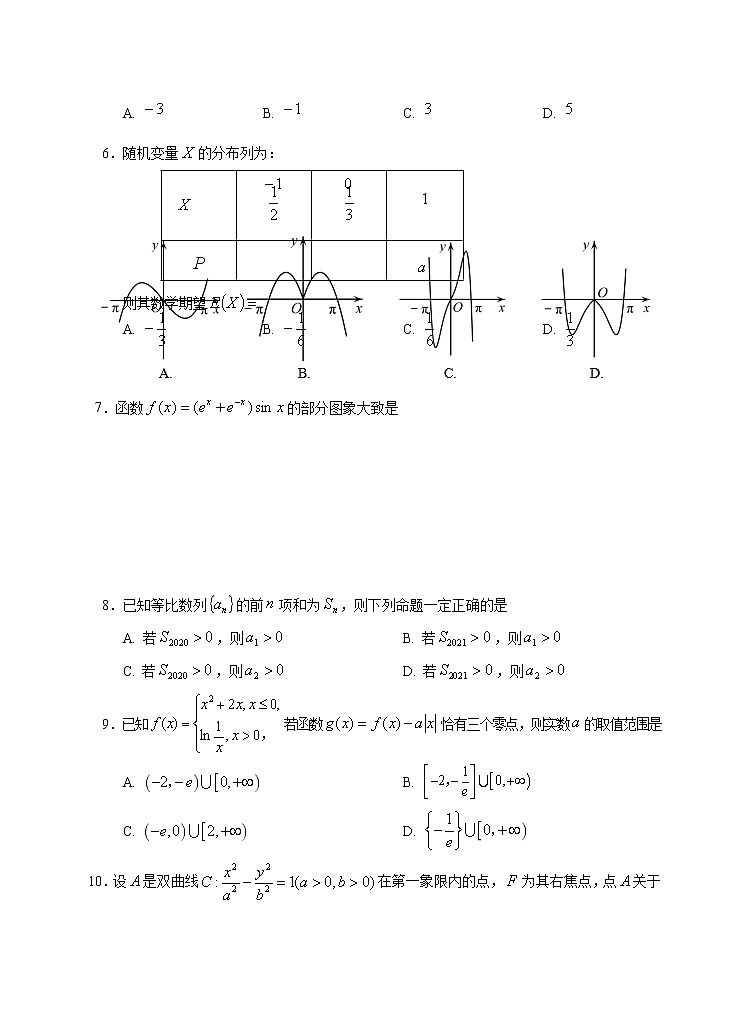
2021年6月杭嘉湖金四县区教研联盟高二调研测试数学试题卷本科试题卷分选择题和非选择题两部分，全卷共4页，满分150分，考试用时120分钟.考生注意：1. 答题前，请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上.2. 答题时，请按照答题纸上“注意事项”的要求，在答题纸相应的位置上规范作答，在本试题卷上的作答一律无效.选择题部分（共40分）一、选择题（本大题共10小题，每小题4分，共40分. 在每小题给出的四个选项中，只有一项是符合要求的）  1．已知集合，，则   A.     B.     C.     D.  2．已知R，若i(i为虚数单位是实数，则   A.             B.              C.               D.  3．若为两条不同的直线，为平面，且，则“”是“”的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件       D. 既不充分也不必要条件 4．在中国古建筑中，为了保持木构件之间接榫（“榫”，即    指木质构件利用凹凸方式相连接的部分）的地方不活动，    需要将楔子捶打到榫子缝里.如图是一个楔子的三视图   （单位：cm），则这个楔子的体积（单位：cm3）是 A. 4              B. 6 C. 8               D. 12 5．若实数满足约束条件则的最大值为 A.             B.           C.             D.  6．随机变量的分布列为：                                           P    则其数学期望     A.            B.           C.          D. 7．函数的部分图象大致是      8．已知等比数列的前项和为，则下列命题一定正确的是 A. 若，则     B. 若，则 C. 若，则     D. 若，则 9．已知若函数恰有三个零点，则实数的取值范围是  A.      B.  C.       D. 10．设是双曲线在第一象限内的点，为其右焦点，点关于原点的对称点为，且，，则双曲线的离心率的取值范围是A.      B.        C.        D. 非选择题部分（共110分）二、填空题（本大题共7小题，多空题每题6分，单空题每题4分，共36分） 11．已知则   ▲   ；若，则   ▲   .12．的展开式中，各项系数的和为   ▲   ，常数项为   ▲   .（用数字作答）13．已知直线和圆相交于两点，则该圆的圆心坐标为   ▲   ，弦长   ▲   .14．在锐角中，角的对边分别为，且. 则角的大小为   ▲   ，当时，的最小值是   ▲   .15．如图，在正方体，与相交于点，则平面与平面所成角为   ▲   度. 16．已知，且，若不等式    恒成立，则实数的取值范围是   ▲   . 17．如图，在直角中，.    分别是边上的点，，，    若是直线上的动点，则的最小值为   ▲   .三、解答题（本大题共5小题，共74分.解答题应写出文字说明、证明过程或演算步骤）18．(本题满分14分)    已知函数.    (Ⅰ) 求函数的最小正周期和单调增区间；(Ⅱ) 求函数在上的值域.19．(本题满分15分)    如图，在四棱锥中，平面平面，底面四边形为直角梯形，，,，，为线段的中点，过的平面与线段分别交于点.(Ⅰ) 求证：∥；(Ⅱ) 若为棱上靠近点的三等分点，求直线与平面所成角的正弦值.     20．(本题满分15分)    已知数列为等差数列，且，，数列满足，其中为数列的前项和，N*.(Ⅰ) 求数列，的通项公式；(Ⅱ) 若满足：，求的前项和.  21．(本题满分15分)        如图，已知椭圆的右顶点为，且是抛物线的焦点，直线是抛物线的准线.    (Ⅰ) 求抛物线的方程；    (Ⅱ) 设上两点关于轴对称，直线与        椭圆交于点，直线与轴相交于        点，求面积的最大值.   22．(本题满分15分)    已知，R.   (Ⅰ) 当时，求函数的单调区间；    (Ⅱ) 证明：当，恒成立. 
2021年6月杭嘉湖金四县区教研联盟高二调研测试数学参考答案一、选择题（本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合要求的） 题号12345678910答案BDABCACBDC二、填空题（本大题共7小题，多空题每题6分，单空题每题4分，共36分） 11.        ；       .        12.       ；       .      13.       ；       . 14.             ；       .   15.        .   16.          .    17.        .三、解答题（本大题共5小题，共74分.解答题应写出文字说明、证明过程或演算步骤） 18. (本题满分14分)    (Ⅰ)..........................................................................1分         ..................................................................2分        的最小正周期................................................................................4分        令，得，...................7分        的单调增区间为....................................................8分   （Ⅱ)由（Ⅰ）知，，，...................................................................10分，..........................................................................................12分.  的值域为.............................................................................................14分(本题满分15分）(Ⅰ)已知底面四边形为直角梯形，，又为中点，，四边形为平行四边形，.............................2分平面,平面,平面.....................................4分 又平面,平面平面......................7分  (Ⅱ)解法一：作，垂足为，连.，.由已知平面平面，平面平面，平面.........................................................................................................9分  又平面，平面平面,又平面平面平面.是直线与平面所成的角.........12分      在中，，，中，，.    在中， ,得，    可得. 在中,.    直线与平面所成角的正弦值为........................................................15分        (Ⅱ)解法二：由已知为中点，,又平面平面，平面平面，平面,，又由已知可得，两两垂直.现以为原点，所在直线为轴，所在直线为轴，所在直线为轴，建立空间直角坐标系.由已知可得：..........................................................9分 则，，设平面的一个法向量为，则有,取，则.平面的一个法向量为，可求得..............12分 设直线与平面所成角为，则.   直线与平面所成角的正弦值为.........................................................15分  20. (本题满分15分)(Ⅰ)设的公差为,则,......................................................................1分，...............................4分     由已知时，得，.....................................................6分设可得，即. .......................8分(Ⅱ)由已知，.............................................................................9分   令①   则②...................11分       ①－②得       .............................................................13分得...............................................................................15分21. (本题满分15分)    (Ⅰ)由已知椭圆右顶点为...........................................................................................2分抛物线的焦点为,，，...........................................................4分        抛物线的方程为......................................................................................5分   (Ⅱ)设直线的方程为，令，得.       联立得.       点坐标为..............................................................................7分方程为.令得,的坐标为，...................................................................................12分...................................................13分,当且仅当即取等号.面积的最大值为            ..........................................................................15分22. (本题满分15分)   (Ⅰ)由已知,................................................................................................................1分当时，,,............................2分       令,,.........4分       的增区间为，减区间为............................................6分    (Ⅱ)，，        只需证明恒成立........................................................................8分        下面证明.       证法一：  令，,.........................................................10分令，则，可得       在上递减，又,  ，可得.        当时，，当时，,       在上递增，在上递减，在上的最大值为,..............................................13分 在上递减,. 又                                      ， 恒成立.恒成立. 恒成立...............................................................................................15分   证法二：        令，，令，令,在单调递增，在单调递减.，，即...............................11分可得，..........................................................................................13分从上可得，恒成立恒成立...............................................................................................15分