初中数学第十七章 勾股定理综合与测试图文ppt课件

这是一份初中数学第十七章 勾股定理综合与测试图文ppt课件，共37页。PPT课件主要包含了学习目标，回顾旧知，导入新知，合作探究，巩固新知，解在△ABC中，找找最大数，勾股定理逆定理的应用，实际应用，勾股数等内容，欢迎下载使用。

1.熟练运用勾股定理及其逆定理解决实际问题。2.学会将实际问题构建成数学模型，并运用勾股定理的逆定理解决。
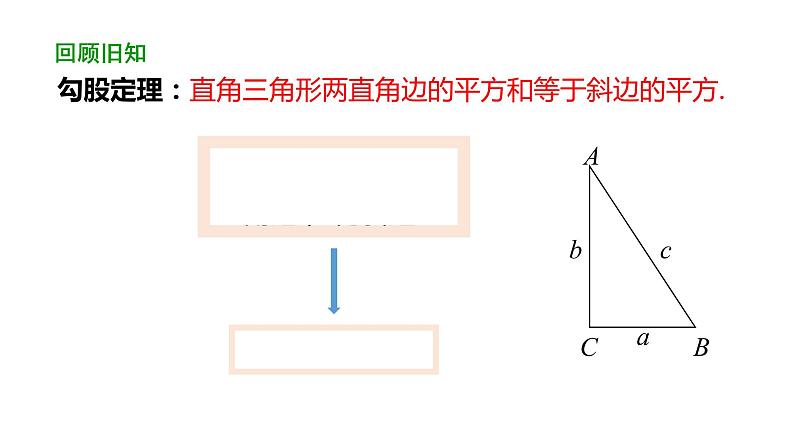
勾股定理：直角三角形两直角边的平方和等于斜边的平方.
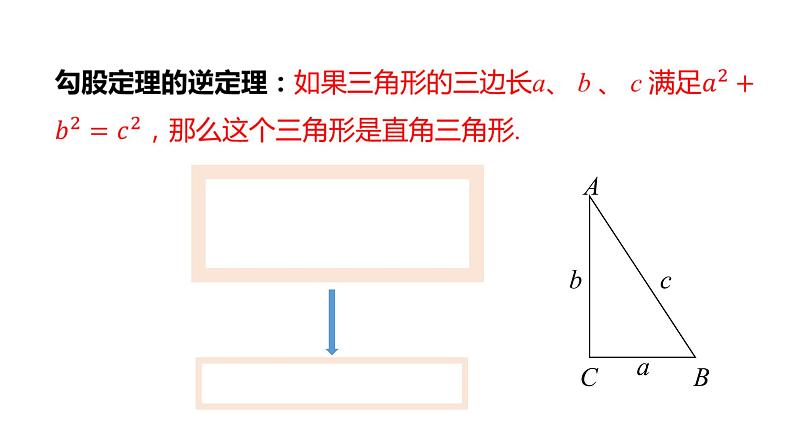
互逆命题：如果两个命题的题设、结论正好相反，那么这两个命题叫做互逆命题.如果把其中一个叫做原命题，那么另外一个叫做它的逆命题.
互逆定理：一般地，如果一个定理的逆命题经过证明是正确的，那么它也是一个定理，称这两个定理互为逆定理，其中一个定理叫做另外一个定理的逆定理.
思考 我们已经学会用勾股定理解决实际问题，那么勾股定理的逆定理在实际生活中有哪些应用呢？
船只在航行的时候需要确定方向和位置.
例2 如图，某港口 P 位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行， “远航”号每小时航行 16n mile， “海天”号每小时航行 12n mile.它们离开港口一个半小时后分别位于点 Q、R 处，且相距 30n mile.如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？
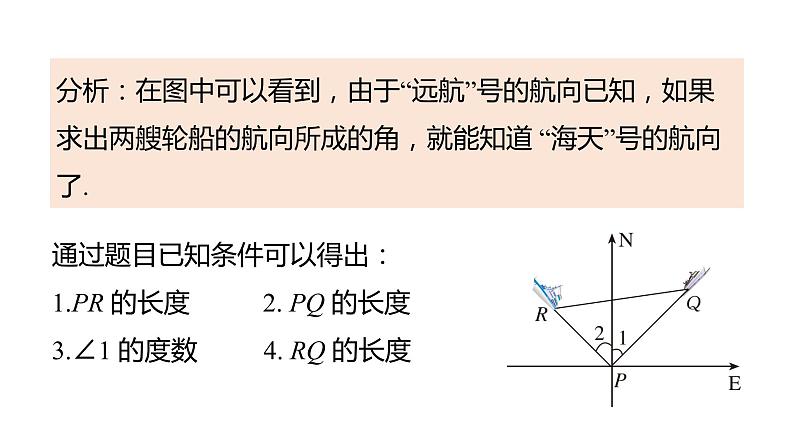
分析：在图中可以看到，由于“远航”号的航向已知，如果求出两艘轮船的航向所成的角，就能知道 “海天”号的航向了.
通过题目已知条件可以得出：1.PR 的长度 2. PQ 的长度3.∠1 的度数 4. RQ 的长度
解：根据题意， PQ=16╳1.5=24， PR=12╳1.5=18， RQ=30.
所以∠RPQ=90〫.
由“远航”号沿东北方向航行可知， ∠1=45〫 .因此∠2=45〫 ，即“海天”号沿西北方向航行.
1. A、B、C 三地的两两距离如图所示，A 地在 B 地的正东方向，C 地在 B 地的什么方向？
解析：根据图示的距离，可以判断出以 A、B、C 三地位置构成的三角形是直角三角形.
所以△ABC是直角三角形，且∠B=90〫，所以 C 地在 B 地的正北方向 .
2.如图，在四边形ABCD中，AB=3，BC=4，CD=12，AD=13， ∠B=90〫.求四边形ABCD的面积.
解析：△ABC是直角三角形，所以可以求出斜边 AC. 根据 AC、CD、AD 的长度及勾股定理的逆定理可以判定△ACD也是直角三角形.
判断一组数是否为勾股数的步骤
看：看是不是三个正整数；
算：计算最大数的平方与两个较小的数的平方和；
判：若两者相等，则这三个数是一组勾股数，否则，不是一组勾股数.
（3）一组勾股数中的各数都乘以相同的正整数可以得到一组新的勾股数，即如果a，b，c是一组勾股数，那么ak，bk，ck（k为正整数）也是一组勾股数.
1.判断下列各组数是不是勾股数.（1）8、12、16；（2）12、16、20；（3）0.9、1.2、1.5
2.给出下列数组：①5、12、13；②2、3、4；③2.5、6、6.5；④21、20、29.其中勾股数的组数是（ ）.A.4 B.3 C.2 D.1
3.如图，张三决定挖一块长方形的菜地， 在挖完后测量了一下发现AB=CD=4m，AD=BC=3m，AC=4.5m，请你帮忙计算一下其挖的菜地是否为长方形.
实际问题构建成数学模型，利用逆定理去求解.
能够成为直角三角形三条边长的三个正整数.
1．如图，有一块直角三角形纸片，∠C＝90°，AC＝4 cm，BC＝3 cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为( )A．1 cm B．1.5 cmC．2 cm D．3 cm
4．如图，在长方形纸片ABCD中，已知AD＝8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF＝3，则AB的长为( )A．3 B．4 C．5 D．6
5．如图，将长方形ABCD沿对角线BD折叠，使点C和点C′重合，BC′交AD于点E，若AB＝4，AD＝8，则DE的长为( )A．2 B．3 C．4 D．5
7．如图，在△ABC中，∠B＝90°，AB＝3，AC＝5，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE的周长为____．
8．如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，将△ABC折叠，使点B恰好落在边AC上，与点B′重合，AE为折痕，则EB′＝____________．9．如图，在Rt△ABC中，∠C＝90°，BC＝6 cm，AC＝8 cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是____cm2.
11．为庆祝国庆节，某校各班都在开展丰富多彩的庆祝活动，八(1)班开展了手工制作竞赛，每个同学都在规定时间内完成一件手工作品．陈莉同学制作手工作品的前两个步骤是：①先裁下了一张长BC＝20 cm，宽AB＝16 cm的长方形纸片ABCD；②将纸片沿着直线AE折叠，点D恰好落在BC边上的F处．请你根据①②步骤计算EC，FC的长．
解：由题意得DE＝FE，AD＝AF.∵BC＝20 cm，AB＝16 cm，∴CD＝16 cm，AD＝AF＝20 cm.在Rt△ABF中，由勾股定理得BF＝12 cm，∴FC＝20－12＝8(cm).∵四边形ABCD是长方形，∴∠C＝90°.设CE＝x，则DE＝EF＝16－x，在Rt△CEF中，由勾股定理得(16－x)2＝64＋x2，解得x＝6，即EC＝6 cm
13．在一个长为2米，宽为1米的长方形草地上，如图堆放着一根长方体的木块，它的棱长和场地宽AD平行且大于AD，木块从正面看是边长为0.2米的正方形，一只蚂蚁从点A处，到达C处需要走的最短路程是______________米．
14．(黄冈中考)如图，圆柱形玻璃杯高为14 cm，底面周长为32 cm，在杯内壁离杯底5 cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿3 cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到内壁B处的最短距离为________cm.(杯壁厚度不计)
15．一位同学要用彩带装饰一个长方体礼盒．长方体高6 cm，底面是边长为4 cm的正方形，从顶点A到顶点C′如何贴彩带用彩带最短？最短长度是多少？