初中数学第五章 生活中的轴对称综合与测试习题ppt课件

这是一份初中数学第五章 生活中的轴对称综合与测试习题ppt课件，共21页。PPT课件主要包含了答案显示，见习题等内容，欢迎下载使用。

1．【2021·衡阳】在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是(　　)
2．如图，△ABC与△ADE关于直线MN对称，BC与DE的交点F在直线MN上．(1)指出图中的两对对称点；
解：对称点为B和D、C和E.
(2)指出图中相等的线段；
相等的线段有AC＝AE，AB＝AD，BC＝DE，BF＝DF，CF＝EF.
(3)指出图中其他关于直线MN对称的三角形．
解：△AFB与△AFD关于直线MN对称，△AEF与△ACF关于直线MN对称．
3．【教材P134复习题T14变式】已知：①正三角形；②正四边形；③正五边形；④正六边形；⑤正八边形……都是轴对称图形，回答下列问题：(1)数一数它们的对称轴条数，填入下表：
(2)观察上表中数据变化规律后总结，正多边形的对称轴条数与边数n有什么关系？
解：正多边形的对称轴条数与边数n相等．
(3)根据(2)，思考正二十边形有多少条对称轴．
正二十边形有20条对称轴．
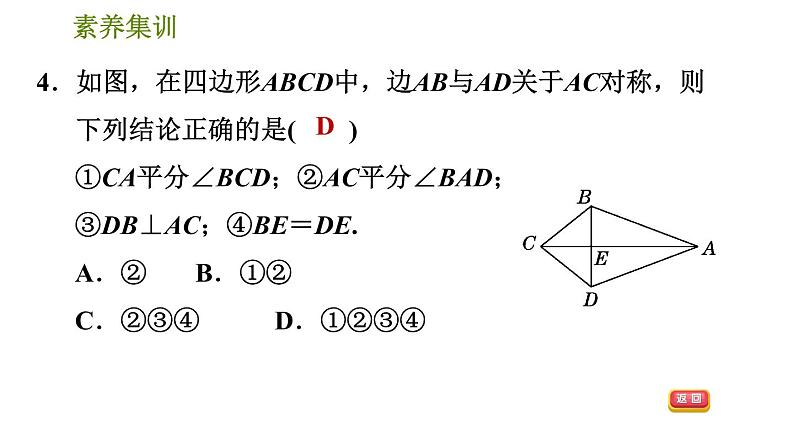
4．如图，在四边形ABCD中，边AB与AD关于AC对称，则下列结论正确的是(　　)①CA平分∠BCD；②AC平分∠BAD；③DB⊥AC；④BE＝DE.A．② B．①②C．②③④ D．①②③④
5．【教材P131复习题T4变式】如图，已知正五边形ABCDE，请用无刻度的直尺，准确作出它的一条对称轴(保留作图痕迹)．
解：答案不唯一，如：连接BD，CE，相交于点F，再过点A，F作直线，如图①所示，直线AF为所求；或者延长CB，EA，相交于点G，过点D，G作直线，如图②所示，直线GD为所求．
6．如图，在△ABC中，∠ABC＝90°，BA＝BC，过点B作直线MN.(1)画出线段BC关于直线MN成轴对称的图形BD；
解：如图所示，BD即为所求．
(2)连接AD，如果∠NBC＝25°，求∠BAD的度数．
解：如图，由题意可知BC＝BD，∠NBD＝∠NBC＝25°.又因为AB＝BC，所以AB＝BD，所以∠BAD＝∠BDA.因为∠ABD＝∠ABC＋∠CBD＝140°，所以∠BAD＋∠BDA＝40°，所以∠BAD＝20°.
7．如图，已知△ABC的边AB，BC上两点D，E，△ABE是关于直线DE对称的轴对称图形．四边形ADEC是关于直线AE对称的轴对称图形，求△ABC各内角的度数．
解：如图，因为△ABE是关于直线DE对称的轴对称图形，四边形ADEC是关于直线AE对称的轴对称图形，所以∠1＝∠B，∠1＝∠2，∠C＝∠ADE＝∠BDE.因为∠ADE＋∠BDE＝180°，所以∠ADE＝∠BDE＝90°＝∠C.又因为∠1＋∠2＋∠B＋∠C＝180°，即3∠B＝90°，所以∠B＝30°，所以∠BAC＝∠1＋∠2＝2∠B＝60°.综上所述，∠C＝90°，∠BAC＝60°，∠B＝30°.
8．如图，将长方形纸片ABCD沿EF折叠，使点A与点C重合，点D落在点G处，EF为折痕．(1)试说明：△FGC≌△EBC；
解：由题易得∠GCF＋∠FCE＝90°，∠FCE＋∠BCE＝90°，所以∠GCF＝∠BCE.又易得∠G＝∠B＝90°，GC＝BC，所以△FGC≌△EBC(ASA)．
(2)若AB＝8，AD＝4，求四边形ECGF(阴影部分)的面积．
9．阅读下题及其解题过程．已知△ABC，如图①，若点P是∠ABC和∠ACB的平分线的交点，试说明：点P到三边AB，BC，AC的距离相等．解：如图②，过点P作PD，PE，PF分别垂直于AB，BC，AC，垂足分别为D，E，F.因为BP是∠ABC的平分线，所以∠ABP＝∠CBP.
因为PE⊥BC，PD⊥AB，所以∠BDP＝∠BEP＝90°.又因为BP＝BP，所以△BPD≌△BPE(AAS)．所以PD＝PE.同理可得PE＝PF，所以PD＝PE＝PF.所以点P到三边AB，BC，AC的距离相等．
探究下列问题：(1)如图③，点E是△ABC的边BC延长线上的点，若点P是∠ABC和∠ACE的平分线的交点，上述结论还成立吗？请说明理由．
解：成立．理由如下：过点P作PD，PM，PN分别垂直于直线BA，BC，AC，垂足分别为点D，M，N，如图①所示．
因为BP是∠ABC的平分线，所以∠ABP＝∠CBP.因为PM⊥BC，PD⊥BA，所以∠BDP＝∠BMP＝90°.又因为BP＝BP，所以△BPD≌△BPM(AAS)．所以PD＝PM.同理可得PM＝PN，所以PD＝PM＝PN.所以点P到三边AB，BC，AC的距离相等．
(2)如图④，点E，F分别是△ABC的边AC，AB延长线上的点，当点P是∠CBF和∠BCE的平分线的交点时，点P到三边AB，BC，AC的距离是否相等？请说明理由．
解：点P到三边AB，BC，AC的距离相等．理由如下：过点P作PD，PM，PN分别垂直于直线AB，BC，AC，垂足分别为点D，M，N，如图②所示．