初中数学第二章 相交线与平行线综合与测试习题课件ppt

这是一份初中数学第二章 相交线与平行线综合与测试习题课件ppt，共13页。PPT课件主要包含了答案显示，见习题，答案A等内容，欢迎下载使用。

1．如图，三条直线AB，CD，EF相交于同一点O.若∠AOE＝2∠BOD，∠COF比∠AOE大30°，求∠AOC的度数．
解：设∠AOC＝x°，则∠BOD＝∠AOC＝x°.所以∠AOE＝2∠BOD＝2x°.所以∠COF＝∠AOE＋30°＝2x°＋30°.因为∠AOE＋∠AOC＋∠COF＝180°，所以2x＋x＋2x＋30＝180，解得x＝30.所以∠AOC＝30°.
2．已知OA⊥OB，OC⊥OD.(1)如图①，若∠BOC＝50°，求∠AOD的度数；
解：因为OA⊥OB，所以∠AOB＝90°.所以∠AOC＝∠AOB－∠BOC＝90°－50°＝40°.因为OC⊥OD，所以∠COD＝90°.所以∠AOD＝∠AOC＋∠COD＝40°＋90°＝130°.
(2)如图②，若∠BOC＝60°，求∠AOD的度数；
解：因为OA⊥OB，所以∠AOB＝90°.因为OC⊥OD，所以∠COD＝90°.所以∠AOD＝360°－∠AOB－∠BOC－∠COD＝360°－90°－60°－90°＝120°.
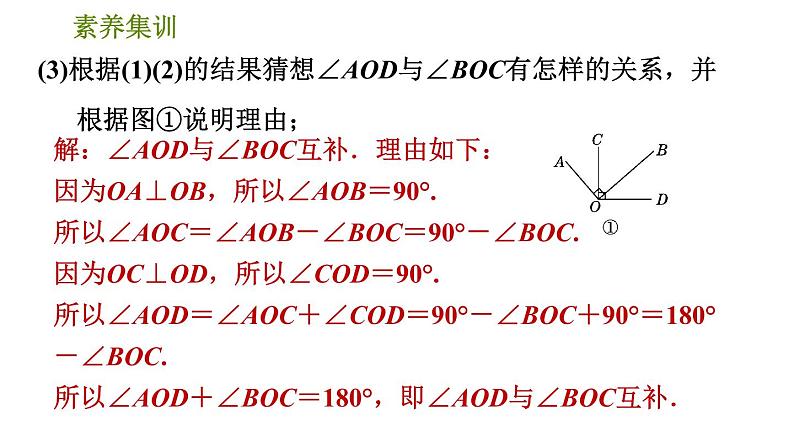
(3)根据(1)(2)的结果猜想∠AOD与∠BOC有怎样的关系，并根据图①说明理由；
解：∠AOD与∠BOC互补．理由如下：因为OA⊥OB，所以∠AOB＝90°.所以∠AOC＝∠AOB－∠BOC＝90°－∠BOC.因为OC⊥OD，所以∠COD＝90°.所以∠AOD＝∠AOC＋∠COD＝90°－∠BOC＋90°＝180°－∠BOC.所以∠AOD＋∠BOC＝180°，即∠AOD与∠BOC互补．
(4)如图②，若∠BOC∶∠AOD＝7∶29，求∠BOC和∠AOD的度数．
【点拨】如图，因为∠1＝47°，所以∠3＝90°－∠1＝90°－47°＝43°.因为∠3＋∠4＝180°，所以∠4＝180°－43°＝137°.因为直尺的两边互相平行，所以∠2＝∠4＝137°，故选D.
3．【2021·齐齐哈尔】一把直尺与一块三角尺如图放置，若∠1＝47°，则∠2的度数为(　　)A．43° B．47° C．133° D．137°
4．【中考·重庆】如图，AB∥CD，三角形EFG的顶点F，G分别落在直线AB，CD上，GE交AB于点H，GE平分∠FGD.若∠EFG＝90°，∠E＝35°，求∠EFB的度数．
解：因为在三角形EFG中，∠EFG＝90°，∠E＝35°，所以∠EGF＝180°－90°－35°＝55°.因为GE平分∠FGD，所以∠EGF＝∠EGD＝55°.因为AB∥CD，所以∠EHB＝∠EGD＝55°.又因为∠EHB＝180°－∠AHE＝∠EFB＋∠E，所以∠EFB＝∠EHB－∠E＝55°－35°＝20°.
5．【2021·随州】如图，将一块含有60°角的直角三角尺放置在两条平行线上，若∠1＝45°，则∠2为(　　)A．15° B．25° C．35° D．45°
【点拨】如图，过F作EF∥AB，所以∠EFG＝∠1＝45°.因为∠EFG＋∠EFH＝60°，所以∠EFH＝60°－∠EFG＝60°－45°＝15°.因为EF∥AB，AB∥CD，所以EF∥CD，所以∠2＝∠EFH＝15°，故选A.