初中数学人教版八年级下册17.1 勾股定理教学ppt课件

这是一份初中数学人教版八年级下册17.1 勾股定理教学ppt课件，共16页。PPT课件主要包含了教学目标，情景导入，新知探究，归纳总结，新知应用，课堂总结，LOGO，利用数轴和勾股定理等内容，欢迎下载使用。

会用勾股定理解决简单的实际问题，建立数形结合的思想。
能利用勾股定理在数轴上作出表示无理数的点。
数轴的三要素： 、 、
在数轴上表示： ， ， ，300%
我们知道数轴上的点有的表示有理数，有的表示无理数，你能在数轴上画出 吗？
分析：在数轴上找表示的点：要在数轴上画出表示的点，只要画出长为的线段即可．利用勾股定理，长为的线段是直角边为正整数2和3的直角三角形的斜边．
①在数轴上找出表示3的点A，则OA＝3，过点A作直线l垂直于OA，在l上取点B，使AB＝2；
②连接OB，以原点O为圆心，以OB为半径作弧，弧与数轴的交点C即为表示的点．
O 1 2 3
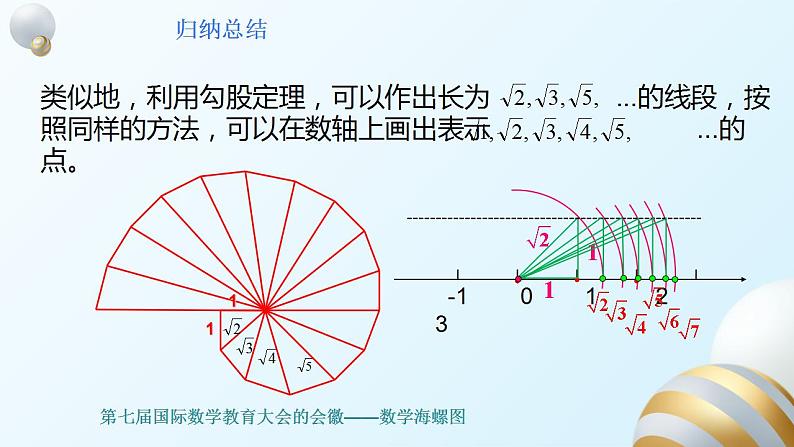
类似地，利用勾股定理，可以作出长为 ...的线段，按照同样的方法，可以在数轴上画出表示 ...的点。
-1 0 1 2 3
第七届国际数学教育大会的会徽——数学海螺图
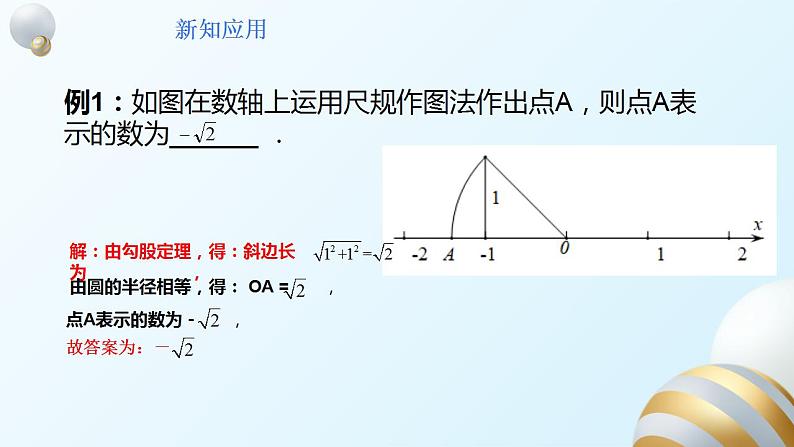
例1：如图在数轴上运用尺规作图法作出点A，则点A表示的数为______ ．
解：由勾股定理，得：斜边长为 ，
由圆的半径相等，得： OA = ，
点A表示的数为－ ，
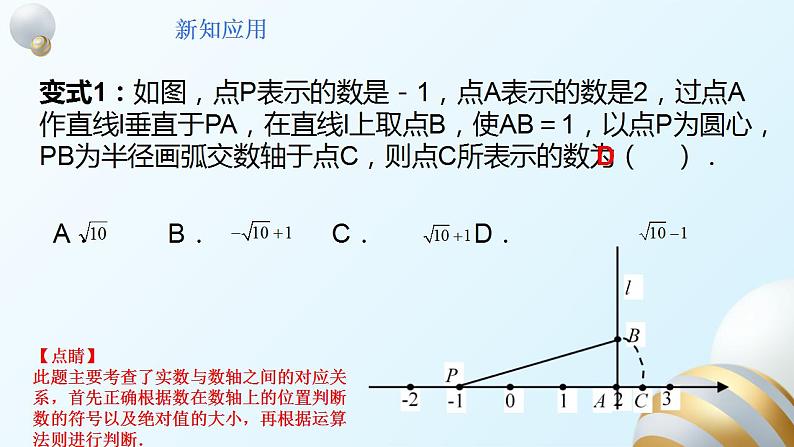
变式1：如图，点P表示的数是－1，点A表示的数是2，过点A作直线l垂直于PA，在直线l上取点B，使AB＝1，以点P为圆心，PB为半径画弧交数轴于点C，则点C所表示的数为（ ）．
A． B． C． D．
【点睛】此题主要考查了实数与数轴之间的对应关系，首先正确根据数在数轴上的位置判断数的符号以及绝对值的大小，再根据运算法则进行判断．
例2：如图（1），在4×4的方格中，每个小正方形的边长为1．
（1）求图（1）中正方形ABCD的面积；（2）如图（2），若点A在数轴上表示的数是﹣1，以A为圆心，AD为半径画圆弧与数轴的正半轴交于点E，则点E所表示的数是　 　．
（1）∵正方形ABCD边长为： ＝ ，∴正方形ABCD的面积是（ ）2＝10；（2）∵正方形ABCD边长为 ，∴AE＝AD＝ ，∴OE=AE－OA= －1，即E表示的数为 －1，故答案为： －1．
【点睛】本题考查了勾股定理、无理数在数轴上的表示方法，关键是求出正方形的边长．
变式2：如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．（1）在图1中，画一个三边长都是有理数的直角三角形；（2）在图2中，画一个以BC为斜边的直角三角形，使它们的三边长都是无理数且都不相等；（3）在图3中，画一个正方形，使它的面积是10．
解：（1）如图所示，AB=4，BC=3， ，∴ AC2=AB2+BC2 ，∴△ABC是直角三角形；
（2）如图所示， ， ，∴ AC2=AB2+BC2 ，∴△ABC是直角三角形；
【点睛】本题主要考查了有理数与无理数，正方形的判定，勾股定理和勾股定理的逆定理，熟知相关知识是解题的关键．
利用勾股定理作图或计算
构造边长为整数的直角三角形.