还剩35页未读，
继续阅读
所属成套资源：北师大版数学·必修3 PPT课件+练习+单元检测卷
成套系列资料，整套一键下载
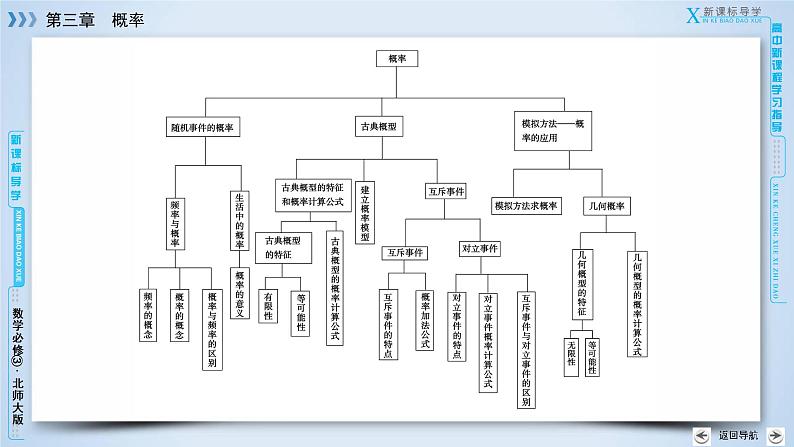
高中数学北师大版必修3第三章 概率综合与测试教学演示课件ppt
展开
这是一份高中数学北师大版必修3第三章 概率综合与测试教学演示课件ppt，共43页。PPT课件主要包含了第三章，章末归纳总结，知识结构，知识梳理，专题探究，专题二⇨古典概型，课时作业学案等内容，欢迎下载使用。
4．互斥事件(1)一般地，在一个随机试验中，我们把一次试验下不能同时发生的两个事件A和B称为互斥事件．(2)互斥事件的特征：①互斥事件研究的是两个事件之间的关系；②所研究的两个事件是在一次试验中所涉及的；③两个事件互斥是从试验的结果不能同时发生来确定的．(3)给定事件A，B，我们规定A＋B为一个事件，事件A＋B发生是指事件A和事件B至少有一个发生(推广：事件A1＋A2＋…＋An表示在一次随机试验中，A1，A2，…，An中至少有一个发生)．
解决这类问题的关键是应理清频率与概率的关系，频率是概率的估计值，是随机的，随着试验的不同而变化，而概率是多次的试验中频率的稳定值，是一个常数．不要以一次或少数次试验中的频率来估计概率．一个不透明的袋中有大小质地相同的红、白两种颜色的小球，某学习小组做摸球试验，每次从袋中摸出一个球，记下颜色后放回，搅匀后再摸．试验的部分数据如下表：
专题一 ⇨随机事件的频率与概率
(1)将表格补充完整；(所求频率保留3位小数)(2)估计从中随机摸一个球，求摸到红球的概率P.(保留2位小数)[解析] (1)第二行依次填：18,74.第三行依次填：0.200,0.278,0.258,0.253,0.250，0.252，0.248.(2)由(1)知，虽然抽取次数不同，所得频率值不同，但随试验次数的增加，频率在常数0.250附近摆动，故P≈0.25.
『规律总结』 只有当频率值在某一常数附近摆动时，才能将此常数近似看作该事件发生的概率．现实生活中很多事件的概率是难以确切得到的，鉴于随机事件的发生带有随机性的同时又存在一定的规律性，故一般通过大量的重复试验，用随机事件的频率来估计概率．
〔跟踪练习1〕 某人发现中国人在邮箱名称里喜欢用数字，于是他做了调查，结果如下表：(1)填写上表中的频率(精确到0.01)；(2)中国人的邮箱名称里使用数字的概率是多少？
[解析] (1)由频率公式可算出，表格中应填的频率从左到右依次为：0.60、0.60、0.62、0.61、0.59、0.61、0.60、0.60.(2)由(1)知，计算出的频率虽然不全相同，但都在常数0.6附近摆动，因此，中国人的邮箱名称里使用数字的概率约为0.6.
古典概型是一种最基本的概型，也是学习其他概率的基础，在高考题中，经常出现此种概率模型的题目．解题时要紧紧抓住古典概型的两个基本特征，即有限性和等可能性．另外在古典概型问题求概率时，往往需要我们将所有基本事件一一列举出来，以便确定基本事件总数及所求事件所包含的基本事件数．这就是我们常说的穷举法．在列举时应注意按一定的规律、标准，不重不漏地列举出来．
用正方体做一颗骰子，在6个面上分别标上1,2,3,4,5,6，现将这颗骰子先后抛掷两次，试问：(1)“点数之和为奇数”与“点数之和为偶数”的概率是否一样大？(2)“点数之和为6”与“点数之和为8”的概率是否一样大？(3)从问题(2)中你能发现什么样的一般规律？[思路分析] 两次点数之和的事件数比较多，可利用表格列举法来处理，分别用第一行和第一列的数表示先后掷出的点数，交叉处表示它们的和，由此可计算出所求事件的概率．
[解析] 如表格：第一行、第一列中的数表示出现的点数，行与列交叉处的数表示点数之和：
『规律总结』 涉及两次结果的问题，一般可采用表格列举法来列举基本事件，这样可保证列举时不重不漏．
〔跟踪练习2〕 一个盒子中装有4张卡片，每张卡片上写有1个数字，数字分别是1,2,3,4，现从盒子中随机抽取卡片．(1)若一次从中随机抽取3张卡片，求3张卡片上数字之和大于或等于7的概率；(2)若第一次随机抽1张卡片，放回后再随机抽取1张卡片，求两次抽取的卡片中至少一次抽到数字2的概率．
几何概型的概率公式适用于有无限多个试验结果的情况，且每种结果的出现是等可能的．试验的结果发生在一个确定的区域内，由于在确定范围内的等可能性，所以其概率等于该事件构成的子区域占总区域的比例．依这种比例求解，类似古典概型的思路，即事件A的概率由“构成事件A的基本事件所占的图形面积(长度、体积)”与“试验的全部结果所占的总面积(长度、体积)”之比来表示．
专题三 ⇨几何概型及其应用
将长为l的木棒随机折成3段，求3段长度能构成三角形的概率．[思路分析] 构成三角形要用三边长的度量，设出两边，再表示第三边．[解析] 如图所示，设A＝“3段长度能构成三角形”，x，y分别表示其中两段的长度，则第3段的长度为l－x－y.
『规律总结』 一般地，若一个随机事件需要用两个连续变量[如本例中的(x，y)]来描述，用这两个变量的有序实数对来表示它的基本事件，利用坐标平面能顺利地建立与面积有关的几何概型．
互斥事件和对立事件，都是研究怎样从一些简单的事件的概率的计算来推算较复杂事件的概率，应用互斥事件的概率的加法公式解题，备受高考命题者的青睐，应用公式时一定要注意首先确定各个事件是否彼此互斥，然后求出各事件分别发生的概率，再求和．对于较复杂事件的概率，可以转化为求对立事件的概率，下面举例说明．
专题四 ⇨互斥事件、对立事件
黄种人群中各种血型的人所占的比例如下：已知同种血型的人可以输血，O型血可以输给任一种血型的人，其他不同血型的人不能互相输血，小明是B型血，若小明因病需要输血，求：(1)任找一个人，其血可以输给小明的概率；(2)任找一个人，其血不能输给小明的概率．
[解析] (1)对任一个人，其血为A，B，AB，O型血的事件分别为A′，B′，C′，D′，它们是互斥的，由已知条件得：P(A′)＝0.28，P(B′)＝0.29，P(C′)＝0.08，P(D′)＝0.35.因为B，O型血可以输给B型血的人，故“可以输给B型血的人” 为事件B′＋D′，根据互斥事件的概率加法公式，有：P(B′＋D′)＝P(B′)＋P(D′)＝0.29＋0.35＝0.64.故任找一个人，其血可以输给小明的概率是0.64.(2)由于A，AB型血不能输给B型血的人，故“不能输出B型血的人”为事件A′＋C′，且A′与C′为互斥事件，有：P(A′＋C′)＝P(A′)＋P(C′)＝0.28＋0.08＝0.36.故任找一个人，其血不能输给小明的概率为0.36.
『规律总结』 本题既可以使用互斥事件的加法公式求解，也可以使用对立事件的公式求解．对于第(2)问也可以这样解答：因为事件“其血型可以输给B型血的人”与事件“其血型不能输给B型血的人”是对立事件，故由对立事件的概率公式为：P(A′＋C′)＝1－P(B′＋D′)＝1－0.64＝0.36.
〔跟踪练习4〕 据统计，某储蓄所一个窗口等候的人数及相应的概率如下：(1)至多2人排队等候的概率是多少？(2)至少3人排队等候的概率是多少？[解析] 记在窗口等候的人数为0、1、2分别为事件A、B、C，则A、B、C彼此互斥．(1)至多2人排队等候的概率是P(A∪B∪C)＝P(A)＋P(B)＋P(C)＝0.1＋0.16＋0.3＝0.56.(2)至少3人排队等候的概率是：1－P(A∪B∪C)＝1－0.56＝0.44.
某初级中学共有学生2 000名，各年级男、女生人数如下表：已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.(1)求x的值；(2)现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？(3)已知y≥245，z≥245，求初三年级中女生比男生多的概率．
专题五 ⇨概率与其他知识的综合应用
(3)当y≥245，z≥245时，初三年级中男、女生人数的所有可能组合为：
〔跟踪练习5〕 国家统计局发布最新数据显示，2013年11月份全国副省级城市中CPI(消费物价指数)值位于前15位的城市具体情况如下表：
(1)求这15个城市CPI值的平均值及众数；(2)完成下表：(3)从区间[103.0,104.0)上随机选取2个城市，求恰有1个城市CPI值在区间[103.5,104.0)上的概率．
4．互斥事件(1)一般地，在一个随机试验中，我们把一次试验下不能同时发生的两个事件A和B称为互斥事件．(2)互斥事件的特征：①互斥事件研究的是两个事件之间的关系；②所研究的两个事件是在一次试验中所涉及的；③两个事件互斥是从试验的结果不能同时发生来确定的．(3)给定事件A，B，我们规定A＋B为一个事件，事件A＋B发生是指事件A和事件B至少有一个发生(推广：事件A1＋A2＋…＋An表示在一次随机试验中，A1，A2，…，An中至少有一个发生)．
解决这类问题的关键是应理清频率与概率的关系，频率是概率的估计值，是随机的，随着试验的不同而变化，而概率是多次的试验中频率的稳定值，是一个常数．不要以一次或少数次试验中的频率来估计概率．一个不透明的袋中有大小质地相同的红、白两种颜色的小球，某学习小组做摸球试验，每次从袋中摸出一个球，记下颜色后放回，搅匀后再摸．试验的部分数据如下表：
专题一 ⇨随机事件的频率与概率
(1)将表格补充完整；(所求频率保留3位小数)(2)估计从中随机摸一个球，求摸到红球的概率P.(保留2位小数)[解析] (1)第二行依次填：18,74.第三行依次填：0.200,0.278,0.258,0.253,0.250，0.252，0.248.(2)由(1)知，虽然抽取次数不同，所得频率值不同，但随试验次数的增加，频率在常数0.250附近摆动，故P≈0.25.
『规律总结』 只有当频率值在某一常数附近摆动时，才能将此常数近似看作该事件发生的概率．现实生活中很多事件的概率是难以确切得到的，鉴于随机事件的发生带有随机性的同时又存在一定的规律性，故一般通过大量的重复试验，用随机事件的频率来估计概率．
〔跟踪练习1〕 某人发现中国人在邮箱名称里喜欢用数字，于是他做了调查，结果如下表：(1)填写上表中的频率(精确到0.01)；(2)中国人的邮箱名称里使用数字的概率是多少？
[解析] (1)由频率公式可算出，表格中应填的频率从左到右依次为：0.60、0.60、0.62、0.61、0.59、0.61、0.60、0.60.(2)由(1)知，计算出的频率虽然不全相同，但都在常数0.6附近摆动，因此，中国人的邮箱名称里使用数字的概率约为0.6.
古典概型是一种最基本的概型，也是学习其他概率的基础，在高考题中，经常出现此种概率模型的题目．解题时要紧紧抓住古典概型的两个基本特征，即有限性和等可能性．另外在古典概型问题求概率时，往往需要我们将所有基本事件一一列举出来，以便确定基本事件总数及所求事件所包含的基本事件数．这就是我们常说的穷举法．在列举时应注意按一定的规律、标准，不重不漏地列举出来．
用正方体做一颗骰子，在6个面上分别标上1,2,3,4,5,6，现将这颗骰子先后抛掷两次，试问：(1)“点数之和为奇数”与“点数之和为偶数”的概率是否一样大？(2)“点数之和为6”与“点数之和为8”的概率是否一样大？(3)从问题(2)中你能发现什么样的一般规律？[思路分析] 两次点数之和的事件数比较多，可利用表格列举法来处理，分别用第一行和第一列的数表示先后掷出的点数，交叉处表示它们的和，由此可计算出所求事件的概率．
[解析] 如表格：第一行、第一列中的数表示出现的点数，行与列交叉处的数表示点数之和：
『规律总结』 涉及两次结果的问题，一般可采用表格列举法来列举基本事件，这样可保证列举时不重不漏．
〔跟踪练习2〕 一个盒子中装有4张卡片，每张卡片上写有1个数字，数字分别是1,2,3,4，现从盒子中随机抽取卡片．(1)若一次从中随机抽取3张卡片，求3张卡片上数字之和大于或等于7的概率；(2)若第一次随机抽1张卡片，放回后再随机抽取1张卡片，求两次抽取的卡片中至少一次抽到数字2的概率．
几何概型的概率公式适用于有无限多个试验结果的情况，且每种结果的出现是等可能的．试验的结果发生在一个确定的区域内，由于在确定范围内的等可能性，所以其概率等于该事件构成的子区域占总区域的比例．依这种比例求解，类似古典概型的思路，即事件A的概率由“构成事件A的基本事件所占的图形面积(长度、体积)”与“试验的全部结果所占的总面积(长度、体积)”之比来表示．
专题三 ⇨几何概型及其应用
将长为l的木棒随机折成3段，求3段长度能构成三角形的概率．[思路分析] 构成三角形要用三边长的度量，设出两边，再表示第三边．[解析] 如图所示，设A＝“3段长度能构成三角形”，x，y分别表示其中两段的长度，则第3段的长度为l－x－y.
『规律总结』 一般地，若一个随机事件需要用两个连续变量[如本例中的(x，y)]来描述，用这两个变量的有序实数对来表示它的基本事件，利用坐标平面能顺利地建立与面积有关的几何概型．
互斥事件和对立事件，都是研究怎样从一些简单的事件的概率的计算来推算较复杂事件的概率，应用互斥事件的概率的加法公式解题，备受高考命题者的青睐，应用公式时一定要注意首先确定各个事件是否彼此互斥，然后求出各事件分别发生的概率，再求和．对于较复杂事件的概率，可以转化为求对立事件的概率，下面举例说明．
专题四 ⇨互斥事件、对立事件
黄种人群中各种血型的人所占的比例如下：已知同种血型的人可以输血，O型血可以输给任一种血型的人，其他不同血型的人不能互相输血，小明是B型血，若小明因病需要输血，求：(1)任找一个人，其血可以输给小明的概率；(2)任找一个人，其血不能输给小明的概率．
[解析] (1)对任一个人，其血为A，B，AB，O型血的事件分别为A′，B′，C′，D′，它们是互斥的，由已知条件得：P(A′)＝0.28，P(B′)＝0.29，P(C′)＝0.08，P(D′)＝0.35.因为B，O型血可以输给B型血的人，故“可以输给B型血的人” 为事件B′＋D′，根据互斥事件的概率加法公式，有：P(B′＋D′)＝P(B′)＋P(D′)＝0.29＋0.35＝0.64.故任找一个人，其血可以输给小明的概率是0.64.(2)由于A，AB型血不能输给B型血的人，故“不能输出B型血的人”为事件A′＋C′，且A′与C′为互斥事件，有：P(A′＋C′)＝P(A′)＋P(C′)＝0.28＋0.08＝0.36.故任找一个人，其血不能输给小明的概率为0.36.
『规律总结』 本题既可以使用互斥事件的加法公式求解，也可以使用对立事件的公式求解．对于第(2)问也可以这样解答：因为事件“其血型可以输给B型血的人”与事件“其血型不能输给B型血的人”是对立事件，故由对立事件的概率公式为：P(A′＋C′)＝1－P(B′＋D′)＝1－0.64＝0.36.
〔跟踪练习4〕 据统计，某储蓄所一个窗口等候的人数及相应的概率如下：(1)至多2人排队等候的概率是多少？(2)至少3人排队等候的概率是多少？[解析] 记在窗口等候的人数为0、1、2分别为事件A、B、C，则A、B、C彼此互斥．(1)至多2人排队等候的概率是P(A∪B∪C)＝P(A)＋P(B)＋P(C)＝0.1＋0.16＋0.3＝0.56.(2)至少3人排队等候的概率是：1－P(A∪B∪C)＝1－0.56＝0.44.
某初级中学共有学生2 000名，各年级男、女生人数如下表：已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.(1)求x的值；(2)现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？(3)已知y≥245，z≥245，求初三年级中女生比男生多的概率．
专题五 ⇨概率与其他知识的综合应用
(3)当y≥245，z≥245时，初三年级中男、女生人数的所有可能组合为：
〔跟踪练习5〕 国家统计局发布最新数据显示，2013年11月份全国副省级城市中CPI(消费物价指数)值位于前15位的城市具体情况如下表：
(1)求这15个城市CPI值的平均值及众数；(2)完成下表：(3)从区间[103.0,104.0)上随机选取2个城市，求恰有1个城市CPI值在区间[103.5,104.0)上的概率．
相关课件
高中数学第一章 统计综合与测试课文配套ppt课件： 这是一份高中数学第一章 统计综合与测试课文配套ppt课件，共8页。
高中数学北师大版必修3第一章 统计综合与测试教课内容课件ppt： 这是一份高中数学北师大版必修3第一章 统计综合与测试教课内容课件ppt，共60页。PPT课件主要包含了第一章，章末归纳总结，知识结构，知识梳理，专题探究，专题三⇨统计图表，2把数据列成表，课时作业学案等内容，欢迎下载使用。
高中北师大版第三章 三角恒等变换综合与测试教学演示课件ppt： 这是一份高中北师大版第三章 三角恒等变换综合与测试教学演示课件ppt，共51页。PPT课件主要包含了第三章，三角恒等变形，章末整合提升，知识结构，知识梳理，专题探究，典例1，典例2，专题三⇨求角的大小，典例3等内容，欢迎下载使用。
