2021年北京海淀区五十七中九年级上期末数学试卷

这是一份2021年北京海淀区五十七中九年级上期末数学试卷，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 德育处王主任将 10 份奖品分别放在 10 个完全相同的不透明礼盒中，准备将它们奖给小明等 10 位获“科技节活动先进个人”称号的同学．这些奖品中有 5 份是学习文具，3 份是科普读物，2 份是科技馆通票．小明同学从中随机取一份奖品，恰好取到科普读物的概率是
A. 12B. 35C. 15D. 310

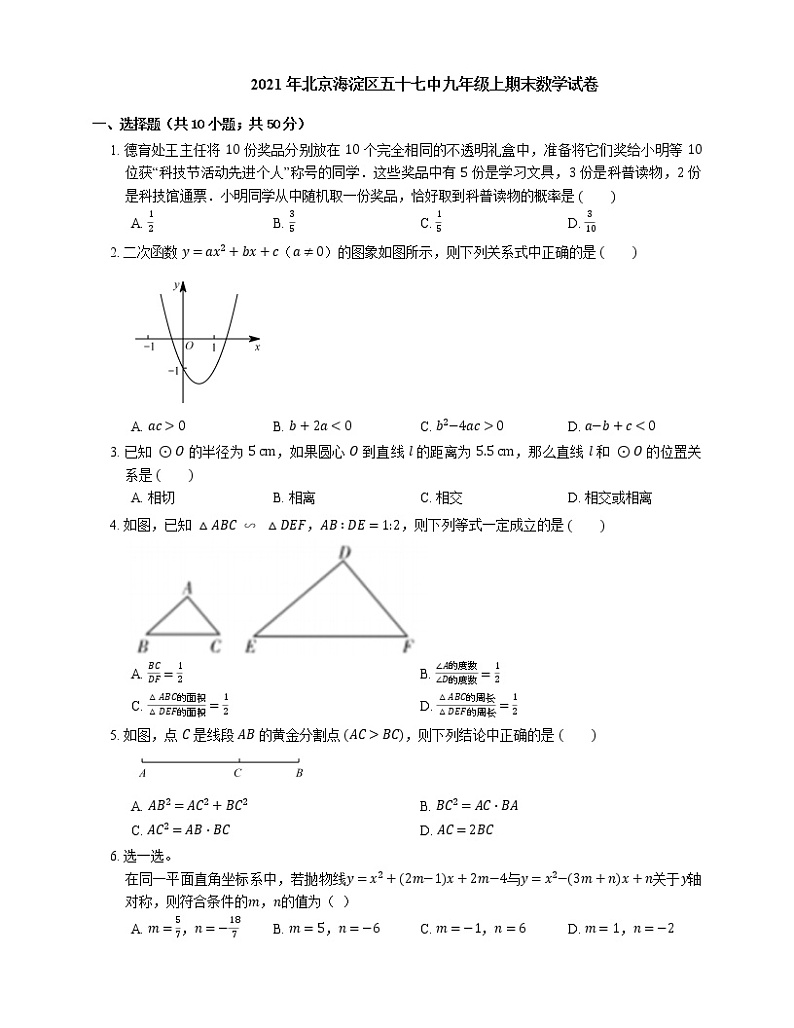
2. 二次函数 y=ax2+bx+c（a≠0）的图象如图所示，则下列关系式中正确的是
A. ac>0B. b+2a<0C. b2−4ac>0D. a−b+c<0

3. 已知 ⊙O 的半径为 5 cm，如果圆心 O 到直线 l 的距离为 5.5 cm，那么直线 l 和 ⊙O 的位置关系是
A. 相切B. 相离C. 相交D. 相交或相离

4. 如图，已知 △ABC∽△DEF，AB∶DE=1:2，则下列等式一定成立的是
A. BCDF=12B. ∠A的度数∠D的度数=12
C. △ABC的面积△DEF的面积=12D. △ABC的周长△DEF的周长=12

5. 如图，点 C 是线段 AB 的黄金分割点 AC>BC，则下列结论中正确的是
A. AB2=AC2+BC2B. BC2=AC⋅BA
C. AC2=AB⋅BCD. AC=2BC

6. 选一选。
在同一平面直角坐标系中，若抛物线y=x2+(2m−1)x+2m−4与y=x2−(3m+n)x+n关于y轴对称，则符合条件的m，n的值为（ ）
A. m=57，n=−187B. m=5，n=−6C. m=−1，n=6D. m=1，n=−2

7. 如图，一个三角尺 ABC 的斜边 AB 与量角器的直径恰好重合，点 D 对应的刻度是 46∘，则 ∠ACD 的度数为
A. 46∘B. 23∘C. 44∘D. 67∘

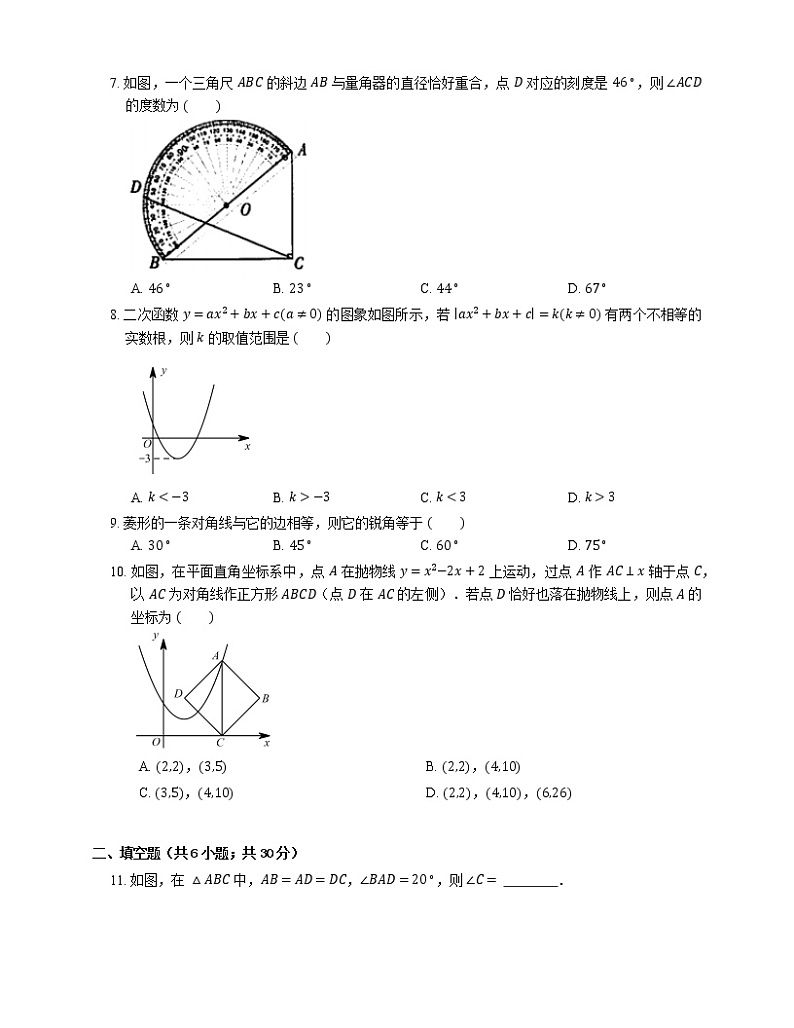
8. 二次函数 y=ax2+bx+ca≠0 的图象如图所示，若 ax2+bx+c=kk≠0 有两个不相等的实数根，则 k 的取值范围是
A. k<−3B. k>−3C. k<3D. k>3

9. 菱形的一条对角线与它的边相等，则它的锐角等于
A. 30∘B. 45∘C. 60∘D. 75∘

10. 如图，在平面直角坐标系中，点 A 在抛物线 y=x2−2x+2 上运动，过点 A 作 AC⊥x 轴于点 C，以 AC 为对角线作正方形 ABCD（点 D 在 AC 的左侧）．若点 D 恰好也落在抛物线上，则点 A 的坐标为
A. 2,2，3,5B. 2,2，4,10
C. 3,5，4,10D. 2,2，4,10，6,26

二、填空题（共6小题；共30分）
11. 如图，在 △ABC 中，AB=AD=DC，∠BAD=20∘，则 ∠C= ．

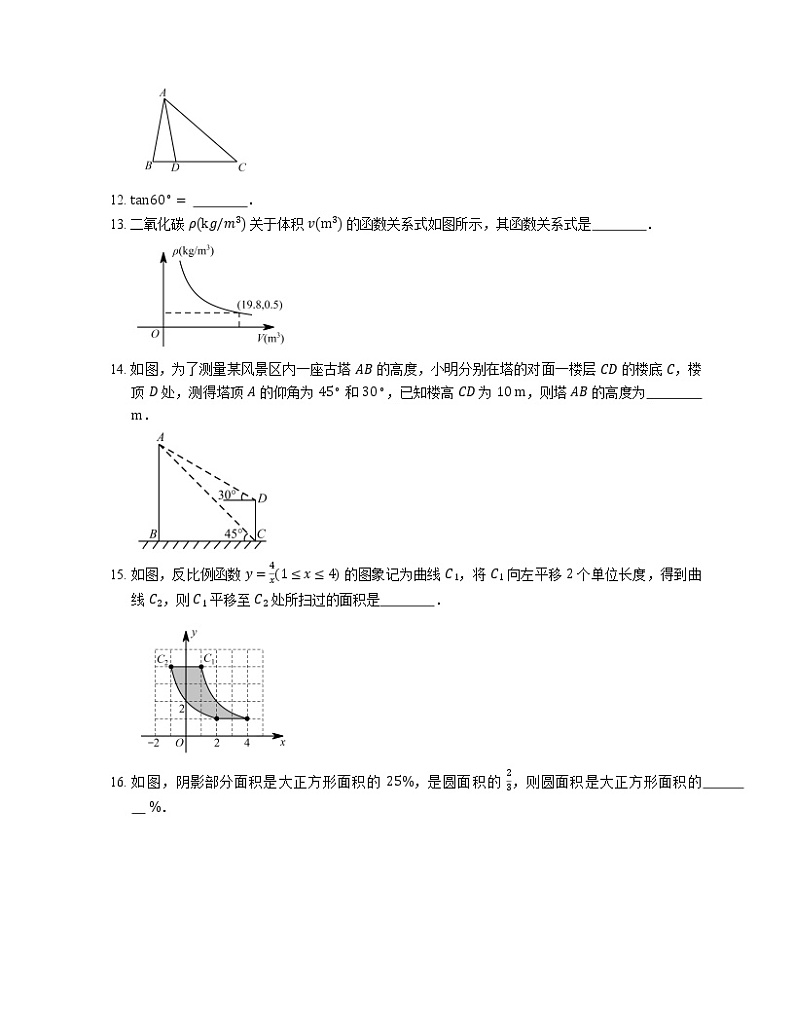
12. tan60∘= ．

13. 二氧化碳 ρkg/m3 关于体积 vm3 的函数关系式如图所示，其函数关系式是 ．

14. 如图，为了测量某风景区内一座古塔 AB 的高度，小明分别在塔的对面一楼层 CD 的楼底 C，楼顶 D 处，测得塔顶 A 的仰角为 45∘ 和 30∘，已知楼高 CD 为 10 m，则塔 AB 的高度为 m．

15. 如图，反比例函数 y=4x1≤x≤4 的图象记为曲线 C1，将 C1 向左平移 2 个单位长度，得到曲线 C2，则 C1 平移至 C2 处所扫过的面积是 ．

16. 如图，阴影部分面积是大正方形面积的 25%，是圆面积的 23，则圆面积是大正方形面积的 %．

三、解答题（共13小题；共169分）
17. 在正方形 ABCD 中，DE 为正方形的外角 ∠ADF 的平分线，点 G 在线段 AD 上，过点 G 作 PG⊥DE 于点 P，连接 CP，过点 D 作 DQ⊥PC 于点 Q，交射线 PG 于点 H．
（1）如图 1，若点 G 与点 A 重合．
①依题意补全图 1；
②判断 DH 与 PC 的数量关系并加以证明；
（2）如图 2，若点 H 恰好在线段 AB 上，正方形 ABCD 的边长为 1，请写出求 DP 长的思路（可以不写出计算结果）．

18. 计算
（1）2sin30∘−12+tan60∘．
（2）sin260∘+∣tan45∘−2∣−2cs45∘．

19. 已知抛物线 y=−x2+bx+c 经过点 A3,0，B−1,0．
（1）求抛物线的解析式；
（2）求抛物线的顶点坐标．

20. 如图，⊙O 是输水管的切面，阴影部分是有水部分，其中水面 AB 宽 10 cm，水最深的地方深 3 cm，求输水管的半径．

21. 某校学生会正筹备一个“庆毕业”文艺汇演活动，现准备从 4 名（其中两男两女）节目主持候选人中，随机选取两人担任节目主持人，请用列表法或画树状图求选出的两名主持人“恰好为一男一女”的概率．

22. 如图，在 △ABC 中，∠B=45∘，∠C=75∘，夹边 BC 的长为 6，求 △ABC 的面积．

23. 如图，Rt△ABC 的斜边 AC 的两个顶点在反比例函数 y=k1x 的图象上，点 B 在反比例函数 y=k2x 的图象上，AB 与 x 轴平行，BC=2，点 A 的坐标为 1,3．
（1）求 C 点的坐标．
（2）求点 B 所在函数图象的解析式．

24. 某校数学活动课上，开展测量学校教学大楼 AB 高度的实践活动，三个小组设计了不同方案，测量数据如下表：
（1）根据测量方案和所得数据，第 组的数据无法算出大楼高度?
（2）请选择其中一个可行方案及其测量数据，求出教学大楼的高度．
参考数据：sin37∘≈0.60，cs37∘≈0.80，tan37∘≈0.75．

25. 某大型超市将进价为 40 元的某种服装按 50 元售出时，每天可以售出 300 套．据市场调查发现，这种服装每提高 1 元，销售量就减少 5 套，如果超市将售价定为 x 元．请你求出每天销售利润 y 元与售价 x 元的函数表达式．

26. 已知在 △ABC 中，∠A:∠B:∠C=1:2:3，c−b=4−23．解这个三角形．

27. 抛物线 y=ax2+bx+ca≠0 上部分点的横坐标 x，纵坐标 y 的对应值如表：
x⋯−2−10123⋯y⋯046640⋯
（1）求这个二次函数的表达式；
（2）直接写出当 y<0 时 x 的取值范围．

28. 如图，AB 是 ⊙O 的直径，弦 CD⊥AB 于点 E，在 ⊙O 的切线 CM 上取一点 P，使得 ∠CPB=∠COA．
（1）求证：PB 是 ⊙O 的切线；
（2）若 AB=43，CD=6，求 PB 的长．

29. 如图，一次函数 y=−23x+2 的图象分别与 x 轴，y 轴交于点 A，B，以线段 AB 为边在第一象限内作等腰 Rt△ABC，∠BAC=90∘．
（1）求点 A，B 的坐标；
（2）求过 B，C 两点的直线的解析式．
答案
第一部分
1. D【解析】小明同学从中随机取一份奖品，恰好取到科普读物的概率是 310．
2. C【解析】A、由函数图象可知二次函数 y=ax2+bx+c 的开口向上，即 a>0，交于 y 轴的负半轴，c<0，ac<0，故本选项错误；
B、由函数图象可知对称轴为直线 x=−b2a<1，所以 −b<2a，即 2a+b>0，故本选项错误；
C、由函数图象可知二次函数 y=ax2+bx+c 与 x 轴有两个交点，则 b2−4ac>0．故本选项正确；
D、由函数图象可知当 x=−1 时，y>0，a−b+c>0，故本选项错误．
3. B
4. B【解析】根据相似三角形的性质，对应边的比等于相似比，BC 与 DF 不是对应边，排除A选项；对应角相等，排除B选项；面积比等于相似比的平方，排除C选项；周长比等于相似比，则D选项正确．
5. C
6. D【解析】∵抛物线y=x2+(2m−1)x+2m−4与y=x2−(3m+n)x+n关于y轴对称，
∴
2m−1=3m+n2m−4=n
，解之得
m=1n=−2
，
故选：D．
7. D【解析】如图，连接 OD，
∵ 三角尺 ABC 的斜边 AB 与量角器的直径恰好重合，
∴A，B，C，D 四点共圆，
∵ 点 D 对应的刻度是 46∘，
∴∠BOD=46∘，
∴∠BCD=12∠BOD=23∘，
∴∠ACD=90∘−∠BCD=67∘．
8. D
9. C
10. B
第二部分
11. 40∘
【解析】∵AB=AD，∠BAD=20∘，
∴∠B=12180∘−∠BAD=12180∘−20∘=80∘．
∵∠ADC 是 △ABD 的外角，
∴∠ADC=∠B+∠BAD=80∘+20∘=100∘．
∵AD=DC．
∴∠C=12180∘−∠ADC=12180∘−100∘=40∘．
12. 3
13. ρ=9.9v
14. 15+53
15. 6
【解析】如图所示，C1 平移至 C2 处所扫过的面积是 2×3=6．
16. 37.5
第三部分
17. （1） ①依题意补全图 1，如图 1 所示：
② DH=PC，理由如下：
∵DE 为正方形的外角 ∠ADF 的平分线，
∴∠EDF=∠ADE=45∘，
∴∠PDC=135∘，
∵PG⊥DE 于点 P，
∴∠DAP=45∘，
∴∠HAD=135∘，
∴∠HAD=∠PDC，
∵ 四边形 ABCD 为正方形，
∴AD=CD，
∵DQ⊥PC，
∴∠CDQ+∠DCQ=90∘，
∵∠ADQ+∠CDQ=90∘，
∴∠ADQ=∠DCQ，
在 △HAD 和 △PDC 中，
∠HAD=∠PDC,AD=DC,∠ADQ=∠DCQ,
∴△HAD≌△PDC，
∴DH=CP．
（2） 求 DP 长的思路如下：如图 2 所示：
a、与②同理得：∠HGD=∠PDC，∠ADQ=∠DCP，
∴△HGD∽△PDC；
b 、由②可知 △GPD 为等腰直角三角形，
∴∠AGH=∠PGD=45∘，
∴△AGH 为等腰直角三角形，
设 DP=PG=x，则 GD=2x，AG=1−2x，GH=2−2x；
c 、由 △HGD∽△PDC 得：GHDP=GDDC，
即 2−2xx=2x1，
解得：x=−2±62（负值舍去），
∴DP=6−22．
18. （1） 原式= 2×12−23+3，
= 1−3．
（2） 原式= 322+∣1−2∣−2×22，
= −14．
19. （1） ∵ 抛物线 y=−x2+bx+c 经过点 A3,0，B−1,0，
∴ 抛物线的解析式为 y=−x−3x+1，
即 y=−x2+2x+3．
（2） ∵y=−x2+2x+3=−x−12+4，
∴ 抛物线的顶点坐标为 1,4．
20. 如答图，过点 O 作 OD⊥AB 于点 D，交 ⊙O 于点 E，
则 AD=BD=12AB=5，DE=3．
设输水管的半径为 r，则 OD=r−3．
在 Rt△OBD 中，OB2=BD2+OD2，即 r2=52+r−32．
解得 r=173．
∴ 输水管的半径为 173 cm．
21. 列表如下：
男男女女男−−−男,男女,男女,男男男,男−−−女,男女,男女男,女男,女−−−女,女女男,女男,女女,女−−−
所有等可能的情况有 12 种，其中选出的两名主持人“恰好为一男一女”的情况有 8 种，则 P （ 选出的两名主持人
“恰好为一男一女”） =812=23 .
22. 如图，作 CD⊥AB 于点 D，
在 Rt△BCD 中，CD=BC⋅sinB=6×22=32，
BD=BC⋅csB=6×22=32，
∴CD=BD，
∴∠BCD=∠B=45∘，
在 Rt△ACD 中，∠ACD=75∘−45∘=30∘，
∴tan30∘=ADCD，
∴AD=32×33=6，
∴S△ABC=12×32+6×32=9+33．
23. （1） 把点 A1,3 代入反比例函数 y=k1x 得 k1=1×3=3，
∴ 过 A 点与 C 点的反比例函数解析式为 y=3x，
∵AB 与 x 轴平行，
∴B 点的纵坐标为 3，
∵BC 平行 y 轴，BC=2，
∴C 点的纵坐标为 1，
把 y=1 代入 y=3x 得 x=3，
∴C 点坐标为 3,1．
（2） 把 B3,3 代入反比例函数 y=k2x 得 k2=3×3=9，
∴ 点 B 所在函数图象的解析式为 y=9x．
24. （1） 二
（2） 第一组：
在 Rt△ABD 中，AB⊥BC，由 ∠ADB=45∘，
得 AB=BD．
设 AB=BD=x，则 BC=12+x，
在 Rt△ABC 中，由 ∠C=37∘，
tan∠C=ABBC，
得 xx+12=34．
解得 x=36．
答：教学大楼的高度是 36 米．
第三组：
在 Rt△ABF 中，AB⊥BP，由 ∠AFB=45∘，
得 AB=BF．
在 Rt△PEF 中，由 EF=9，∠P=37∘，
得 PF=12，
设 AB=BF=x，则 BP=12+x．
在 Rt△PAB 中，由 ∠P=37∘，tan∠P=ABBP，
得 xx+12=34．
解得 x=36．
答：教学大楼的高度是 36 米．
25. y=x−40300−x−50×5=−5x2+750x−22000.
26. ∵∠A:∠B:∠C=1:2:3，
∴∠A=180∘×11+2+3=30∘，∠B=60∘，∠C=90∘．
∴sinB=sin60∘=bc=32．
∴b=32c．
∵c−b=4−23，
∴c−32c=4−23，
解得 c=4．
则 b=23，a=42−232=2．
27. （1） 设抛物线的表达式为：y=ax+2x−3，
把 0,6 代入得：6=−6a，a=−1，
所以抛物线的表达式为：y=−x+2x−3=−x2+x+6；
（2） 如图所示，
由图象得：当 y<0 时，x 的取值范围是：x<−2 或 x>3．
28. （1） ∵PC 与 ⊙O 相切于点 C，
∴OC⊥PC．
∴∠OCP=90∘．
∵∠AOC=∠CPB，∠AOC+∠BOC=180∘，
∴∠BOC+∠CPB=180∘．
在四边形 PBOC 中，∠PBO=360∘−∠CPB−∠BOC−∠PCO=90∘．
∴ 半径 OB⊥PB．
∴PB 是 ⊙O 的切线．
（2） 解法 1：
连接 OP，如图．
∵AB 是 ⊙O 的直径，AB=43，
∴OC=OB=12AB=23．
∵ 弦 CD⊥AB 于点 E，CD=6，
∴CE=12CD=3．
在 Rt△CEO 中，sin∠COE=CECO=32．
∴∠COE=60∘．
∵PB，PC 都是 ⊙O 的切线，
∴∠CPO=∠BPO，∠OCP=∠OBP．
∴∠COP=∠BOP=60∘．
∴PB=OB⋅tan60∘=6．
【解析】解法 2：
连接 BC，如图．
∵AB 是 ⊙O 的直径，AB=43，
∴OC=12AB=23，
∵ 弦 CD⊥AB 于点 E，CD=6，
∴CE=12CD=3．
在 Rt△CEO 中，sin∠COE=CECO=32，
∴∠COE=60∘，
∴∠CPB=∠COE=60∘，∠ABC=12∠COE=30∘．
∴BC=2CE=6．
∵PB，PC 都是 ⊙O 的切线，
∴PB=PC．
∴△PBC 为等边三角形．
∴PB=BC=6．
29. （1） ∵ 一次函数 y=−23x+2 中，
令 x=0 得：y=2；
令 y=0，解得 x=3，
∴B 的坐标是 0,2，A 的坐标是 3,0．
（2） 如图，作 CD⊥x 轴于点 D．
∵∠BAC=90∘，
∴∠OAB+∠CAD=90∘．
又 ∵∠CAD+∠ACD=90∘，
∴∠ACD=∠BAO．
在 △ABO 与 △CAD 中，
∠BAO=∠ACD,∠BOA=∠ADC,AB=CA,
∴△ABO≌△CAD（AAS）．
∴OB=AD=2，OA=CD=3，OD=OA+AD=5．
则 C 的坐标是 5,3，
设直线 BC 的解析式是 y=kx+b，
根据题意得：5k+b=3,b=2,
解得：k=15，b=2，
∴ 直线 BC 的解析式是 y=15x+2．