2021年北京丰台区北大附属实验学校八年级下期末数学试卷

这是一份2021年北京丰台区北大附属实验学校八年级下期末数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共10小题；共50分）
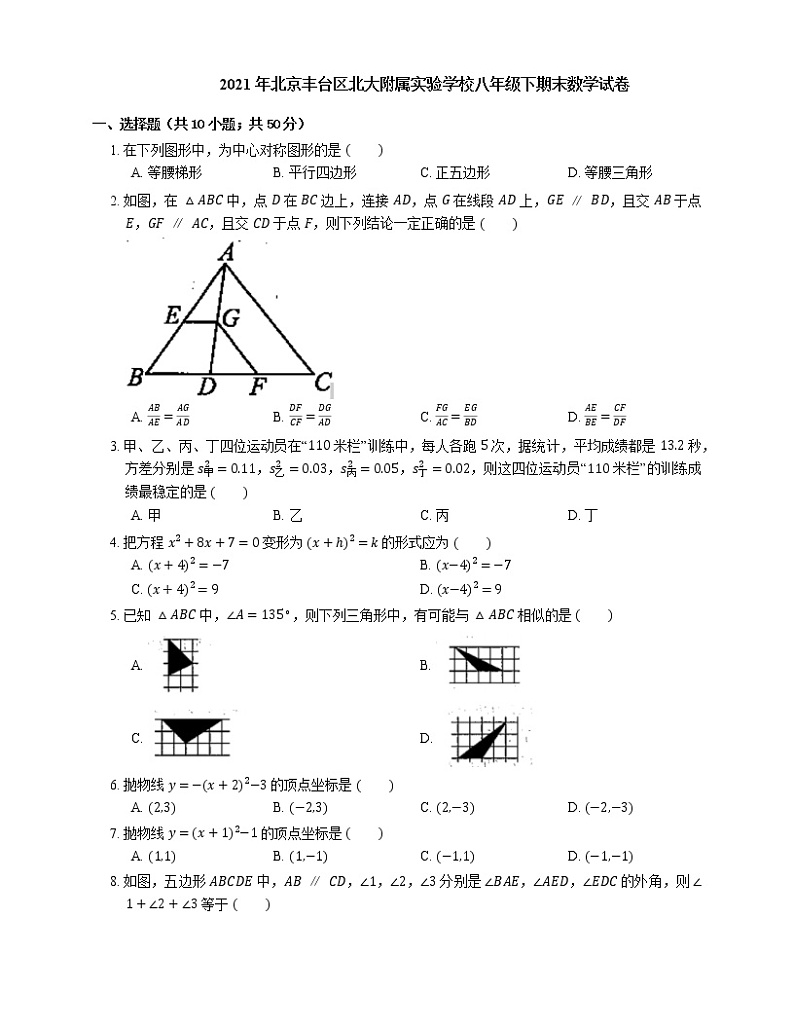
1. 在下列图形中，为中心对称图形的是
A. 等腰梯形B. 平行四边形C. 正五边形D. 等腰三角形

2. 如图，在 △ABC 中，点 D 在 BC 边上，连接 AD，点 G 在线段 AD 上，GE∥BD，且交 AB 于点 E，GF∥AC，且交 CD 于点 F，则下列结论一定正确的是
A. ABAE=AGADB. DFCF=DGADC. FGAC=EGBDD. AEBE=CFDF

3. 甲、乙、丙、丁四位运动员在“110 米栏”训练中，每人各跑 5 次，据统计，平均成绩都是 13.2 秒，方差分别是 s甲2=0.11，s乙2=0.03，s丙2=0.05，s丁2=0.02，则这四位运动员“110 米栏”的训练成绩最稳定的是
A. 甲B. 乙C. 丙D. 丁

4. 把方程 x2+8x+7=0 变形为 x+h2=k 的形式应为
A. x+42=−7B. x−42=−7
C. x+42=9D. x−42=9

5. 已知 △ABC 中，∠A=135∘，则下列三角形中，有可能与 △ABC 相似的是
A. B.
C. D.

6. 抛物线 y=−x+22−3 的顶点坐标是
A. 2,3B. −2,3C. 2,−3D. −2,−3

7. 抛物线 y=x+12−1 的顶点坐标是
A. 1,1B. 1,−1C. −1,1D. −1,−1

8. 如图，五边形 ABCDE 中，AB∥CD，∠1，∠2，∠3 分别是 ∠BAE，∠AED，∠EDC 的外角，则 ∠1+∠2+∠3 等于
A. 90∘B. 180∘C. 210∘D. 270∘

9. 如图，在正方形 ABCD 中，E 为 AD 上的中点，P 为 AB 上的一个动点，若 AB=2，则 PE+PC 的最小值为
A. 1+22B. 23C. 2+5D. 13

10. 甲、乙两辆摩托车同时从相距 20 km 的 A，B 两地出发，相向而行，图中 l1，l2 分别表示甲、乙两辆摩托车到 A 地的距离 Skm 与行驶时间 th 的函数关系．则下列说法错误的是
A. 乙摩托车的速度较快
B. 经过 0.3 小时甲摩托车行驶到 A，B 两地的中点
C. 当乙摩托车到达 A 地时，甲摩托车距离 A 地 503 km
D. 经过 0.25 小时两摩托车相遇

二、填空题（共6小题；共30分）
11. 若 ba=23，则 a+bb= ．

12. 将二次函数 y=x2−4x+7 化为 y=x−h2+k 的形式，结果为 y= ．

13. 若关于 x 的一元二次方程 x2+2k−1x+k2−1=0 有实数根，则 k 的取值范围是 ．

14. △ABC 的三边之比为 3:4:5，与其相似的 △DEF 的最短边是 9 cm，则其最长边的长是 ．

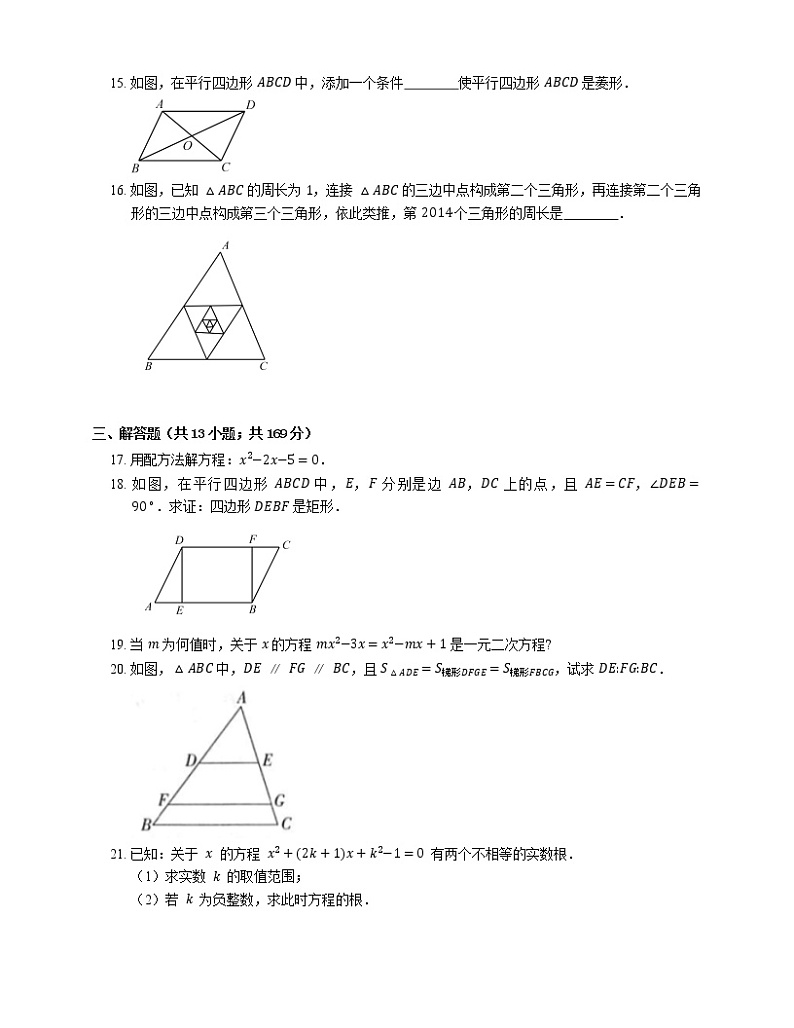
15. 如图，在平行四边形 ABCD 中，添加一个条件 使平行四边形 ABCD 是菱形．

16. 如图，已知 △ABC 的周长为 1，连接 △ABC 的三边中点构成第二个三角形，再连接第二个三角形的三边中点构成第三个三角形，依此类推，第 2014 个三角形的周长是 ．

三、解答题（共13小题；共169分）
17. 用配方法解方程：x2−2x−5=0．

18. 如图，在平行四边形 ABCD 中，E，F 分别是边 AB，DC 上的点，且 AE=CF，∠DEB=90∘．求证：四边形 DEBF 是矩形．

19. 当 m 为何值时，关于 x 的方程 mx2−3x=x2−mx+1 是一元二次方程?

20. 如图，△ABC 中，DE∥FG∥BC，且 S△ADE=S梯形DFGE=S梯形FBCG，试求 DE:FG:BC．

21. 已知：关于 x 的方程 x2+2k+1x+k2−1=0 有两个不相等的实数根．
（1）求实数 k 的取值范围；
（2）若 k 为负整数，求此时方程的根．

22. 如图，D 是 △ABC 的边 AC 上的一点，连接 BD．已知 ∠ABD=∠C，AB=6，AD=4．求线段 CD 的长．

23. 某旅游景区今年 9 月份游客人数比 8 月份增加了 22.5%，10 月份游客人数比 9 月份增加了 60%，求该旅游景区 9 月、 10 月游客人数的平均增长率．

24. 已知抛物线 y=−x2+bx+c 经过点 A3,0，B−1,0．
（1）求抛物线的解析式；
（2）求抛物线的顶点坐标．

25. 某校为更好地开展“传统文化进校园”活动，随机抽查了部分学生，了解他们最喜爱的传统文化项目类型（分为书法、围棋、戏剧、国画共 4 类），并将统计结果绘制成如图不完整的频数分布表及频数分布直方图．
最喜爱的传统文化项目类型频数分布表
项目类型频数频率书法类18a围棋类140.28喜剧类80.16国画类b0.20
根据以上信息完成下列问题：
（1）直接写出频数分布表中 a 的值；
（2）补全频数分布直方图；
（3）若全校共有学生 1500 名，估计该校最喜爱围棋的学生大约有多少人?

26. 阅读下面解题过程，解答相关问题．
请你利用上面求一元二次不等式解集的过程，求不等式 x2−3x≤0 的解集．
解：步骤一：构造二次函数 y= .在坐标系中画出示意图，如图.
步骤二：求得方程 的解为 .
步骤三：借助图象，可得不等式 x2−3x≤0 的解集为 .

27. 解方程：
（1）4x2−9=0；
（2）xx−2+x−2=0．

28. 如图，已知正方形 ABCD 的边长是 2，点 E 是 AB 边上一动点（点 E 与点 A，B 不重合），过点 E 作 FG⊥DE 交 BC 边于点 F 、交 DA 的延长线于点 G，且 FH∥AB．
（1）当 DE=433 时，求 AE 的长；
（2）求证：DE=GF；
（3）连接 DF，设 AE=x，△DFG 的面积为 y，求 y 与 x 之间的函数关系式．

29. 如图，在直角坐标系中有一直角三角形 AOB，O 为坐标原点，OA=1，tan∠BAO=3，将此三角形绕原点 O 逆时针旋转 90∘，得到 △DOC，抛物线 y=ax2+bx+c 经过点 A，B，C．
（1）求抛物线的解析式；
（2）若点 P 是第二象限内抛物线上的动点，其横坐标为 t，
①设抛物线对称轴 l 与 x 轴交于一点 E，连接 PE，交 CD 于 F，求出当 △CEF 与 △COD 相似时，点 P 的坐标；
②是否存在一点 P，使 △PCD 得面积最大?若存在，求出 △PCD 的面积的最大值；若不存在，请说明理由．
答案
第一部分
1. B
2. D
3. D
4. C【解析】∵x2+8x+7=0，
∴x2+8x+16=9，
∴x+42=9．
5. B
6. D
7. D【解析】抛物线 y=x+12−1 的顶点坐标为 −1,−1．
8. B【解析】如答图，延长 AB，BC，
∵AB∥CD，
∴∠ABC=∠5，∠ABC+∠4=180∘，
∴∠4+∠5=180∘．
根据多边形的外角和定理，得 ∠1+∠2+∠3+∠4+∠5=360∘，
∴∠1+∠2+∠3=360∘−180∘=180∘．
9. D【解析】作点 C 关于 AB 的对称点 F，连接 EF，交 AB 于点 P，作 EH⊥BC，交 BC 于点 H，
∵ 点 C，点 F 关于 AB 对称，点 P 在 AB 上，
∴ PF=PC，
∴ PE+PC=PE+PF，
∴ PE+PF 的最小值为 EF 的长，
∵ 四边形 ABCD 为正方形，点 E 是 AD 中点，
∴ EH=AB=2，BH=AE=1，
∴ FH=FB+BH=BC+BH=3，
∴ EF=EH2+FH2=13．
10. D
【解析】由图可得，
甲、乙行驶的路程相等，乙用的时间短，故乙的速度快，故选项A正确；
甲的速度为：20÷0.6=1003km/h，则甲行驶 0.3 h 时的路程为：1003×0.3=10km，即经过 0.3 小时甲摩托车行驶到 A，B 两地的中点，故选项B正确；
当乙摩托车到达 A 地时，甲摩托车距离 A 地：1003×0.5=503km，故选项C正确；
乙的速度为：20÷0.5=40km/h，则甲、乙相遇时所用的时间是 201003+40=311（小时），故选项D错误．
第二部分
11. 52
12. x−22+3
【解析】y=x2−4x+7=x2−4x+4+3=x−22+3．
13. k≤1
【解析】因为关于 x 的一元二次方程 x2+2k−1x+k2−1=0 有实数根，
所以 Δ=2k−12−4k2−1=−8k+8≥0，解得 k≤1．
14. 15 cm
15. AB=BC 或 AC⊥BD
【解析】当 AB=BC 或 AC⊥BD 时，四边形 ABCD 是菱形．
16. 122013
【解析】由三角形的中位线定理，第二个三角形的各边分别为 △ABC 各边的一半，∴ 第二个三角形的周长是 △ABC 周长的 12，即 1×12，第三个三角形的周长是第二个三角形周长的 12，即 1×12×12=122，第四个三角形的周长是第三个三角形周长的 12，即 1×12×12×12=123⋯⋯ 以此类推，第 2014 个三角形的周长是 122013．
第三部分
17. 移项，得
x2−2x=5.
配方，得
x2−2x+12=5+12,x−12=6.
由此可得
x−1=±6,x1=1+6,x2=1−6.
18. ∵ 四边形 ABCD 是平行四边形，
∴AB=CD，AB∥CD．
∵AE=CF，
∴BE=DF．
∴ 四边形 DEBF 是平行四边形．
又 ∵∠DEB=90∘，
∴ 四边形 DEBF 是矩形．
19. 方程变形为 m−1x2−3−mx−1=0．
∵ 关于 x 的方程 mx2−3x=x2−mx+1 是一元二次方程，
∴m−1≠0，
∴m≠1．
20. 因为 DE∥FG∥BC，
所以 △ADE∽△AFG∽△ABC，
因为 S△ADE=S梯形DFGE=S梯形FBCG，
所以 S△ADES△AFG=DEFG2=12，S△ADES△ABC=DEBC2=13，
所以 DE:FG:BC=1:2:3．
21. （1） 由题意，得 =2k+12−4k2−1=4k+5>0 ．解得 k>−54 ．
（2） ∵ k 为负整数，
∴ k=−1 ，
则方程为 x2−x=0 ，
解得 x1=0 ， x2=1 ．
22. 在 △ABD 与 △ACB 中，∠ABD=∠C，∠A=∠A，
∴△ABD∽△ACB．
∴ABAC=ADAB．
又 AB=6，AD=4，
∴6AC=46．
解得 AC=9．
∴CD=AC−AD=9−4=5．
23. 设该旅游景区 9 月、 10 月游客人数的平均增长率是 x．
依题意，得
1+x2=1+22.5%1+60%.
解得
x1=0.4=40%,x2=−2.4不合题意,舍去.
答：该旅游景区 9 月、 10 月游客人数的平均增长率是 40%．
24. （1） ∵ 抛物线 y=−x2+bx+c 经过点 A3,0，B−1,0，
∴ 抛物线的解析式为 y=−x−3x+1，
即 y=−x2+2x+3．
（2） ∵y=−x2+2x+3=−x−12+4，
∴ 抛物线的顶点坐标为 1,4．
25. （1） 14÷0.28=50（人），
a=18÷50=0.36．
（2） b=50×0.20=10，如图，
（3） 1500×0.28=420（人），
答：若全校共有学生 1500 名，估计该校最喜爱围棋的学生大约有 420 人．
26. 步骤一：x2−3x，
步骤二：x2−3x=0，x1=0，x2=3；
步骤三：0≤x≤3 .
27. （1） 分解因式得：
2x+32x−3=0.
解得：
x1=−32,x2=32.
（2） 分解因式得：
x+1x−2=0.
解得：
x1=−1,x2=2.
28. （1） ∵ 四边形 ABCD 是正方形，
∴∠DAE=90∘，
∵AD=2，DE=433，
∴AE=DE2−AD2=4332−22=233．
（2） ∵ 在正方形 ABCD 中，∠DAE=∠B=90∘，
∴ 四边形 ABFH 是矩形，
∴FH=AB=DA，
∵DE⊥FG，
∴∠G=90∘−∠ADE=∠DEA，
又 ∴∠DAE=∠FHG=90∘，
∴△FHG≌△DAEAAS，
∴DE=GF．
（3） ∵△FHG≌△DAE，
∴FG=DE=AD2+AE2=4+x2．
∵S△DGF=12FG⋅DE，
∴y=4+x22．
∴ 解析式为：y=4+x220