2021年北京平谷区山东庄中学八年级下期末数学试卷

这是一份2021年北京平谷区山东庄中学八年级下期末数学试卷

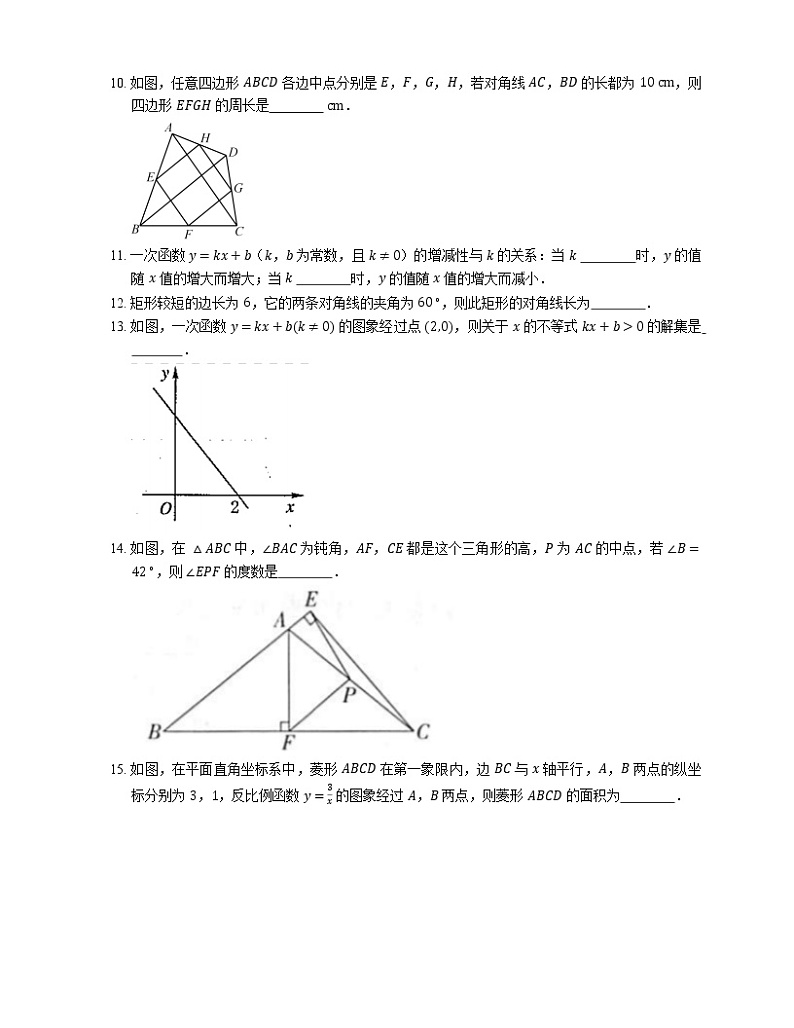
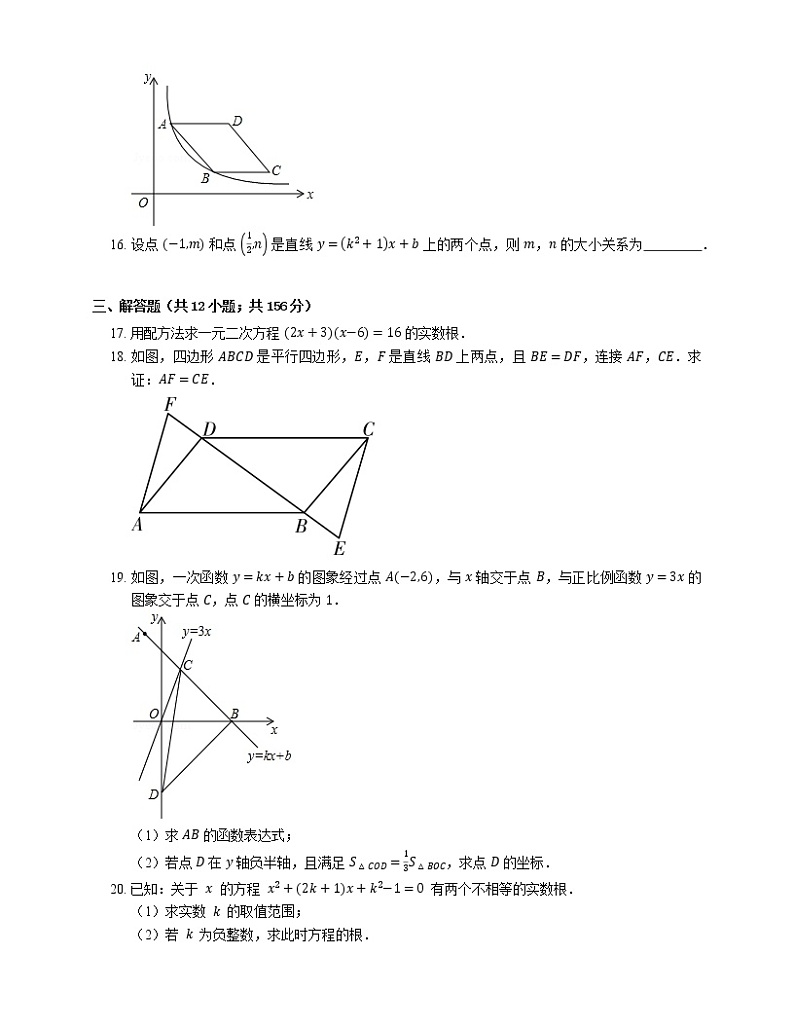
2021年北京平谷区山东庄中学八年级下期末数学试卷 一、选择题（共8小题；共40分）1. 如果点 P 的坐标是 3,1，那么点 P 在    A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 2. 下列四个图案中，是中心对称图形的为    A. B. C. D. 3. 六边形的内角和为    A. 1080∘ B. 720∘ C. 360∘ D. 180∘ 4. y=3x 与 y=3x−3 的图象在同一直角坐标系中的位置关系是    A. 相交 B. 互相垂直 C. 平行 D. 无法确定 5. 张阳把他和四位同学的年龄作为一组数据，计算出平均数是 15，方差是 0.5，则 10 年后张阳等 5 位同学的年龄的平均数和方差分别是    A. 25 和 10.5 B. 15 和 5 C. 25 和 0.5 D. 15 和 0.5 6. 某种植基地 2016 年蔬菜产量为 80 吨，预计 2018 年蔬菜产量达到 100 吨，求蔬菜产量的年平均增长率，设蔬菜产量的年平均增长率为 x，则可列方程为    A. 801+x2=100 B. 1001−x2=80 C. 801+2x=100 D. 801+x2=100 7. 下列说法不正确的是    A. 两组对边分别平行的四边形是平行四边形 B. 两组对边分别相等的四边形是平行四边形 C. 一组对边平行且相等的四边形是平行四边形 D. 一组对边平行、另一组对边相等的四边形是平行四边形 8. 已知 x=1 是一元二次方程 x2−2mx+1=0 的一个解，则 m 的值为    A. 0 或 −1 B. 0 或 1 C. 0 D. 1 二、填空题（共8小题；共40分）9. 一次函数 y=x+b 的图象经过 1,3，则 b=  ． 10. 如图，任意四边形 ABCD 各边中点分别是 E，F，G，H，若对角线 AC，BD 的长都为 10 cm，则四边形 EFGH 的周长是   cm． 11. 一次函数 y=kx+b（k，b 为常数，且 k≠0）的增减性与 k 的关系：当 k  时，y 的值随 x 值的增大而增大；当 k  时，y 的值随 x 值的增大而减小． 12. 矩形较短的边长为 6，它的两条对角线的夹角为 60∘，则此矩形的对角线长为  ． 13. 如图，一次函数 y=kx+bk≠0 的图象经过点 2,0，则关于 x 的不等式 kx+b>0 的解集是  ． 14. 如图，在 △ABC 中，∠BAC 为钝角，AF，CE 都是这个三角形的高，P 为 AC 的中点，若 ∠B=42∘，则 ∠EPF 的度数是  ． 15. 如图，在平面直角坐标系中，菱形 ABCD 在第一象限内，边 BC 与 x 轴平行，A，B 两点的纵坐标分别为 3，1，反比例函数 y=3x 的图象经过 A，B 两点，则菱形 ABCD 的面积为  ． 16. 设点 −1,m 和点 12,n 是直线 y=k2+1x+b 上的两个点，则 m，n 的大小关系为  ． 三、解答题（共12小题；共156分）17. 用配方法求一元二次方程 2x+3x−6=16 的实数根． 18. 如图，四边形 ABCD 是平行四边形，E，F 是直线 BD 上两点，且 BE=DF，连接 AF，CE．求证：AF=CE． 19. 如图，一次函数 y=kx+b 的图象经过点 A−2,6，与 x 轴交于点 B，与正比例函数 y=3x 的图象交于点 C，点 C 的横坐标为 1． （1）求 AB 的函数表达式；（2）若点 D 在 y 轴负半轴，且满足 S△COD=13S△BOC，求点 D 的坐标． 20. 已知：关于 x 的方程 x2+2k+1x+k2−1=0 有两个不相等的实数根．（1）求实数 k 的取值范围；（2）若 k 为负整数，求此时方程的根． 21. 某车间的甲、乙两名工人分别同时生产同种零件，在开始生产的前 2 个小时为生产磨合期，2 个小时后有一人停工一段时间对设备进行改良升级，以提升生产效率，另一人进入正常的生产模式．他们每人生产的零件总数 y（个）与生产时间 t（小时）的关系如图所示．根据图象回答： （1）在生产过程中，哪位工人对设备进行改良升级，停止生产多少小时?（2）当 t 为多少时，甲、乙所生产的零件个数第一次相等?甲、乙中，谁先完成一天的生产任务?（3）设备改良升级后每小时生产零件的个数是多少?与另一工人的正常生产速度相比每小时多生产几个? 22. 在平面直角坐标系中，四边形 ABCD 为矩形，A−1,m 和 Bn,2 关于 y 轴对称．（1）m=  ，n=  ；（2）矩形 ABCD 的中心在原点 O，直线 y=x+b 与矩形 ABCD 交于 P，Q 两点． ①当 b=0 时，线段 PQ 长度为  ； ②当线段 PQ 长度最大时，求 b 的取值范围． 23. 《淮南子?天文训》中记载了一种确定东西方向的方法，大意是：日出时，在地面上点 A 处立一根杆，在地面上沿着杆的影子的方向取一点 B，使 B，A 两点间的距离为 10 步（步是古代的一种长度单位），在点 B 处立一根杆；日落时，在地面上沿着点 B 处的杆的影子的方向取一点 C，使 C，B 两点间的距离为 10 步，在点 C 处立一根杆．取 CA 的中点 D，那么直线 DB 表示的方向为东西方向．（1）上述方法中，杆在地面上的影子所在直线及点 A，B，C 的位置如图所示，使用直尺和圆规，在图中作 CA 的中点 D（保留作图痕迹）； （2）在如图中，确定了直线 DB 表示的方向为东西方向，根据南北方向与东西方向互相垂直，可以判断直线 CA 表示的方向为南北方向，完成如下证明． 证明：在 △ABC 中，BA=  ，D 是 CA 的中点， 所以 CA⊥DB（  ）（填推理的依据）． ∵ 直线 DB 表示的方向为东西方向， ∴ 直线 CA 表示的方向为南北方向． 24. 如图，在 △ABC 中，M 是 AB 的中点，DM∥AC 交 BC 于 D，延长 DM 到 E，使 ME=DM，连接 AE，AD，BE． （1）四边形 ADBE 是平行四边形；（2）BD=CD． 25. 水利部确定每年的 3 月 22 日至 28 日为“中国水周”（1994 年以前为 7 月 1 日至 7 日），从 1991 年起，我国还将每年 5 月的第二周作为城市节约用水宣传周．某社区为了进一步提高居民珍惜水、保护水和水忧患意识，提倡节约用水，从本社区 5000 户家庭中随机抽取 100 户，调查他们家庭每月的平均用水量，并将调查的结果绘制成如下的两幅不完整的统计图表： 用户月用水量频数分布表 平均用水量吨频数频率3∼6吨100.16∼9吨m0.29∼12吨360.3612∼15吨25n15∼18吨90.09 请根据上面的统计图表，解答下列问题：（1）在频数分布表中：m=  ，n=  ．（2）根据题中数据补全频数直方图；（3）如果自来水公司将基本月用水量定为每户每月 12 吨，不超过基本月用水量的部分享受基本价格，超出基本月用水量的部分实行加价收费，那么该社区用户中约有多少户家庭能够全部享受基本价格? 26. 如图，直线 y=−x+4 与 x 轴交于点 A，与 y 轴交于点 B，点 C 在直线 AB 上，且 AC=2BC，求点 C 的坐标． 27. 将一副三角板按如图所示的方式摆放，AD 是等腰直角三角板 ABC 斜边 BC 上的高，另一块三角板 DMN 的直角顶点与点 D 重合，DM，DN 分别交 AB，AC 于点 E，F．请判断 △DEF 的形状，并证明你的结论． 28. （1）同学们都知道，∣5−−2∣ 表示 5 与 −2 之差的绝对值，实际上也可理解为 5 与 −2 两数在数轴上所对的两点之间的距离．试探索： 1 求 ∣5−−2∣=  ． 2 找出所有符合条件的整数 x，使得 ∣x+5∣+∣x−2∣=7 这样的整数是  ． 3 由以上探索猜想对于任何有理数 x，∣x−3∣+∣x−6∣ 是否有最小值?如果有写出最小值如果没有说明理由．（2）若 a 、 b 、 c 均为整数，且 ∣a−b∣3+∣c−a∣2=1，求 ∣a−c∣+∣c−b∣+∣b−a∣ 的值.答案第一部分1. A 2. D 3. B 4. C 5. C 【解析】设张阳及其他四名同学的年龄分别为 x1，x2，x3，x4，x5，平均年龄为 x=15，方差 s12=15x1−x2+x2−x2+x3−x2+x4−x2+x5−x2，十年后五名同学的年龄分别为 x1+10，x2+10，x3+10，x4+10，x5+10，平均年龄为 x+10=25，方差 s22=15x1+10−x−102+x2+10−x−102+x3+10−x−102+x4+10−x−102+x5+10−x−102=15x1−x2+x2−x2+x3−x2+x4−x2+x5−x2=s12=0.5.6. A 7. D 8. D 第二部分9. 210. 20【解析】∵E，F，G，H 是四边形 ABCD 各边中点， ∴HG=12AC，EF=12AC，GF=HE=12BD， ∴ 四边形 EFGH 的周长是 HG+EF+GF+HE=12AC+AC+BD+BD=12×10+10+10+10=20cm.11. >0，<012. 1213. x<2【解析】由图象可得：当 x<2 时，kx+b>0，所以关于 x 的不等式 kx+b>0 的解集是 x<2．14. 96∘【解析】∵CE⊥BA，∠B=42∘， ∴∠BCE=48∘， ∵AF⊥BC，CE⊥BA，P 为 AC 的中点， ∴PF=12AC=PC，PE=12AC=PC， ∴∠PFC=∠PCF，∠PEC=∠PCE， ∴∠EPF=2∠PCF+2∠PCE=2∠BCE=96∘．故答案为 96∘．15. 42【解析】过点 A 作 x 轴的垂线，与 CB 的延长线交于点 E， ∵A，B 两点在反比例函数 y=3x 的图象上且纵坐标分别为 3，1， ∴A，B 横坐标分别为 1，3， ∴AE=2，BE=2， ∴AB=22， S菱形ABCD=底×高=22×2=42．16. m0 ．解得 k>−54 ．      （2） ∵ k 为负整数， ∴ k=−1 ，则方程为 x2−x=0 ，解得 x1=0 ， x2=1 ．21. （1） 由图象可知：在生产的过程中，甲进行了改良，停止生产时间：5−2=3 小时．      （2） 由图象可知，当 t=3 时，甲和乙第一次生产零件的个数相同；甲、乙中，甲先完成一天的生产任务．      （3） 设备改良升级后，甲每小时生产零件的个数是：40−10÷7−5=15 个；乙每小时生产零件的个数是：40−4÷8−2=6 个；因此，改良后，甲每小时比乙多生产：15−6=9 个．22. （1） 2；1【解析】∵A−1,m 和 Bn,2 关于 y 轴对称， ∴n=1，m=2；故答案为 2，1．      （2） ① 22 ②当直线 y=x+b 过点 D 和 B 时，PQ 一样大，并且是最大，此时是 PQ 最大的分界点，如图所示： ∴ 当直线 y=x+b 过点 D−1,−2 时，则有 −2=−1+b， ∴b=−1；当直线 y=x+b 过点 B1,2 时，则有 2=1+b， ∴b=1； ∴ 当线段 PQ 长度最大时，b 的取值范围为 −1≤b≤1．【解析】① ∵ 矩形 ABCD 的中心在原点 O， ∴ 点 C，D 分别是点 A，B 关于原点的对称点， ∴C1,−2，D−1,−2， ∵ 四边形 ABCD 是矩形， ∴AD∥BC∥y 轴， ∴ 直线 AD 为 x=−1，直线 BC 为 x=1，当 b=0 时，则有 y=x， ∵ 假设直线 y=x 与 AD，BC 交于 P，Q 两点， ∴P−1,−1，Q1,1， ∴ 根据两点距离公式可得 PQ=1+12+1+12=22；故答案为 22．23. （1） 如图，点 D 即为所求．      （2） BC；三线合一24. （1） ∵M 是 AB 的中点， ∴AM=BM．又 ∵ME=DM， ∴ 四边形 ADBE 是平行四边形．      （2） 在平行四边形 ADBE 中，AE=BD，AE∥BD， ∵AE∥DC，DE∥AC， ∴ 四边形 AEDC 是平行四边形， ∴AE=DC， ∴BD=CD．25. （1） 20；0.25【解析】m=100×0.2=20，n=25÷100=0.25．      （2） 补全频数直方图如图：      （3） 5000÷100=50， 10+20+36×50=3300（户）．故该社区用户中约有 3300 户家庭能够全都享受基本价格．26. 易求 A4,0，B0,4， ∵AC=2BC， ∴S△AOC=2S△BOC，①点 C 在线段 AB 上时， S△AOC=23S△AOB=163， ∴12⋅4⋅yC=163， ∴yC=83，把 yC=83 代入 y=−x+4 得 xC=43， ∴C43,83；②点 C 在线段 AB 的延长线上时， S△AOC=2S△AOB=16， ∴yC=8， ∴xC=−4， ∴C−4,8，综上，C43,83或−4,8．27. △DEF 是等腰直角三角形．证明如下： ∵△ABC 是等腰直角三角形，AD⊥BC， ∴∠DAE=∠DAC=∠C=45∘，∠ADC=90∘． ∴AD=CD． ∵∠MDN=90∘， ∴∠ADF+∠ADE=90∘． ∵∠CDF+∠ADF=∠ADC=90∘， ∴∠ADE=∠CDF．在 △ADE 和 △CDF 中，∠DAE=∠C,AD=CD,∠ADE=∠CDF, ∴△ADE≌△CDFASA． ∴DE=DF．又 ∠MDN=90∘，即 ∠EDF=90∘， ∴△DEF 是等腰直角三角形．28. （1） 17． 2 画出数轴如下，通过观察：−5 到 2 之间的数都满足 ∣x+5∣+∣x−2∣=7，这样的整数有 −5，−4，−3，−2，−1，0，1，2． 3 猜想对于任何有理数 x，∣x−3∣+∣x−6∣ 有最小值 =3．因为当 x 在 3 到 6 之间时，x 到 3 的距离与 x 到 6 的距离的和是 3，并且是最小的．当 x<3 和 x>6 时，x 到 3 的距离与 x 到 6 的距离的和都 >3．      （2） ∵∣a−b∣3+∣c−a∣2=1，并且 a 、 b 、 c 均为整数 ∴∣a−b∣ 和 ∣c−a∣=0 或 1 ∴ 当 ∣a−b∣=1 时，∣c−a∣=0，则 c=a，∣c−b∣=1． ∴∣a−c∣+∣c−b∣+∣b−a∣=0+1+1=2．当 ∣a−b∣=0 时，∣c−a∣=1，则 b=a，∣c−b∣=1． ∴∣a−c∣+∣c−b∣+∣b−a∣=1+1+0=2 .综上可知：∣a−c∣+∣c−b∣+∣b−a∣=2 .