2021年北京朝阳区东北师大朝阳学校（初中部）八年级上期末数学试卷

这是一份2021年北京朝阳区东北师大朝阳学校（初中部）八年级上期末数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 已知一个数的算术平方根是 7，则这个数是
A. 7B. ±7C. 49D. ±49

2. 下列是必然事件的是
A. 买一张福利彩票，一定能中奖
B. 掷一枚硬币，一定是国徽朝上
C. 只要投篮，一定能投中得 2 分
D. 常态下温度达到零下 10 度，水一定结冰

3. 如果把分式 2xx+y 中的 x 和 y 时扩大 3 倍，则分式的值
A. 扩大 3 倍B. 扩大 9 倍C. 缩小 9 倍D. 不变

4. 下列图形中对称轴的条数最少的是
A. 正五边形B. 等边三角形
C. 正方形D. 长宽不等的长方形

5. 使代数式 1x+3+4−3x 有意义的整数 x 有
A. 5 个B. 4 个C. 3 个D. 2 个

6. 如图所示， △ABC 中 AB 边上的高线是
A. 线段 DAB. 线段 CAC. 线段 CDD. 线段 BD

7. 在数轴上，点 A 到原点的距离为 2−1，那么点 A 表示的数是
A. 2−1B. 1−2
C. 2−1 或 1−2D. 以上答案都错误

8. 甲、乙两人各用一张正方形的纸片 ABCD 折出一个 45∘ 角（如图），两人做法如下：
甲：将纸片沿对角线 AC 折叠，使 B 点落在 D 点上，则 ∠1=45∘；
乙：将纸片沿 AM，AN 折叠，分别使 B，D 落在对角线 AC 上的一点 P，则 ∠MAN=45∘．
对于两人的做法，下列判断正确的是
A. 甲乙都对B. 甲对乙错C. 甲错乙对D. 甲乙都错

二、填空题（共8小题；共40分）
9. 一口袋内装有编号分别为 1，2，3，4，5，6，7 的七个球（除编号外都相同），从中随机摸出一个球，则摸出编号为偶数的球的概率是 ．

10. 计算：xy2xy= ．

11. 介于 −3∼5 的整数有 ．

12. 在 △ABC 中，D 为边 BC 的中点，如果 AB=6，AC=8，那么线段 BD 的长的取值范围是 ．

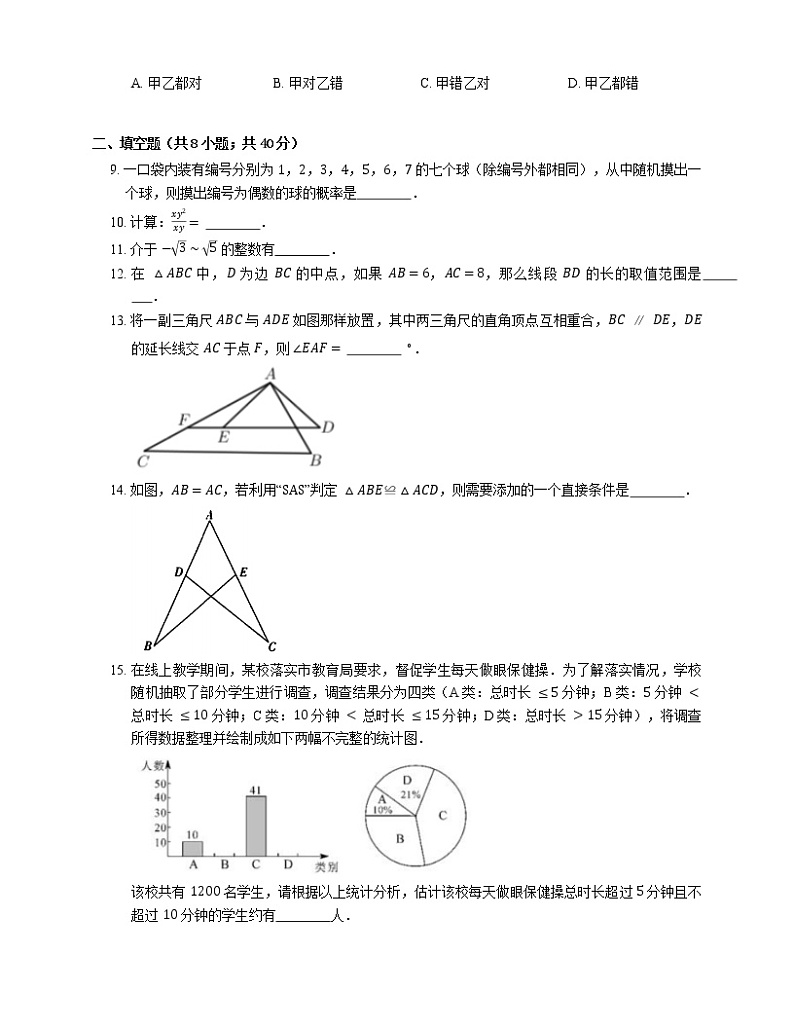
13. 将一副三角尺 ABC 与 ADE 如图那样放置，其中两三角尺的直角顶点互相重合，BC∥DE，DE 的延长线交 AC 于点 F，则 ∠EAF= ∘．

14. 如图，AB=AC，若利用“SAS”判定 △ABE≌△ACD，则需要添加的一个直接条件是 ．

15. 在线上教学期间，某校落实市教育局要求，督促学生每天做眼保健操．为了解落实情况，学校随机抽取了部分学生进行调查，调查结果分为四类（A类：总时长 ≤5 分钟；B类：5 分钟 < 总时长 ≤10 分钟；C类：10 分钟 < 总时长 ≤15 分钟；D类：总时长 >15 分钟），将调查所得数据整理并绘制成如下两幅不完整的统计图．
该校共有 1200 名学生，请根据以上统计分析，估计该校每天做眼保健操总时长超过 5 分钟且不超过 10 分钟的学生约有 人．

16. 如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”（如图中的实线）．其实他们仅仅少走了 m，却踩伤了花草．

三、解答题（共12小题；共156分）
17. 计算：9+3−27−−22+1−3．

18. 15×2−315÷5

19. 解方程：2−xx−3=1−13−x．

20. 已知，如图，△ABC 和 △BDE 都是等边三角形，且点 D 在 AC 上．
（1）求证：AE∥BC；
（2）直接写出 AE，AD 和 AB 之间的关系；

21. 如图 1，有一块直角三角形的绿地，量得两直角边长分别为 20 m，15 m，现要将绿地扩充成等腰三角形，且扩充部分是以 20 m 为直角边的直角三角形，求扩充后等腰三角形绿地的周长．

22. 化简：2aa+1−2a−4a2−1÷a−2a2−2a+1．

23. 某工厂计划加工生产 800 件产品，当完成 200 件产品后，改进了技术，提高了效率，改进后每小时生产的产品数是原来的 1.2 倍，因此提前了 25 小时完工．求原来每小时加工生产的产品数．

24. 小手拉大手，共创文明城．某校为了了解家长对南宁市创建全国文明城市相关知识的知晓情况，通过发放问卷进行测评，从中随机抽取 20 份答卷，并统计成绩（成绩得分用 x 表示，单位：分），收集数据如下：
90829986989690100898387888190931001009692100
整理数据：
80≤x<8585≤x<9090≤x<9595≤x<10034a8
分析数据：
平均分中位数众数92bc
根据以上信息，解答下列问题：
（1）直接写出上述表格中 a，b，c 的值；
（2）该校有 1600 名家长参加了此次问卷测评活动，请估计成绩不低于 90 分的人数是多少?
（3）请从中位数和众数中选择一个量，结合本题解释它的意义．

25. 如图，在 △ABC 中，AB=AC，AD 是 BC 边上的中线，BE⊥AC 于点 E．求证：∠CBE=∠BAD．

26. 解答下列各题：
（1）求不等式 2x+13≤3x−25+1 的非负整数解；
（2）解方程：1−xx−2=5xx2−4．

27. 已知：点 O 为 △ABC 的边 AC 的中点，点 P 为射线 OA 上的一个动点（点 P 不与点 A 重合），分别过点 A，C 向直线 BP 作垂线，垂足分别为 E，F．
（1）当点 P 与点 O 重合时，如图 1，求证：OE=OF．
（2）直线 BP 绕点 B 逆时针方向旋转，当 ∠OFE=30∘ 时．
①当点 P 在线段 OA 上，如图 2，猜想线段 CF，AE，OE 之间有怎样的数量关系?请写出你的猜想，并给予证明．
②当点 P 在线段 OA 的延长线上，如图 3，线段 CF，AE，OE 之间又有怎样的数量关系，请写出你的结论，并说明理由．（温馨提示：直角三角形斜边上的中线等于斜边的一半）

28. 如图，已知等腰 △ABC 的底边 BC=13，D 是腰 AB 上一点，且 CD=12，BD=5．
（1）求证：△BDC 是直角三角形；
（2）求 AC 的长．
答案
第一部分
1. C
2. D
3. D【解析】x，y 都扩大 3 倍，故 原式=2×3x3x+3y=6x3x+y=2xx+y，故分式的值不变．
4. D
5. B
【解析】根据题意，代数式要有意义，必须满足 x+3>0 且 4−3x≥0，即 −36. C
7. C
8. A
第二部分
9. 37
【解析】编号为偶数的球有：2，4，6 一共 3 个，总共有 7 个球，
所以 P=37．
10. y
【解析】xy2xy=xy⋅yxy=y．
11. −1，0，1，2
12. 113. 15
【解析】∵BC∥DE，
∴∠C=∠AFD=30∘，
又 ∵∠AED=45∘，
∴∠FAE=45∘−30∘=15∘．
14. AE=AD
【解析】需要添加的一个直接条件是 AE=AD，
理由：在 △ABE 和 △ACD 中，
AB=AC,∠A=∠A,AE=AD,
∴△ABE≌△ACDSAS．
15. 336
16. 4
第三部分
17. 原式=3−3−2+3−1=3−3.
18. 6−33
19. 方程两边乘 x−3，得
2−x=x−3+1.
解得
x=2.
经检验，x=2 是原分式方程的解．
20. （1） ∵△ABC 和 △BDE 都是等边三角形，
∴AB=BC，BE=BD，∠ABC=∠DBE=∠C=60∘，
∴∠ABC−∠ABD=∠DBE−∠ABD，
∴∠DBC=∠EBA，
∴△DBC≌△EBASAS，
∴∠C=∠EAB=∠ABC，
∴EA∥BC．
（2） AE+AD=AB．
【解析】∵△DBC≌△EBA，
∴AE=CD，
∵AD+CD=AC=AB，
∴AE+AD=AB．
21. ①如图 1，当 AD=AB 时，DC=BC=15，AD=25，
∴ 周长为 80 m．
②如图 2，
当 AB=DB 时，AB=25=DB，CD=10，AD=105，
∴ 周长为 50+105m．
③如图 3，
当 AD=DB 时，设 DC=x，
则 AD=x+15，
∴ x+152=x2+202，x=356，
∴ 周长为 2003 m．
22. 原式=2aa+1−2a−2a+1a−1⋅a−12a−2=2aa+1−2a−1a+1=2a+1.
23. 设原来每小时加工生产的产品数为 x 件．
根据题意，得
800x−200x+6001.2x=25.
整理，得
24x−241.2x=1.
解得
x=4.
经检验：x=4 是原方程的解且符合题意．
答：原来每小时加工生产的产品数为 4 件．
24. （1） a=5，b=90+922=91，c=100
【解析】将这组数据重新排列为：
81828386878889909090929396969899100100100100∴a=5
，b=90+922=91，c=100；
（2） 估计成绩不低于 90 分的人数是 1600×1320=1040（人）．
（3） 中位数，
在被调查的 20 名学生中，中位数为 91 分，有一半的人分数都是在 91 分以上．
25. ∵AB=AC，AD 是 BC 边上的中线，
∴AD⊥BC，∠BAD=∠CAD，
∵BE⊥AC，
∴∠BEC=∠ADC=90∘，
∴∠CBE=90∘−∠C，∠CAD=90∘−∠C，
∴∠CBE=∠CAD，
∴∠CBE=∠BAD．
26. （1） 去分母得：
10x+5≤9x−6+15,
移项合并得：
x≤4,
则不等式的非负整数解为 0，1，2，3，4；
（2） 去分母得：
x2−4−x2−2x=5x,
解得：
x=−47,
经检验 x=−47 是分式方程的解．
27. （1） ∵AE⊥PB，CF⊥BP，
∴∠AEO=CFO=90∘，
在 △AEO 和 △CFO 中，
∠AEO=∠CFO,∠AOE=∠COF,AO=OC,
∴∠AOE≌△COFAAS，
∴OE=OF．
（2） ①延长 EO 交 CF 于点 G，
∵AE⊥BP，CF⊥BP，
∴AE∥CF，
∴∠EAO=∠GCO，
在 △EOA 和 △GOC 中，
∠EAO=∠GCO,AO=OC,∠AOE=∠COG,
∴△EOA≌△GOCASA，
∴EO=GO，
AE=CG，
在 Rt△EFG 中，
∵EO=OG，
∴OE=OF=GO，
∵∠OFE=30∘，
∴∠OFG=90∘−30∘=60∘，
∴△OFG 是等边三角形，
∴OF=GF，
∵OE=OF，
∴OE=FG，
∵CF=FG+CG，
∴CF=OE+AE．
②延长 EO 交 FC 的延长线于点 G，
∵AE⊥BP，CF⊥BP，
∴AE∥CF，
∴∠AEO=∠G，
∴ 在 △AOE 和 △COG 中，
∠AEO=∠G,∠AOE=∠GOC,AO=OC,
∴△AOE≌△COGAAS，
∴OE=OG，AE=CG，
在 Rt△EFG 中，
∵OE=OG，
∴OE=OF=OG，
∵∠OFE=30∘，
∴∠OFG=90∘−30∘=60∘，
∴△OFG 是等边三角形，
∴OF=FG，
∵OE=OF，
∴OE=FG，
∵CF=FG−CG，
∴CF=OE−AE．
28. （1） ∵BC=13，CD=12，BD=5，
∴BC2=BD2+CD2，
∴△BDC 为直角三角形．
（2） 设 AB 的长为 x，
∵△ABC 是等腰三角形，
∴AB=AC=x．
∵AC2=AD2+CD2，
∴x2=x−52+122．
解得 x=16.9，
∴AC=16.9．