2021年北京石景山区北京市九中八年级上期末数学试卷

这是一份2021年北京石景山区北京市九中八年级上期末数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 2017 年 12 月某种流感病毒肆虐，该种病毒的直径在 0.00000012 米左右，该数用科学记数法表示应为
A. 0.12×10−6B. 12×10−8C. 1.2×10−6D. 1.2×10−7

2. 如图，△ABC≌△DCB，若 AC=7，BE=5，则 DE 的长为
A. 2B. 3C. 4D. 5

3. 分式 −11−x 可变形为
A. 1x+1B. −1x+1C. 1x−1D. −1x−1

4. 已知一次函数 y=kx+b，y 随 x 的增大而减小，则该函数的图象一定经过
A. 第一、二、三象限B. 第一、二、四象限
C. 第一、三、四象限D. 第二、三、四象限

5. 2017 年 6 月北京国际设计周面向社会公开征集“二十四节气”标识系统设计，以期通过现代设计的手段，尝试推动我国非物质文化遗产创新传承与发展．下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”，其中是轴对称图形的是
A. B.
C. D.

6. 二次根式 −102 的值是
A. 10B. −10C. −10 或 10D. 100

7. 小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．
如图：一把直尺压住射线 OB，另一把直尺压住射线 OA 并且与第一把直尺交于点 P，小明说：“射线 OP 就是 ∠BOA 的角平分线．”他这样做的依据是
A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确

8. 已知在 △ABC 中，AB=AC，AD⊥BC，垂足为点 D，那么下列结论不一定成立的是
A. AD=BDB. BD=CD
C. ∠BAD=∠CADD. ∠B=∠C

二、填空题（共8小题；共40分）
9. 如图，在 △ABC 中，AB=AD=DC，∠BAD=20∘，则 ∠C= ．

10. 如图，BC=EF，∠1=∠F．请你添加一个适当的条件 ，使得 △ABC≌△DEF（只需填一个答案即可）．

11. 若函数的图象经过点 A1,2，点 B2,1，写出一个符合条件的函数表达式 ．

12. 如图，Rt△ACB 中，∠ACB=90∘，∠A=15∘，AB 的垂直平分线与 AC 交于点 D，与 AB 交于点 E，连接 BD．若 AD=14，则 BC 的长为 ．

13. 如图，直线 y=x+b 与直线 y=kx+6 交于点 P3,5，则关于 x 的不等式 kx+6>x+b 的解集是 ．

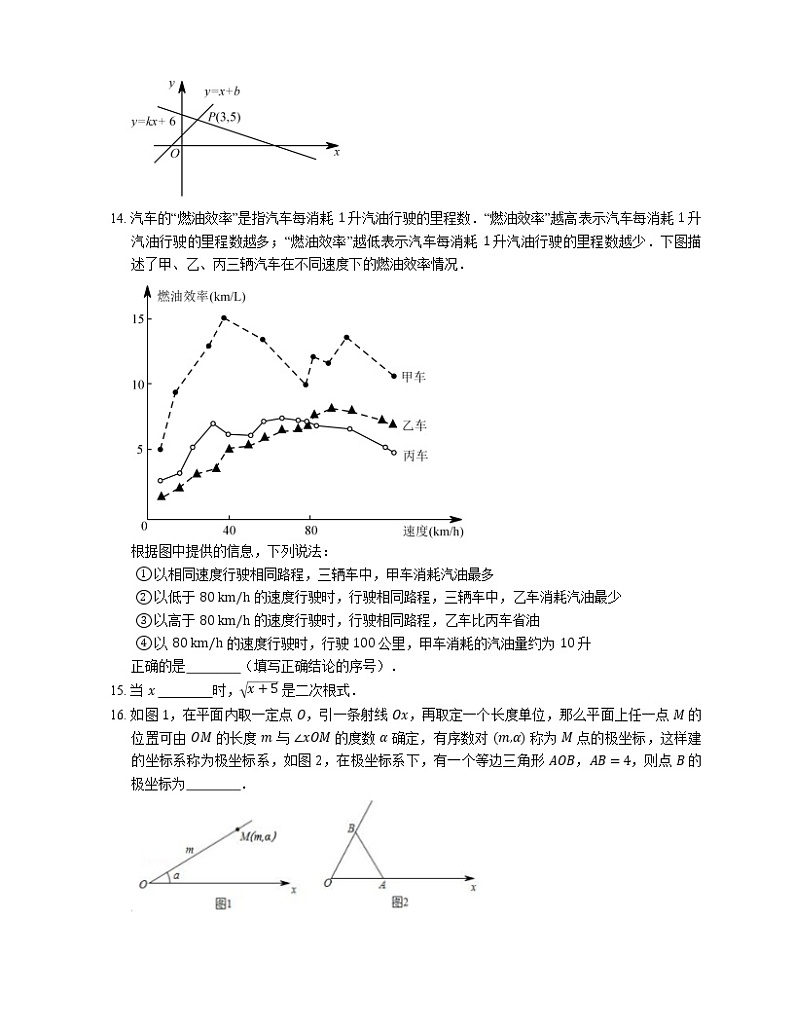
14. 汽车的“燃油效率”是指汽车每消耗 1 升汽油行驶的里程数．“燃油效率”越高表示汽车每消耗 1 升汽油行驶的里程数越多；“燃油效率”越低表示汽车每消耗 1 升汽油行驶的里程数越少．下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况．
根据图中提供的信息，下列说法：
① 以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多
② 以低于 80 km/h 的速度行驶时，行驶相同路程，三辆车中，乙车消耗汽油最少
③ 以高于 80 km/h 的速度行驶时，行驶相同路程，乙车比丙车省油
④ 以 80 km/h 的速度行驶时，行驶 100 公里，甲车消耗的汽油量约为 10 升
正确的是 （填写正确结论的序号）．

15. 当 x 时，x+5 是二次根式．

16. 如图 1，在平面内取一定点 O，引一条射线 Ox，再取定一个长度单位，那么平面上任一点 M 的位置可由 OM 的长度 m 与 ∠xOM 的度数 α 确定，有序数对 m,α 称为 M 点的极坐标，这样建的坐标系称为极坐标系，如图 2，在极坐标系下，有一个等边三角形 AOB，AB=4，则点 B 的极坐标为 ．

三、解答题（共12小题；共156分）
17. 解方程：3x+2=2xx−1．

18. 某地区要在区域 S 内（即 ∠COD 内部）建一个超市 M，如图，按照要求，超市 M 到两个新建的居民小区 A，B 的距离相等，到两条公路 OC，OD 的距离也相等．这个超市应该建在何处?（要求：尺规作图，不写作法，保留作图痕迹）

19. 2017 年 5 月，“一带一路”国际合作高峰论坛在中国北京成功召开．会议期间为方便市民出行，某路公交车每天比原来的运行增加 30 车次．经调研得知，原来这路公交车平均每天共运送乘客 5600 人，高峰论坛期间这路公交车平均每天共运送乘客 8000 人，且平均每车次运送乘客与原来的数量基本相同，问高峰论坛期间这路公交车每天运行多少车次?

20. 画出函数 y=x−1 的图象．
（1）函数 y=x−1 的自变量 x 的取值范围是 ．
（2）列表（把表格补充完整）．
x⋯⋯−2−101234⋯⋯y
（3）描点、连线．
（4）结合图象，写出函数的一条性质 ．

21. 已知：如图，△ABC 中，AB=AC，∠ABC=60∘，AD=CE，求 ∠BPD 的度数．

22. 已知一次函数 y=−x+4 的图象与 x 轴、 y 轴的交点分别为 A，B，点 P 在直线 y=2x 上．
（1）若点 P 是一次函数 y=−x+4 的图象与直线 y=2x 的交点，求 △OBP 的面积；
（2）若点 P 的坐标为 3,6，求 △ABP 的面积；
（3）若 △ABP 的面积为 12 时，求点 P 的坐标．

23. 已知：∠MON=α，点 P 是 ∠MON 平分线上一点，点 A 在射线 OM 上，作 ∠APB=180∘−α，交直线 ON 于点 B，PC⊥ON 于 C．
（1）如图 1，若 ∠MON=90∘ 时，求证：PA=PB；
（2）如图 2，若 ∠MON=60∘ 时，写出线段 OB，OA 及 BC 之间的数量关系，并说明理由；
（3）如图 3，若 ∠MON=60∘ 时，点 B 在射线 ON 的反向延长线上时，（2）中结论还成立吗?若不成立，直接写出线段 OB，OA 及 BC 之间的数量关系（不需要证明）．

24. 已知 A2,0，B2,4，定义：若平面内点 P 关于直线 AB 的对称点 Q 在图形 M 内或图形的边界上，则称点 P 是图形 M 关于直线 AB 的“反称点”．
（1）已知 C5,0，D5,3．
① 点 M10,3，M2−0.5,2，M3−2,1，则是 △ACD 关于直线 AB 的“反称点”的是 ；
② 若直线 y=2x+m 上存在 △ACD 关于直线 AB 的“反称点”，求 m 的取值范围；
（2）已知点 E1,0，F5,0，G3,23，点 Px,y 在直线 y=x+1 上，且点 P 是 △EFG 的反称点，求点 P 横坐标的取值范围．

25. 把下列各式分解因式：
（1）2a2−12ab+18b2；
（2）x2−2y2−1−2y2．

26. 如图，点 D，A，C 在同一直线上，AB∥CE，AB=CD，∠B=∠D，求证：BC=DE．

27. 计算：12−418−3−8．

28. 先化简： a2−b2a2−ab÷a+2ab+b2a ，当 b=−1 时，再从 −2答案
第一部分
1. D【解析】0.00000012=1.2×10−7．
2. A【解析】∵△ABC≌△DCB，
∴BD=AC=7，
∵BE=5，
∴DE=BD−BE=2．
3. C【解析】因为 −11−x=−1−x−1=1x−1，
所以C正确．
4. B【解析】对于一次函数 y=kx+b，当 k>0，b>0 时，函数经过一、二、三象限；
当 k>0，b<0 时，函数经过一、三、四象限；
当 k<0，b>0 时，函数经过一、二、四象限；
当 k<0，b<0 时，函数经过二、三、四象限．
所以函数图象一定经过第一、二、四象限．
5. D
6. A
7. A【解析】如图所示：过两把直尺的交点 P 作 PE⊥AO，PF⊥BO，
∵ 两把完全相同的长方形直尺，
∴PE=PF，
∴OP 平分 ∠AOB（角的内部到角的两边的距离相等的点在这个角的平分线上），
故选：A．
8. A
第二部分
9. 40∘
【解析】∵AB=AD，∠BAD=20∘，
∴∠B=12180∘−∠BAD=12180∘−20∘=80∘．
∵∠ADC 是 △ABD 的外角，
∴∠ADC=∠B+∠BAD=80∘+20∘=100∘．
∵AD=DC．
∴∠C=12180∘−∠ADC=12180∘−100∘=40∘．
10. AC=DF（答案不唯一）
【解析】添加条件 AC=DF 可使得 △ABC≌△DEF．
理由如下：
在 △ABC 与 △DEF 中，
BC=EF,∠1=∠F,AC=DF,
∴△ABC≌△DEFSAS．
11. y=−x+3
【解析】设 y=kx+b，则：k+b=2,2k+b=1, 解得：k=−1,b=3,
∴ 符合条件的函数表达式为 y=−x+3．
12. 7
【解析】∵DE 是 AB 的垂直平分线，
∴AD=BD=14，
∴∠A=∠ABD=15∘，
∴∠BDC=∠A+∠ABD=15∘+15∘=30∘．
在 Rt△BCD 中，
BC=12BD=12×14=7．
13. x<3
【解析】当 x<3 时，x+b14. ③④
【解析】① 以相同速度行驶相同路程，三辆车中，甲车燃油效率最高，甲车消耗汽油最少，故 ① 错误；
② 以低于 80 km/h 的速度行驶时，行驶相同路程，三辆车中，甲车燃油效率最高，甲车消耗汽油最少，故 ② 错误；
③ 以高于 80 km/h 的速度行驶时，行驶相同路程，乙车燃油效率大于丙车燃油效率，乙车比丙车省油，故 ③ 正确；
④ 由图象可知当速度为 80 km/h 时，甲车的燃油效率为 10 km/L，即甲车行驶 10 km 时，耗油 1 L，行驶 100 km 时耗油 10 L，故 ④ 正确；
15. ≥−5
16. 4,60∘
第三部分
17. 方程两边同时乘以 xx−1 得：
3x−1+2xx−1=2x2.
去括号得：
3x−3+2x2−2x=2x2.
整理得：
x=3.
经检验：x=3 是原方程的根．
18. 如图所示，点 M 就是所要求作的建立超市的位置．
19. 设高峰论坛期间这路公交车每天运行 x 车次，则原来每天运行 x−30 车次．由题意得：
5600x−30=8000x.
解得：
x=100.
经检验，x=100 是原分式方程的解，且符合题意．
答：高峰论坛期间这路公交车每天运行 100 车次．
20. （1） 任意实数
（2） 见下表．
x⋯⋯−2−101234⋯⋯y3210123
（3） 如图．
（4） ①函数的最小值为 0（或当 x=1 时，函数取得最小值，且最小值为 0）．
②当 x<1 时，y 随 x 的增大而减小或当 x>1 时，y 随 x 的增大而增大．
③函数图象关于直线 x=1 对称（答案不唯一）
21. ∵AB=AC，∠ABC=60∘，
∴△ABC 是等边三角形，
∴AC=BC，∠A=∠ACB=60∘．
在 △ACD 和 △BCE 中，
AD=CE,∠A=∠ACB,AC=BC,
∴△ACD≌△CEBSAS，
∴∠ACD=∠CBE，
∴∠BPD=∠CBE+∠BCD=∠ACD+∠BCD=∠ACB=60∘．
22. （1） 依题意，得：A4,0，B0,4．
由 y=−x+4,y=2x, 解得 x=43，y=83，
∴P43,83．
∴S△OBP=12×OB×xp=12×4×43=83．
（2） ∵S△OAB+S△ABP=S△OAP+S△OBP，
∴12×OA×OB+S△ABP=12×OA×yp+12×OB×xp，
∵P3,6，
∴S△ABP=10．
（3） 设 Px,2x，
若点 P 在第一象限时，由（2）可知，x=103，
∴P103,203；
若点 P 在第三象限时，
∵S△ABP=S△OAP+S△OBP+S△OAB，
∴P23,43，
∴P 点坐标为：103,203 或 23,43．
23. （1） 作 PD⊥OM 于点 D，如图 1，
∵ 点 P 在 ∠MON 的平分线上，且 PC⊥ON 于 C，
∴PC=PD．
∵∠MON=90∘，
∴∠APB=90∘，∠CPD=90∘，
∴∠APD=∠BPC．
又 ∵∠PDA=∠PCB=90∘，
∴△APD≌△BPCASA，
∴AP=BP．
（2） 结论：OA=OB+2BC．
理由如下：
作 PD⊥OM 于点 D，如图 2，
同（1），可证 △APD≌△BPC，
∴AD=BC．
由 △OPD≌△OPC，得 OC=OD，
∴OA−AD=OB+BC，得 OA=OB+2BC．
（3） 不成立，OA=2BC−OB．
【解析】作 PD⊥OA 于 D，如图 3，
∵ 点 P 在 ∠MON 的平分线上，且 PC⊥OC，
∴PC=PD，∠ADP=∠BCP=90∘，
∵∠APD+∠DPB=180∘−α=∠DPB+∠BPC，
∴∠APD=∠BPC，
∴△ADP≌△BCP，
∴AD=BC，
∴OA=OD+AD=BC+OC=2BC−OB．
24. （1） M2−0.5,2；
② 设 Ma,2a+m 在直线 y=2x+m 上，M 关于直线 AB 的对称点为 Q4−a,2a+m，
则 2≤4−a≤5，0≤2a+m≤2−a．
解得：−1≤a≤2，−4≤m≤5．
【解析】① 设直线 AD 的解析式为 y=kx+b，则：0=2k+b,3=5k+b.
解得：k=1,b=−2.
∴ 直线 AD 为：y=x−2．点 M10,3 关于直线 AB 的对称点为 Q4,3，当 x=4 时，y=x−2=2．
∵2<3，
∴Q 在 △ACD 外，
∴M1 不是 △ACD 关于直线 AB 的“反称点”；
点 M2−0.5,2 关于直线 AB 的对称点为 Q4.5,2，当 x=4.5 时，y=x−2=2.5．
∵2.5>2，
∴Q 在 △ACD 内，
∴M2 是 △ACD 关于直线 AB 的“反称点”；
点 M3−2,1 于直线 AB 的对称点为 Q6,1．
∵6>5，
∴Q 在 △ACD 外，
∴M3 不是 △ACD 关于直线 AB 的“反称点”．
（2） 易求直线 EG 的解析式为 y=3x−3．
点 Pa,a+1 在直线 y=x+1 上，P 关于直线 AB 的对称点为 Q4−a,a+1，
则 1≤4−a≤5，0≤a+1≤34−a−3．
解得：−1≤a≤5−23．
25. （1） 原式=2a2−6ab+9b2=2a−3b2．
（2） 原式=x2−4y+1x2−1=x2−4y+1x+1x−1．
26. ∵AB∥EC，
∴∠BAC=∠DCE，
在 △ABC 和 △CDE 中，
∠BAC=∠DCE,AB=CD,∠B=∠D,
∴△ABC≌△CDE（ASA）．
∴BC=DE．
27. 原式=23−2−3−22=23−2−3+22=3+2.
28. 原式= a+ba−baa−b÷a2+2ab+b2a=1a+b
在 −2①若 a=−1, 分式 a2−b2a2−ab 无意义；
②若 a=0, 分式 2ab+b2a 无意义；
③若 a=1, 分式 1a+b 无意义．
所以 a 在规定的范围内取整数，原式均无意义（或所求值不存在）．