










人教版27.2.1 相似三角形的判定一等奖课件ppt
展开学习目标1. 掌握利用两角来判定两个三角形相似的方法,并能进行相关计算. 2. 掌握判定两个直角三角形相似的方法,并能进行相关计算.
截至目前为止,相似三角形判定的方法
1. 定义法:三组对应边的比相等且对应角相等.(不常用)
2. “平行”定理:平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.
3. “三边”定理:三边成比例的两个三角形相似.
4. “两边夹角”定理:两边成比例且夹角相等的两个三角形相似.
这两个三角形的三个内角的大小有什么关系?
思考:三个内角对应相等的两个三角形一定相似吗?
观察你与老师的或与同桌的两副三角尺(30°与60°,或45°与45°) ,两个三角尺大小可能不同,会相似吗?
如果两个三角形有两组对应角相等,它们一定相似吗?
1. 作△ABC和△A'B'C',使得∠A=∠A',∠B=∠B',这时它们的第三个角满足∠C=∠C'吗?2. 分别度量这两个三角形的边长,计算 ,你有什么发现?3. △ABC和△A'B'C'相似吗?
满足:∠C = ∠C' ;
;△ABC∽ △ A'B'C'
把你的结果与同桌比较,你们的结论一样吗? △ABC和△A'B'C'相似吗?
一、两角分别相等的两个三角形相似
如图,已知△ABC和△A'B'C'中,∠A=∠A', ∠B=∠B',求证: △ABC∽ △A'B'C'
猜想:判定两个三角形相似的又一个简便方法:
两角分别相等的两个三角形相似.
【分析】证明两个三角形相似的方法: 1. 定义; 2. “平行”定理; 3. “三边”定理; 4. “两边夹角”定理.创造具备定理条件的基本图形: 在较大的三角形上截取线段,构造全等三角形.
又∵∠A=∠A',AD=A'B'
证明:在△ABC的边AB(或延长线)上,截取AD=A'B',过点D作DE//BC,交AC于点E,则有△ADE∽ △ABC.
∵∠ADE=∠B, ∠B=∠B'
∴△ADE≌△A'B'C'
∴△A'B'C'∽△ABC
由此得到利用两组角判定两个三角形相似的定理:两角分别相等的两个三角形相似.
∵ ∠A=∠A',∠B=∠B',
∴ △ABC ∽ △A'B'C'.
1. 下面每组的两个三角形是否相似?为什么?
2. 判断题:(1)所有的直角三角形都相似 . ( ) (2)所有的等边三角形都相似. ( )(3)所有的等腰直角三角形都相似. ( )(4)有一个角相等的两等腰三角形相似 . ( )
3. 如图,在 △ABC 和 △A'B'C' 中,若∠A=50°,∠B=75°,∠A' = 50°,当∠C'= 时,△ABC ∽△A'B'C'.
证明:∵ 在△ ABC中,∠A=40 ° ,∠B=80 ° , ∴ ∠C=180 °-∠A-∠B=60 °. ∵ 在△DEF中,∠E=80 °, ∠F=60 °. ∴ ∠B=∠E,∠C=∠F. ∴ △ABC ∽△DEF.
4. 如图,在△ABC 和 △DEF 中,∠A=40°,∠B=80°,∠E=80 °,∠F=60 °.求证:△ABC ∽△DEF.
5. 如果,当∠ACD满足什么条件时,△ACD∽△ABC?
答案: ∠ACD= ∠ABC.
解: ∵∠A= ∠A ,∠ABD=∠C ∴△ABD ∽ △ ACB ∴ AB : AC=AD : AB ∴ AB2 = AD · AC ∵ AD=2,AC=8 ∴ AB =4
6. 已知如图, ∠ABD=∠C,AD=2 ,AC=8,求AB.
7. 已知如图直线BE、DC交于A , ∠E= ∠C.求证:DA·AC=AB·AE
证明:∵∠E=∠C,∠DAE=∠BAC ∴△ABC ∽ △ ADE ∴ AC : AE=AB : AD ∴ DA · AC=AB · AE
例1:如图,弦 AB 和 CD 相交于 ⊙O 内一点 P,求证:PA · PB=PC · PD.证明:连接AC,DB. ∵∠A 和∠D 都是 所对的圆周角, ∴ ∠A= ∠D, 同理 ∠C= ∠B, ∴ △PAC ∽ △PDB, ∴ , 即PA ·PB = PC · PD.
1. 如图,⊙O 的弦 AB,CD 相交于点 P,若 PA=3,PB = 8,PC = 4,则 PD = .
解:(1)△DBE∽△DAB;△DBE∽△CAE;△ABD∽△AEC.(2)选择△ABD∽△AEC. ∵DA是∠BAC的平分线,∴∠BAD=∠CAE. 又∵∠D=∠C,∴△ABD∽△AEC.
2. 如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E,连接BD.(1)请你找出图中所有的相似三角形;(2)请选择其中的一对相似三角形予以证明.
3.在上题条件下,若DE=3,EA=7,则BD=______.
解:∵ ED⊥AB,∴∠EDA=90 ° . 又∠C=90 °,∠A=∠A, ∴ △AED ∽△ABC.
例2:如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求AD的长.
二、判定两个直角三角形相似
由此得到一个判定直角三角形相似的方法:有一个锐角相等的两个直角三角形相似.
思考:对于两个直角三角形,我们可以用 “HL”判定它们全等. 那么,满足斜边和一直角边成比例的两个直角三角形相似吗?
证明:设____________= k ,则AB=kA′B′,AC=kA′C′.由 ,得 ∴ ________. ∴ Rt △ABC ∽ Rt △A′B′C′.
∵ ∠C=90°,∠C′=90°, ,
由此得到另一个判定直角三角形相似的方法:斜边和一直角边成比例的两个直角三角形相似.
如图,在 Rt△ABC 和 Rt△A′B′C′ 中,
∴ Rt△ABC ∽ Rt△A′B′C′.
1. 在 Rt△ABC 和 Rt△A′B′C′ 中,∠C=∠C′=90°,依据下列各组条件判定这两个三角形是否相似.(1)∠A=35°,∠B′=55°: ;(2)AC=3,BC=4,A′C′=6,B′C′=8: ;(3)AB=10,AC=8,A′B′=25,B′C′=15: .
2. 如图,在矩形ABCD中,DE⊥AC于E,则△ABC∽△ ,△ABC∽△ ,△ABC∽△ .
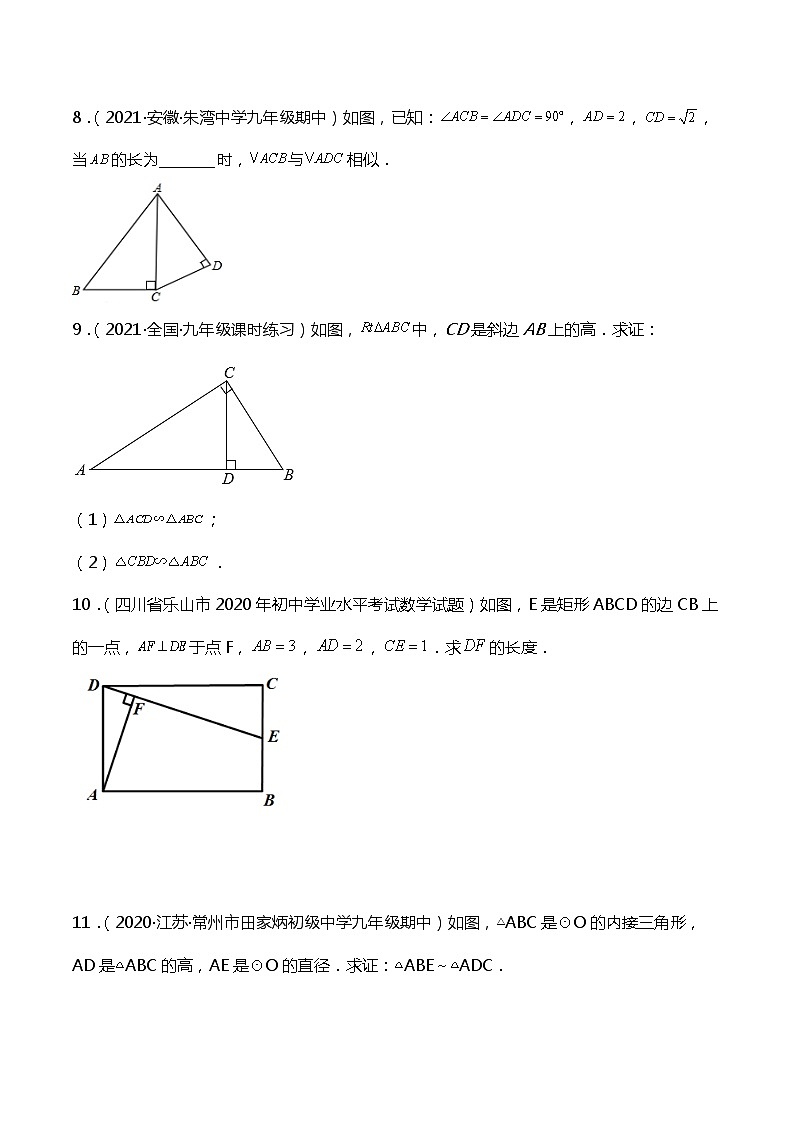
3. 如图,已知:∠ACB =∠ADC = 90°,AD = 2,CD = ,当 AB 的长为 时,△ACB 与△ADC相似.
【分析】观察得到AB和AC分别是斜边,但两条直角边的对应关系并没有确定,因此需要分类讨论.
解:∵∠ADC = 90°,AD = 2,CD = ,要使这两个直角三角形相似,有两种情况:(1)当 Rt△ABC ∽ Rt△ACD 时,有 AC : AD =AB : AC, 即 : 2 =AB : ,解得 AB=3;
(2)当 Rt△ACB ∽ Rt△CDA 时,有 AC : CD =AB : AC , 即 : =AB : ,解得 AB= .∴ 当 AB 的长为 3 或 时,这两个直角三角形相似.
如图,AD⊥BC于点D, CE⊥AB于点 E ,且交AD于F,从中找出相似的三角形?
△ACD ∽△CBD∽△ABC
找出图中所有的相似三角形.
有三对相似三角形:△ACD∽ △CBD△CBD∽ △ABC△ACD∽ △ABC
常用的相等的角: ∠A =∠DCB ;∠B =∠ACD
AC·BC=AB·CD
证两三角形相似,若已具备一组角对应相等,则应先考虑“两角分别相等的两个三角形相似”这一判定方法,而找等角时常用到公共角、对顶角、等角(或同角)的余角相等等一些隐含条件.判定直角三角形相似时,可以用其相似独有的判定方法,也可以用一般三角形相似的判定方法.不过,更多的时候是用两角相等来证.
1. 下列结论: ①所有的等腰三角形都相似, ②有一个角是80°的两个等腰三角形相似, ③有一个角是100°的两个等腰三角形相似, ④有一个角相等的两个等腰三角形相似,其中正确的有( ) A.1个B.2个 C.3个 D.4个
2. 如图,已知 AB∥DE,∠AFC =∠E,则图中相似三角形共有 ( ) A. 1对 B. 2对 C. 3对 D. 4对
3. 如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点O,若AD=1,BC=3,则 的值为 ( )
4. 如图,△ABC中,AE 交 BC 于点 D,∠C=∠E,AD : DE=3 : 5,AE=8,BD=4,则DC的长等于 ( )
5. 如图,点 D 在 AB上,当∠ =∠ (或∠ =∠ )时, △ACD∽△ABC;
6. 如图,在 Rt△ABC 中, ∠ABC = 90°,BD⊥AC于D. 若 AB=6,AD=2,则 BD= ,AC= ,BC= .
7. 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高. (1)若AD=8,BD=2,则CD= ;(2)若BD=4,AB=9,则BC= ;(3)若AD=2,AB=3,则AC= ; (4)若CD=8,BD=4,则AD= .(5)若AB=5,AC=4,则CD= .
8. (1)如图1,请你增加一个条件:∠ =∠ .(或∠ =∠ ),使△ABC∽ △ACD. (2)如图2,请你增加一个条件:∠ =∠ .(或∠ =∠ ),使△ABC∽ △AED.
9. 如图,△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.
证明: ∵ DE∥BC,EF∥AB,
∠A=∠FEC.
∴ △ADE∽△EFC.
证明:∵∠BAC= ∠1+ ∠DAC, ∠DAE= ∠3+ ∠DAC,∠1=∠3, ∴ ∠BAC=∠DAE. ∵ ∠C=180°-∠2-∠DOC , ∠E=180°-∠3-∠AOE, ∠DOC =∠AOE(对顶角相等), ∴ ∠C= ∠E. ∴ △ABC∽△ADE.
1. 如图,∠1=∠2=∠3,求证:△ABC ∽△ADE.
证明: ∵ △ABC 的高AD、BE交于点F, ∴ ∠FEA=∠FDB=90°, ∠AFE =∠BFD (对顶角相等). ∴ △FEA ∽ △ FDB, ∴
2. 如图,△ABC 的高 AD,BE 交于点 F.求证:
两角分别相等的两个三角形相似
利用两角判定三角形相似
5. “两角”定理:两角分别相等的两个三角形相似.
直角三角形相似的判定方法
在两个直角三角形中,如果有:
(2)两组直角边成比例;
(3)斜边直角边成比例;
以上任何一种情况,都能得到这两个直角三角形相似.
判定一般三角形相似的方法,都适用于判定直角三角形相似,此外:
人教版九年级下册27.2.1 相似三角形的判定教学课件ppt: 这是一份人教版九年级下册27.2.1 相似三角形的判定教学课件ppt,共28页。PPT课件主要包含了温故知新,三角形相似判定定理3,探究新知一,推导格式,知识归纳一,典型例题一,当堂训练一,探究新知二,知识归纳二,典型例题二等内容,欢迎下载使用。
初中数学人教版九年级下册27.2.1 相似三角形的判定评课课件ppt: 这是一份初中数学人教版九年级下册27.2.1 相似三角形的判定评课课件ppt,共6页。PPT课件主要包含了符号语言,相似三角形的判定,∠A∠A,∠B∠B,学以致用,问题2,谈谈收获等内容,欢迎下载使用。
九年级下册27.2.1 相似三角形的判定公开课ppt课件: 这是一份九年级下册27.2.1 相似三角形的判定公开课ppt课件,文件包含2721相似三角形的判定课件pptx、2721相似三角形的判定同步练习docx、2721相似三角形的判定教案doc等3份课件配套教学资源,其中PPT共44页, 欢迎下载使用。














