
江苏省常州市西夏墅中学高一数学教学案:《函数的表示方法》(新人教A版,必修1)
展开一、学习目标:
1.进一步理解函数的概念,了解函数表示的多样性,能熟练掌握函数的三种不同的表示方法;
2.在理解掌握函数的三种表示方法基础上,了解函数不同表示法的优缺点,针对具体问题能合理地选择表示方法;
3.通过教学,培养学生重要的数学思想方法——分类思想方法.
二、课前预复习
1.函数的概念,函数的三要素。
2. 下表的对应关系能否表示一个函数:
x | 1 | 3 | 5 | 7 |
y | -1 | -3 | 0 | 0 |
三、问题解决.
如何表示一个函数呢?
1.阅读课本掌握函数的三种常用表示方法;
2.比较三种表示法之间的优缺点.
3.完成练习
小结:
1.函数的表示方法:
2.三种不同方法的优缺点:
函数的表示方法 | 优点 | 缺点 |
|
|
|
|
|
|
|
|
|
3.三种不同方法的相互转化:能用解析式表示的,一般都能列出符合条件的表、画出符合条件的图,反之亦然;列表法也能通过图形来表示.
例1 购买某种饮料x听,所需钱数为y元.若每听2元,试分别用解析法、列表法、图象法将y表示成x(x∈{1,2,3,4})的函数,并指出该函数的值域.
跟踪练习:某公司将进货单价为8元一个的商品按10元一个销售,每天可卖出100个,若这种商品的销售价每个上涨1元,则销售量就减少10个.
(1)列表:
单价 | 10 |
|
|
|
|
|
|
|
| 20 |
数量 | 100 |
|
|
|
|
|
|
|
| 0 |
利润 | 200 |
|
|
|
|
|
|
|
| 0 |
(2)图象:
(3)解析式:
将条件变换成:“某公司将进货单价为8元一个
的商品按10元一个销售,每天可卖出110个”
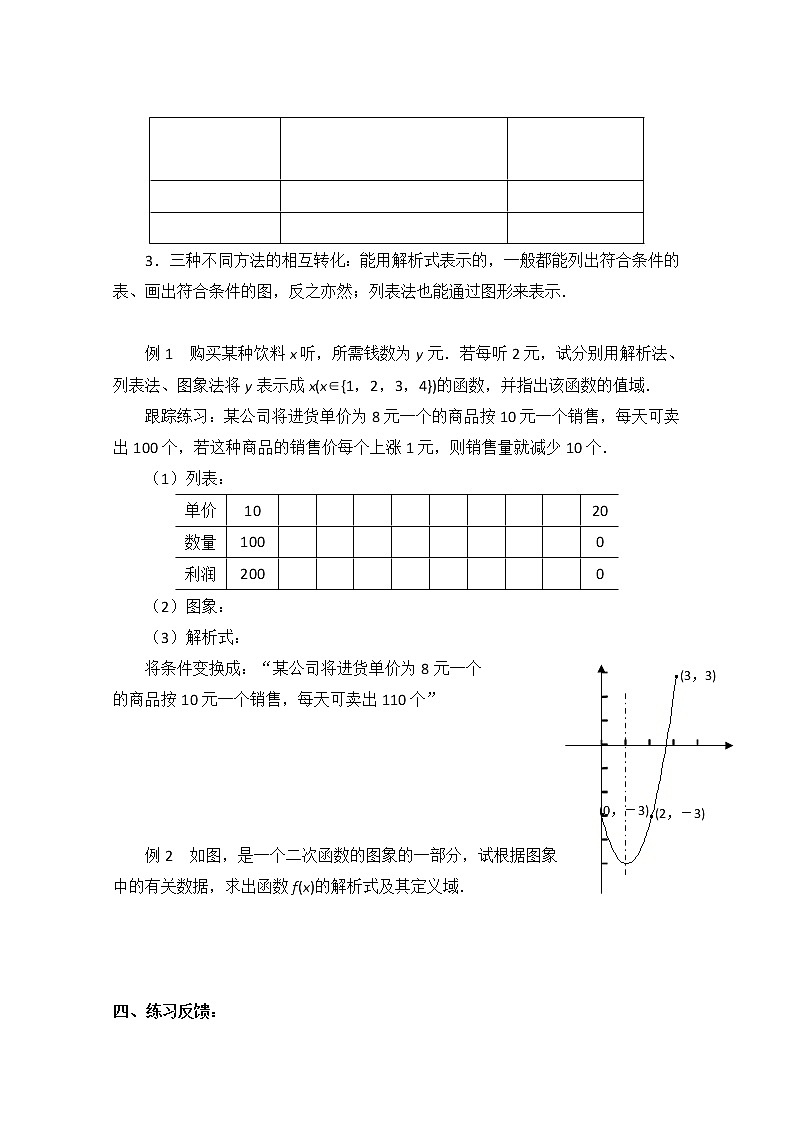
例2 如图,是一个二次函数的图象的一部分,试根据图象
中的有关数据,求出函数f(x)的解析式及其定义域.
四、练习反馈:
1.1 nmile(海里)约为1854m,根据这一关系,写出米数y关于海里数x的函数解析式.
2.用长为30cm的铁丝围成矩形,试将矩形的面积S(cm2)表示为矩形一边长x(cm)的函数,并画出函数的图象.
3.已知f(x)是一次函数,且图象经过(1,0)和(-2,3)两点,求f(x)的解析式.
4.已知f(x)是一次函数,且f(f(x))=9x-4,求f(x)的解析式.
课堂作业:课本32页1,4,5.
五、课堂小结:
六、课后巩固:
基础达标:
1.已知f(x)=,求f(0)= f[f(-1)]=
2.设函数,则=_______________________。
3.将二次函数的顶点移到后,得到的函数的解析式为_____________。
4.,的最大值是=
5.若是一次函数,且,则= _________________。
6.设函数,则 ,若,则= 。
7.已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求函数f(x)的解析式。
8.已知f(2x+1)=3x-2,求函数f(x)的解析式。(配凑法或换元法)
9.已知函数f(x)满足,求函数f(x)的解析式。(消去法)
10.已知函数=4x+3,g(x)=x, 求f[f(x)],f[g(x)],g[f(x)],g[g(x)]
11.已知 ,求函数f(x)的解析式。
能力提升:
12.已知,求函数f(x)的解析式。
13.已知,求函数f(x)的解析式。
七、学习反思:









