浙江省温州市鹿城区2021-2022学年八年级上册数学期末模拟卷（word版 含答案）

浙江省温州市鹿城区2021-2022学年八年级上册数学期末模拟卷

一、选择题(每小题3分，共30分)

1．下面四个标志中，是轴对称图形的是(   )

2．在平面直角坐标系中，点P(3，－2)关于y轴的对称点在(   )

A. 第一象限  B. 第二象限

C. 第三象限  D. 第四象限

3．使不等式x－2≥－3与2x＋3＜5同时成立的x的整数值是(    )

A. －2，－1，0  B. 0，1

C. －1，0  D. 不存在

4．一个三角形的两边长分别为3 cm和7 cm，则此三角形第三边长可能是(   )

A．3 cm  B．4 cm    C．7 cm  D．11 cm

5．为了举行班级晚会，小张同学准备去商店购买20个乒乓球做道具，并买一些乒乓球拍做奖品．已知乒乓球每个1.5元，球拍每个25元．如果购买金额不超过200元，且要求买的球拍尽可能多，那么小张同学应该买的球拍的个数是(    )

A. 5      B. 6           C. 7       D. 8

6．如图，在△ABC中，∠ACB＝90°，∠ABC＝60°，BD平分∠ABC，P是BD的中点．若AD＝6，则CP的长为(     )

A. 3  B. 3.5 

C. 4  D. 4.5

(第6题)       (第7题)

7．如图，把一张长方形纸片ABCD沿EF折叠后，点A落在CD边上的点A′处，点B落在点B′处．若∠2＝40°，则图中∠1的度数为(     )

A. 115°  B. 120°      C. 130°  D. 140°

8．在平面直角坐标系中，将直线l1：y＝－2x－2平移后，得到直线l2：y＝－2x＋4，则下列平移作法中，正确的是(      )

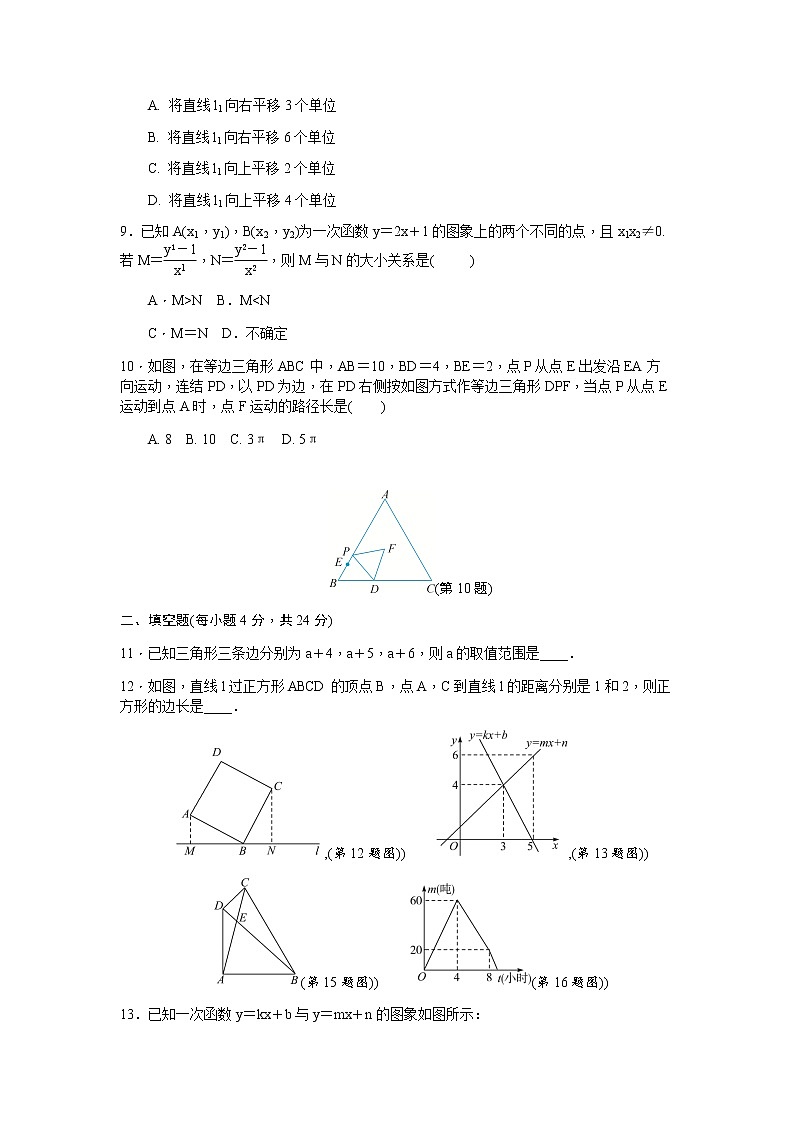
A. 将直线l1向右平移3个单位

B. 将直线l1向右平移6个单位

C. 将直线l1向上平移2个单位

D. 将直线l1向上平移4个单位

9．已知A(x1，y1)，B(x2，y2)为一次函数y＝2x＋1的图象上的两个不同的点，且x1x2≠0.若M＝，N＝，则M与N的大小关系是(     )

A．M>N  B．M<N

C．M＝N  D．不确定

10．如图，在等边三角形ABC中，AB＝10，BD＝4，BE＝2，点P从点E出发沿EA方向运动，连结PD，以PD为边，在PD右侧按如图方式作等边三角形DPF，当点P从点E运动到点A时，点F运动的路径长是(    )

A. 8  B. 10  C. 3π  D. 5π

(第10题)

二、填空题(每小题4分，共24分)

11．已知三角形三条边分别为a＋4，a＋5，a＋6，则a的取值范围是____．

12．如图，直线l过正方形ABCD的顶点B，点A，C到直线l的距离分别是1和2，则正方形的边长是____．

,(第12题图))　　,(第13题图))　　

(第15题图))　　(第16题图))

13．已知一次函数y＝kx＋b与y＝mx＋n的图象如图所示：

(1)写出关于x，y的方程组的解为____

(2)若0<kx＋b<mx＋n，写出x的取值范围是____．

14．已知关于x的方程＋1＝的解是非负数，则m的取值范围是____．

15．如图，在四边形ABCD中，对角线AC，BD相交于点E，∠DAB＝∠CDB＝90°，∠ABD＝45°，∠DCA＝30°，AB＝，则AE＝____．(提示：可过点A作BD的垂线)

16．某仓库调拨一批物资，调进物资共用8小时，调进物资4小时后同时开始调出物资(调进与调出的速度保持不变)．该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示．则这批物资从开始调进到全部调出所需要的时间是___小时．

三、解答题（本大题共7个小题，共66分）

17．（6分）解不等式（组）

（1）2（5x+3）≤x﹣3（1﹣2x）         （2）

18．（8分）已知：如图，在△ABC、△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C、D、E三点在同一直线上，连接BD．

（1）求证：△BAD≌△CAE；

（2）请判断BD、CE有何大小、位置关系，并证明．

19．（8分）如图所示，△ABC在正方形网格中，若点A的坐标为（0，3），按要求回答下列问题：

（1）在图中建立正确的平面直角坐标系，写出点B和点C的坐标；

（2）求△ABC的面积．

20．（10分）在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑摩托车从B地到A地，到达A地后立即按原路返回．如图是甲、乙两人离B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：

（1）直接写出y甲，y乙与x之间的函数关系式（不写过程）；

（2）①求出点M的坐标，并解释该点坐标所表示的实际意义；

②根据图象判断，x取何值时，y乙＞y甲．[来源:学,科,网]

21．（10分）如图，已知AC⊥BC，AD⊥BD，E为AB的中点，

（1）如图1，求证：△ECD是等腰三角形；

（2）如图2，CD与AB交点为F，若AD=BD，EF=3，DE=4，求CD的长．

22．（12分）某校八年级举行英语演讲比赛，购买A，B两种笔记本作为奖品，这两种笔记本的单价分别是12元和8元．根据比赛设奖情况，需购买笔记本共30本，并且所购买A笔记本的数量要不多于B笔记本数量的，但又不少于B笔记本数量，设买A笔记本n本，买两种笔记本的总费为w元．

（1）写出w（元）关于n（本）的函数关系式，并求出自变量n的取值范围；

（2）购买这两种笔记本各多少时，费用最少？最少的费用是多少元？

（3）商店为了促销，决定仅对A种类型的笔记本每本让利a元销售，B种类型笔记本售价不变．问购买这两种笔记本各多少本时花费最少？

23．（12分）李老师给爱好学习的小兵和小鹏提出这样一个问题：如图1，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．

小兵的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．

小鹏的证明思路是：如图2，过点P作PG⊥CF，垂足为G，先证△GPC≌△ECP，可得：PE=CG，而PD=GF，则PD+PE=CF．

请运用上述中所证明的结论和证明思路完成下列两题：

（1）如图3，将长方形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=16，CF=6，求PG+PH的值；

（2）如图4，P是边长为6的等边三角形ABC内任一点，且PD⊥AB，PF⊥AC，PE⊥BC，求PD+PE+PF的值．

参考答案

一．选择题

1-5.DCCCB

6-10.AAACA

二．填空题

11. a>－3

12.

13．     3<x<5

14.  m≤2且m≠－6

15．   2

16.   8.8_

三、解答题

17．【解答】解：（1）去括号得：10x+6≤x﹣3+6x，

移项得：10x﹣x﹣6x≤﹣3﹣6，

合并得：3x≤﹣9，

系数化为1得：x≤﹣3．

（2），

由①得：x≤1，

由②得：x＞﹣2，

∴不等式组的解集为﹣2＜x≤1．

18． 【解答】证明：（1）∵∠BAC=∠DAE=90°，

∴∠BAC+∠CAD=∠EAD+∠CAD，

∴∠BAD=∠CAE，

在△BAD和△CAE中，

，

∴△BAD≌△CAE（SAS）．

（2）BD=CE，BD⊥CE，理由如下：

由（1）知，△BAD≌△CAE，

∴BD=CE；

∵△BAD≌△CAE，

∴∠ABD=∠ACE，

∵∠ABD+∠DBC=45°，

∴∠ACE+∠DBC=45°，

∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°，

则BD⊥CE．

19．【解答】解：（1）如右图所示，

点B的坐标是（﹣3，﹣1），点C的坐标为（1，1）；

（2）由图可得，

△ABC的面积是：4×4﹣=5．

20．【解答】解：（1）设甲离B地的距离y（km）与行驶时间x（h）的函数关系式为y=kx+b，

把（0，20），（2，0）代入得：，

解得：，

∴y甲=﹣10x+20．

同法可得当0＜x≤1时，y乙=20x，当1＜x≤2时，y乙=﹣20x+40，

（2）①由，解得

∴M（，）．

表示小时时两车相遇，此时距离B地千米．

②观察图象可知：＜x＜2时，y乙＞y甲．

21．【解答】（1）证明：∵AC⊥BC，AD⊥BD，

∴∠ACB=90°，∠ADB=90°，又∵E为AB的中点，

∴CE=AB，DE=AB

∴CE=DE，即△ECD是等腰三角形；

（2）∵AD=BD，∠ADB=90°，

∴DE⊥AB，

已知DE=4，EF=3，

∴DF=5，

过点E作EH⊥CD，

∵∠FED=90°，EH⊥DF，

∴EH==，

∴DH==，

∵△ECD是等腰三角形，

∴CD=2DH=．

22． 【解答】解：（1）由题意可知：w=12n+8（30﹣n），

∴w=4n+240，

又∵A笔记本的数量要不多于B笔记本数量的，但又不少于B笔记本数量的．

∴，解得5≤n≤，

（2）w=4n+240，

∵k=4＞0，

∴w随n的增大而增大，

∴当n=5时，w取到最小值为260元．

（3）w=（12﹣a）n+8（30﹣n），

∴w=（4﹣a）n+240，

当4﹣a＞0，即a＜4时，n=5，即买A笔记本5本，B笔记本25本，花费最少，

当4﹣a=0，即a=4时，5≤n≤13，即买A笔记本5﹣13本，B笔记本25﹣17本，花费为240元，

当4﹣a＜0，即a＞4时，n=13，即买A笔记本13本，B笔记本17本，花费最少．

23．【解答】解：（1）如图3，过点E作EQ⊥BC于Q，连接BP，

∵四边形ABCD是长方形，

∴AD∥BC，

∴∠DEF=∠BFE，

由折叠可得，∠DEF=∠BEF，

∴∠BFE=∠BEF，

∴BE=BF，

∵PG⊥BE、PH⊥BC，

∴S△BEF=S△BEP+S△BFP=BE•PG+BF•PH=BF（PG+PH），

∵S△BEF=BF•EQ，

∴PG+PH=EQ，

∵四边形ABCD是长方形，

∴AD=BC，∠C=∠ADC=90°．

∵AD=16，CF=6，

∴BF=BC﹣CF=AD﹣CF=10．

由折叠易知，△DCF≌△BC'F≌△BAE，

∴C'F=CF=6，

∴C'B=AB=EQ=8；

（2）过A作AM⊥BC，连接PA，PB，PC，如图4所示：

∵△ABC为等边三角形的边长为6，AM⊥BC，

∴M为BC的中点，即BM=CM=3，

在Rt△ABM中，AB=6，BM=3，

根据勾股定理得：AM=3

又∵S△ABC=S△ABP+S△BPC+S△ACP

=PE•BC+PF•AC+PD•AB=AB（PE+PF+PD）=BC•AM，

∴（PE+PF+PD）=AM=3．