



2020-2021学年第8章 一元一次不等式8.3 一元一次不等式组教学ppt课件
展开能够根据具体问题中的数量关系,列出一元一次不等式组,解决简单问题.
渗透“数学建模”思想,提高分析问题、解决问题的能力.
一般地,关于同一个未知数的几个一元一次不等式合在一起,就组成了一个一元一次不等式组.
一元一次不等式组的定义:
1.这里的“几个”是指两个或两个以上;2.每个不等式只能是一元一次不等式;3.每个不等式必须含有同一个未知数.
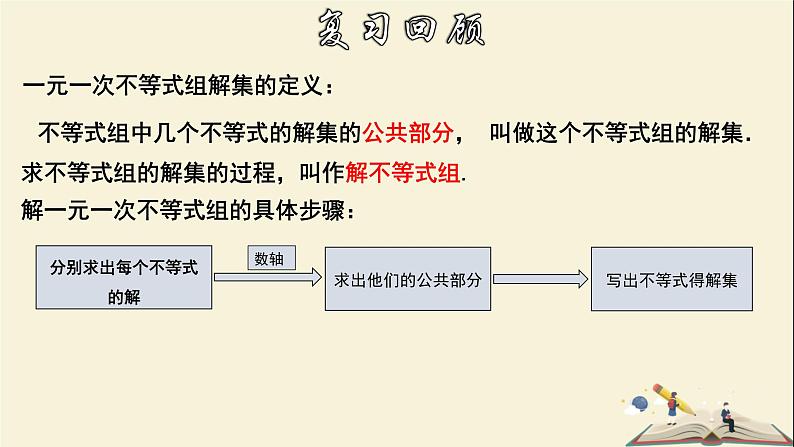
不等式组中几个不等式的解集的公共部分, 叫做这个不等式组的解集.
一元一次不等式组解集的定义:
解一元一次不等式组的具体步骤:
求不等式组的解集的过程,叫作解不等式组.
一元一次不等式组解集的四种情况:
例1:在关于x、y的方程组 中,已知x>1,y<2,求m的取值范围.
分析:先解方程组,得到x、y都是含m的代数式,再根据x>1,y<2解关于m的不等式组即可.
解不等式②,得 x<2a
所以原不等式组的解集为
因为该不等式组恰有两个整数解:0和1,
【点睛】方程组的解满足特定要求时,总是先设法求出这个方程组的解,然后根据题意列出不等式组,求出所求字母的取值范围.
因为x只能取整数,所以x=6,即有6辆汽车运这批货物.
例3:用若干辆载重量为 8 t 的汽车运一批货物,若每辆汽车只装 4 t ,则剩下 20 t 货物;若每辆汽车装满 8 t,则最后一辆汽车不满也不空.请你算一算有多少辆汽车运这批货物?
解:设有x 辆汽车,则这批货物共有(4x+20 )t.依题意得
解不等式组,得5<x <7.
(1)审:审题,分析题目中已知是什么,求什么,明确各数量之间的关系.(2)设:设适当的未知数.(3)代:用代数式表示题中的直接量和间接量.(4)列:依据不等关系列不等式(组). (5)解:求出不等式(组)的解集. (6)答:写出符合题意的答案.
列一元一次不等式(组)解应用题的一般步骤:
3个小组计划在10天内生产500件产品(每天生产量相同),按原先的生产速度,不能完成任务;如果每个小组每天比原先多生产1件产品,就能提前完成任务.每个小组原先每天生产多少件产品?
解:设每个小组原先每天生产x件产品,由题意,得
根据题意,x的值应是整数,所以x=16.
答:每个小组原先每天生产16件产品.
例4:某中学开学初到商场购买A,B两种品牌的足球,购买A品牌的足球50个,B品牌的足球25个,共花费4 500元,已知购买一个B品牌的足球比购买一个A品牌的足球多花30元.(1)求购买一个A品牌、一个B品牌的足球各需多少元.
(2)学校为了响应习总书记“足球进校园”的号召,决定再次购进A,B两种品牌足球共50个,正好赶上商场对商品价格进行调整,A品牌足球售价比第一次购买时提高4元,B品牌足球按第一次购买时售价的9折出售,如果学校此次购买A,B两种品牌足球的总费用不超过第一次花费的70%,且保证这次购买的B品牌足球不少于23个,则这次学校有哪几种购买方案?
(2)设第二次购买A品牌足球m个,则购买B品牌足球(50-m)个, 依题意得 解得25≤m≤27. 故这次学校购买足球有三种方案: 方案一:购买A品牌足球25个,B品牌足球25个; 方案二:购买A品牌足球26个,B品牌足球24个; 方案三:购买A品牌足球27个,B品牌足球23个.
(3)因为第二次购买足球时,A品牌足球单价为50+4=54(元), B品牌足球单价为80×0.9=72(元), 所以当购买方案中B品牌足球最多时,费用最高, 即方案一花钱最多. 25×54+25×72=3 150(元).答:学校在第二次购买活动中最多需要3 150元资金.
(3)请你求出学校在第二次购买活动中最多需要多少资金.
解:(1)根据题意,得
①②③的解集在数轴上表示如图
根据数轴可得不等式的解集为
∴ 8+11>0,10a+1<0.∴ |8+11|-|10a+1|=8a+11-[-(10a+1)]=18a+12.
解:①×2+②得:5x=10m-5,得:x=2m-1.①-②×2得:5y=5m+40,得:y=m+8.又∵x,y的值都是正数,且x
解:设学生有x个,则苹果有(4x+3)个,根据题意,得
解不等式组,得3.5≤x<4.5
根据题意,x的值应是整数,所以x=4,则4x+3=19.
答:学生有4人,苹果有19个.
4.某校今年冬季烧煤取暖时间为4个月.如果每月比计划多烧5吨煤,那么取暖用煤量将超过100吨;如果每月比计划少烧5吨煤,那么取暖用煤总量不足68吨.若设该校计划每月烧煤 x t,求x的取值范围.
解:根据题意,得 4(x+5)>100, ① 4(x-5)<68. ②
因此,原不等式组的解集为 20<x <22.
5.为增强居民节约用电意识,某市对居民用电实行“阶梯收费”,具体收费标准见下表:某户居民五月份用电190千瓦时,交电费90元.(1)求x和超出部分电费价格;(2)若该户居民六月份所交电费不低于75元且不超过84元,求该户居民六月份的用电量范围.
解:(1)根据题意,得160x+(190-160)(x+0.15)=90, 解得x=0.45. 则超出部分的电费价格是x+0.15=0.6(元/千瓦时),
(2)当用电量为160千瓦时时,电费为160×0.45=72(元). 因为75>72,所以该户居民六月份的用电量超过160千瓦时, 设该户居民六月份的用电量是a千瓦时,则 75≤160×0.45+0.6(a-160)≤84, 解得165≤a≤180.答:(1)x和超出部分电费价格分别是0.45元/千瓦时和0.6元/千瓦时; (2)该户居民六月份的用电量范围是165千瓦时到180千瓦时.
初中数学10.4 中心对称教学ppt课件: 这是一份初中数学10.4 中心对称教学ppt课件,共21页。PPT课件主要包含了学习目标,知识精讲,中心对称的定义,中心对称的性质,轴对称,中心对称,对比分析,典例解析,总结提升,对称中心等内容,欢迎下载使用。
初中数学华师大版七年级下册2 旋转的特征教学课件ppt: 这是一份初中数学华师大版七年级下册2 旋转的特征教学课件ppt,共15页。PPT课件主要包含了学习目标,旋转的概念,旋转的要素,旋转的特征,复习回顾,知识精讲,典例解析,达标检测,P32等内容,欢迎下载使用。
初中数学华师大版七年级下册第8章 一元一次不等式8.3 一元一次不等式组教学ppt课件: 这是一份初中数学华师大版七年级下册第8章 一元一次不等式8.3 一元一次不等式组教学ppt课件,共29页。PPT课件主要包含了学习目标,情境引入,知识精讲,③⑤⑥,典例解析,针对练习,例2解不等式组,解解不等式①得,解不等式②得,解不等式组等内容,欢迎下载使用。