必修13.2.2函数模型的应用实例课前预习课件ppt

这是一份必修13.2.2函数模型的应用实例课前预习课件ppt，共19页。PPT课件主要包含了函数模型应用实例，函数模型应用步骤，函数模型应用框图等内容，欢迎下载使用。

1．我们所学过的函数有那些？
2．你能分别说出有关这些函数的解析式、函数图象以及性质吗？
一次函数、二次函数、指数函数、对数函数以及幂函数共5种函数．
3．你能分别说说这些函数在实际生活中的应用吗？
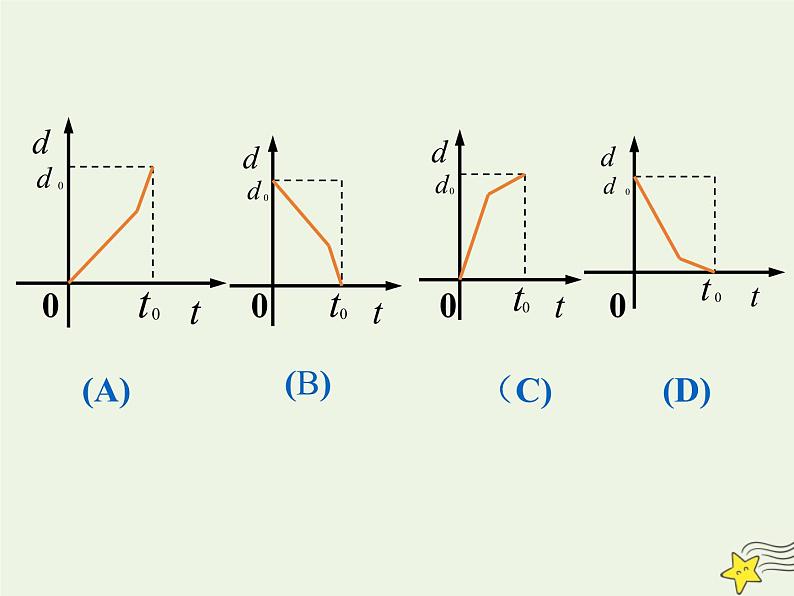
某学生早上起床太晚，为避免迟到，不得不跑步到教室，但由于平时不注意锻炼身体，结果跑了一段就累了，不得不走完余下的路程。
如果用纵轴表示家到教室的距离，横轴表示出发后的时间，则下列四个图象比较符合此人走法的是（ ）
1.下图中哪几个图像与下述三件事分别吻合得最好？请你为剩下的那个 图像写出一件事。
①我离开家不久，发现自己把作业忘在家里，于是返回家里找到作业再上学
②我骑车一路匀速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间
③我出发后，心情轻松，缓慢行进，后来为了赶时间开始加速
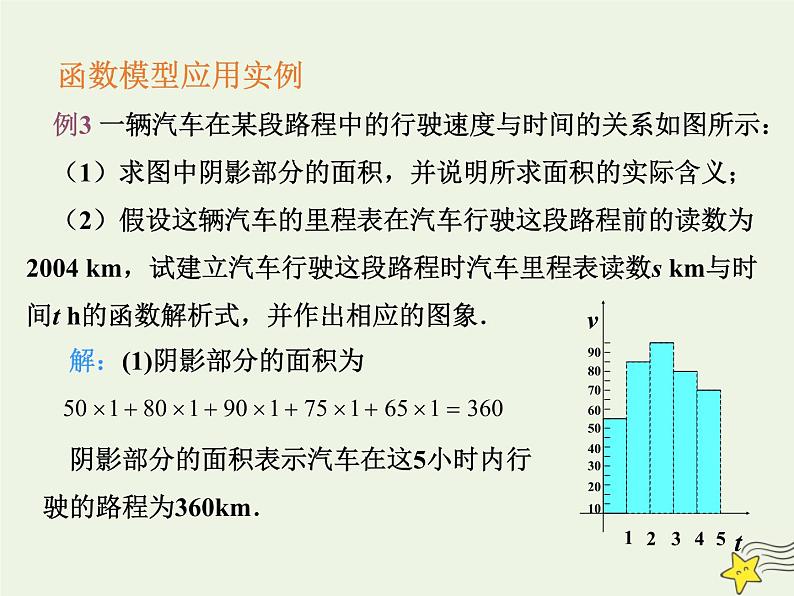
解：(1)阴影部分的面积为
阴影部分的面积表示汽车在这5小时内行驶的路程为360km．
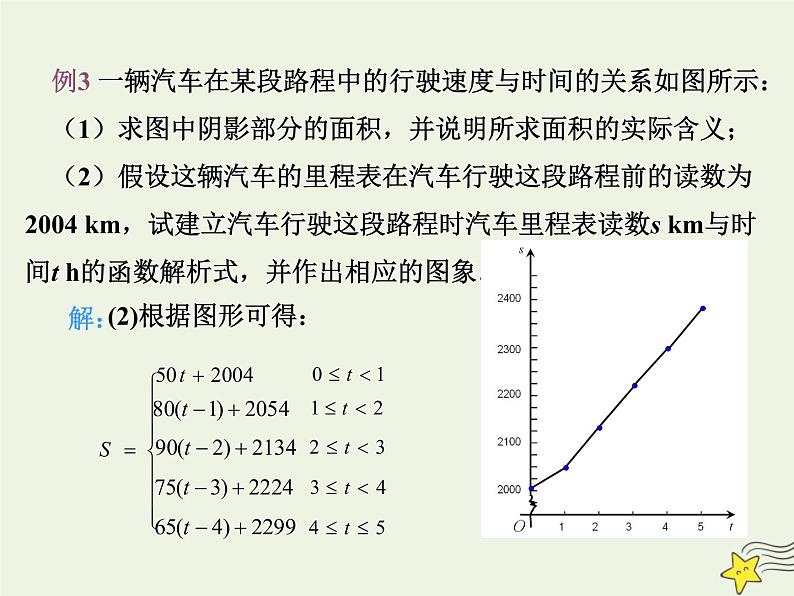
例3 一辆汽车在某段路程中的行驶速度与时间的关系如图所示： （1）求图中阴影部分的面积，并说明所求面积的实际含义； （2）假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004 km，试建立汽车行驶这段路程时汽车里程表读数s km与时间t h的函数解析式，并作出相应的图象．
(2)根据图形可得：
例4 人口问题是当今世界各国普遍关心的问题．认识人口数量的变化规律，可以为有效控制人口增长提供依据．早在1798年，英国经济学家马尔萨斯就提出了自然状态下的人口增长模型： y＝y0ert 其中t表示经过的时间，y0 表示 t＝0时的人口数，r表示人口的年平均增长率．
下表是1950～1959年我国的人口数据资料：
（1）如果以各年人口增长率的平均值作为我国这一时期的人口增长率（精确到0．0001），用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型，并检验所得模型与实际人口数据是否相符；
（2）如果按上表的增长趋势，大约在哪一年我国的人口达到13亿？
解：设1950 ～1959年的人口增长率分别为r1，r1，…r9． 经计算得我国人口在这几年得平均增长率为： r＝（r1＋r1＋…r9 ）÷9≈0.0221．
令y0＝55196，则我国在1950 ～1959年期间的人口增长模型为：
根据表中数据作出散点图．
由计算器可得：t ≈38.76．
（2）如果按上表的增长趋势，大约在哪一年我国的人口达到13亿？
所以，如果按照表中的增长趋势，那么大约在1950年后的第39年（即1989年）我国的人口就已达到13亿．由此可以看到，如果不实行计划生育，而是让人口自然增长，今天我国将面临难以承受的人口压力．
例5 某桶装水经营部每天的房租、人员工资等固定成本为200元，每桶水的进价是5元，销售单价与日均销售量的关系如表所示：
请根据以上数据作出分析，这个经营部怎样定价才能获得最大利润？
分析：由表中信息可知①销售单价每增加1元，日均销售量就减少40 桶②销售利润怎样计算较好？
解：设在进价基础上增加x元后，日均经营利润为y元，则有日均销售量为
根据收集到的数据，作出散点图，然后通过观察图象判断问题所适合的函数模型，利用计算器或计算机的数据拟合功能得出具体的函数解析式，再用得到的函数模型解决相应的问题，这是函数应用的一个基本过程．
应注意的是，用已知的函数模型刻画实际问题时，由于实际问题的条件与得到已知模型的条件会有所不同，因此往往需要对模型进行修正．
利用函数知识和函数观点解决实际问题时，一般按以下几个步骤进行：
（1）阅读理解，认真审题；
（2）引进数学符号，建立数学模型；
（3）利用数学的方法对得到的数学模型予以解答，求出结果；
（4）将数学问题的解代入实际问题进行核查．舍去不合题意的解，并作答．
用框图表示如下：