





青岛版九年级上册2.5 解直角三角形的应用备课ppt课件
展开2.4 解直角三角形(二)
已知直角三角形的两个元素(至少一个是边),熟练解直角三角形。通过将非直角三角形问题转化为解直角三角形问题,感悟转化和分类讨论的数学思想。
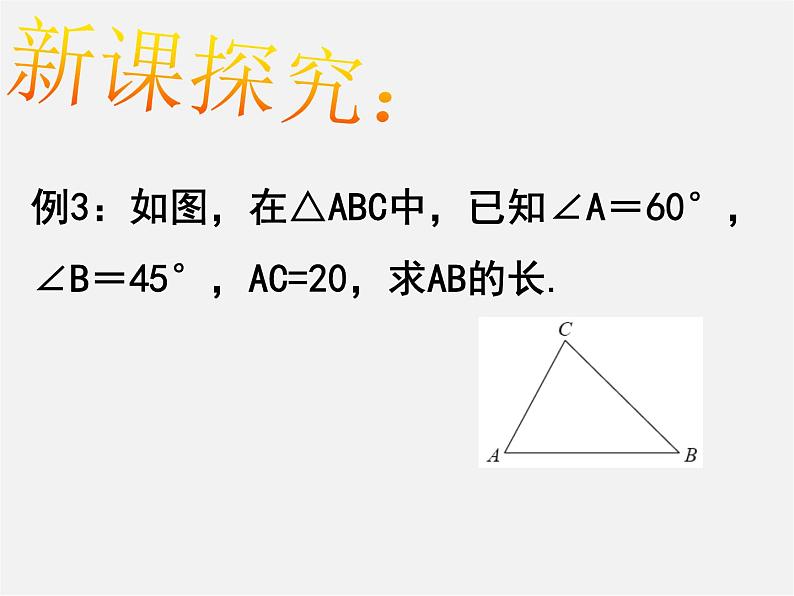
例3:如图,在△ABC中,已知∠A=60°,∠B=45°,AC=20,求AB的长.
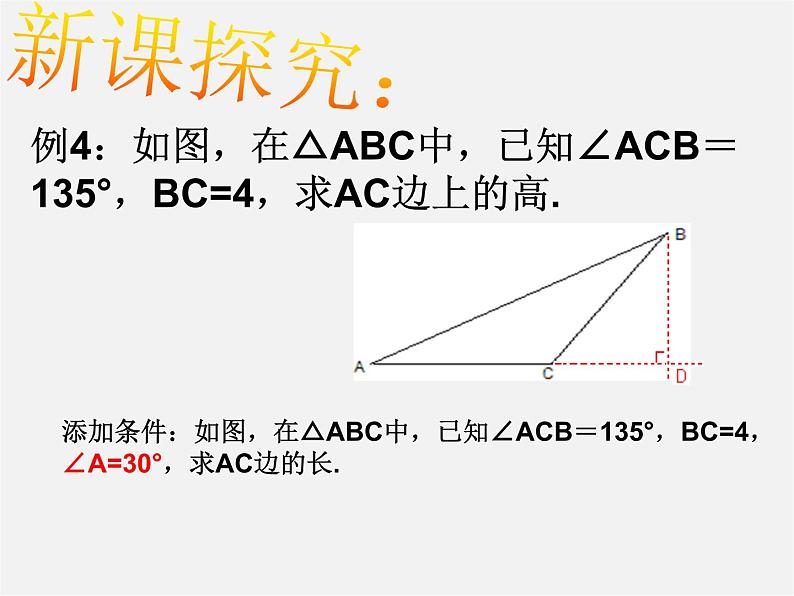
例4:如图,在△ABC中,已知∠ACB=135°,BC=4,求AC边上的高.
添加条件:如图,在△ABC中,已知∠ACB=135°,BC=4,∠A=30°,求AC边的长.
1、如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路l的距离为( )米.A.25 B. C. D.
2、如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=45°,∠ACB=30°,量得BC长为30米.求河的宽度(即求△ABC中BC边上的高);
已知等腰三角形ABC中,有一内角为30°,腰长为10cm,求等腰三角形腰上的高。
1. 如图,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,如果这时气球的高度CD为150米,且点A、D、B在同一直线上,建筑物A、B之间的距离为( )
A.150 米 B.180 米C.200 米 D.220 米
2. 山顶上有一旗杆,在地面上一点A处测得杆顶B的俯角α =600,杆底C的俯角β =450,已知旗杆高BC=20米,求山高CD。
3. 建筑物BC上有一旗杆AB,由距BC 40 m的D处观察旗杆顶部A的仰角60°,观察旗杆底部B的仰角为45°,求旗杆的高度。(保留根号)
4.如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50 m至B处,测得仰角为60°,那么该塔有多高?(小明的身高忽略不计,结果精确到1 m).
5.海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
直击中考:相信你能行! 1.(2010.潍坊)路边路灯的灯柱垂直于地面,灯杆的长为2米,灯杆与灯柱成角,锥形灯罩的轴线与灯杆垂直,且灯罩轴线正好通过道路路面的中心线(在中心线上).已知点与点之间的距离为12米,求灯柱的高.(结果保留根号)
2.(2011•潍坊)今年“五一“假期.某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点.再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°.已知A点海拔121米.C点海拔721米。(1)求B点的海拔(2)求斜坡AB的坡度.
3.(2012.潍坊)轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.A. B. C.50 D.25
4.(2012.潍坊)校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°. (1)求AB的长(精确到0.1米,参考数据: )(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.
3.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得 ,在C点测得 ,又测得 米,则小岛B到公路l的距离为多少米?
5. (2014潍坊中考) 如图,某海域有两个海拔均为200米的小岛A和小岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一小岛顶端A的俯角是45°,然后沿平行于AB的方向水平飞行1.99×104米到达D处,在D处测得正前方另一小岛顶端B的俯角是60°,求两小岛AB间的距离.
2012年5月18日,中国渔民驾驶渔船(C)在中国南海黄岩岛附近捕鱼作业时,受到外国炮艇的袭击,“中国渔政310船(A)接到陆地指挥中心(B)命令时,渔船(C)位于陆地指挥中心正南方向,位于“中国渔政310船(A)西南方向。 “中国渔政310船(A)位于陆地指挥中心(B)南偏西30°方向, ,“中国渔政310船”最大航速20海里/时,根据以上信息请你求出“中国渔政310船”赶往出事地点需要多少时间?
初中数学青岛版九年级上册2.5 解直角三角形的应用教学演示课件ppt: 这是一份初中数学青岛版九年级上册2.5 解直角三角形的应用教学演示课件ppt,共11页。PPT课件主要包含了探索新知,例题解析,巩固练习等内容,欢迎下载使用。
青岛版九年级上册2.5 解直角三角形的应用教课内容课件ppt: 这是一份青岛版九年级上册2.5 解直角三角形的应用教课内容课件ppt,共9页。PPT课件主要包含了学习目标,2边之间的关系,1角之间的关系,两条边或一边一角,温故知新,在实际测量中的角,精讲点拨,跟踪练习等内容,欢迎下载使用。
初中2.5 解直角三角形的应用说课课件ppt: 这是一份初中2.5 解直角三角形的应用说课课件ppt,共9页。













