
初中数学2.4 三角形的中位线教学课件ppt
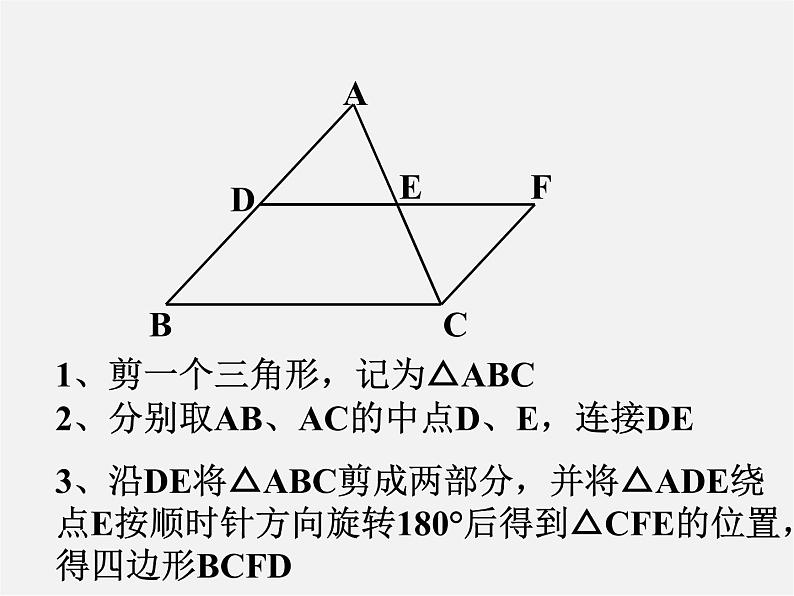
展开1、剪一个三角形,记为△ABC
2、分别取AB、AC的中点D、E,连接DE
3、沿DE将△ABC剪成两部分,并将△ADE绕点E按顺时针方向旋转180°后得到△CFE的位置,得四边形BCFD
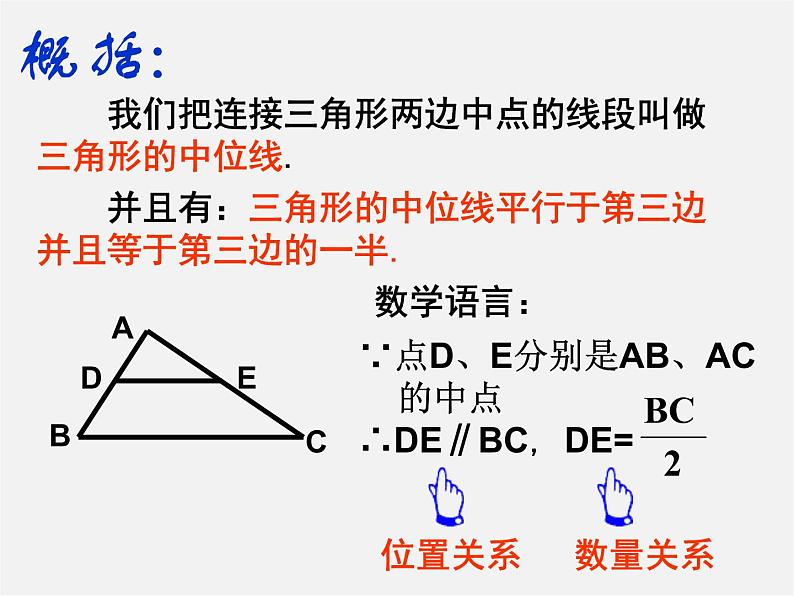
并且有:三角形的中位线平行于第三边并且等于第三边的一半.
我们把连接三角形两边中点的线段叫做三角形的中位线.
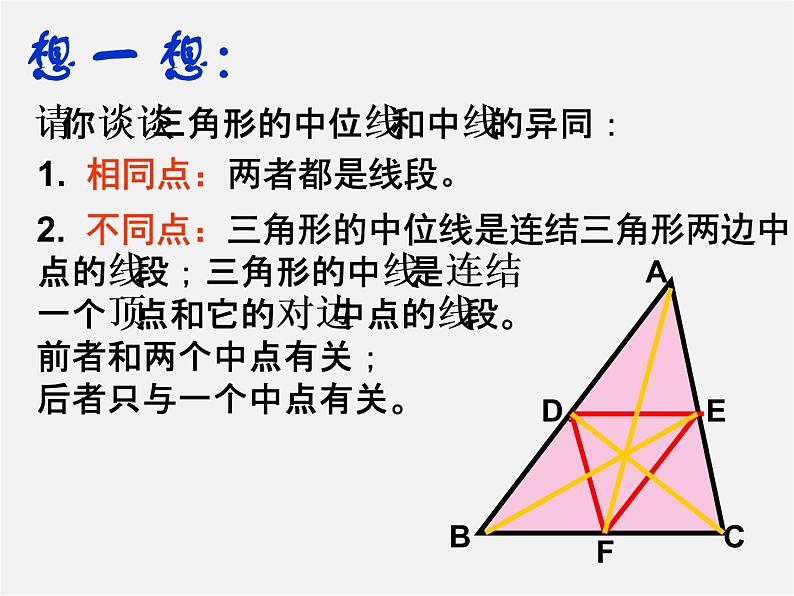
请你谈谈三角形的中位线和中线的异同:
1. 相同点:两者都是线段。
2. 不同点:三角形的中位线是连结三角形两边中点的线段;三角形的中线是连结一个顶点和它的对边中点的线段。前者和两个中点有关;后者只与一个中点有关。
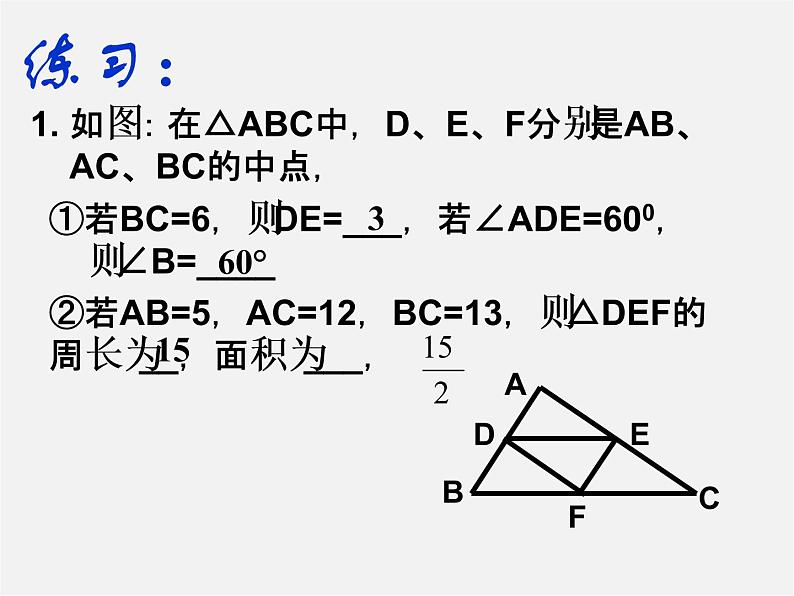
1. 如图:在△ABC中,D、E、F分别是AB、 AC、BC的中点,
①若BC=6,则DE=___,若∠ADE=600, 则∠B=____
②若AB=5,AC=12,BC=13,则△DEF的周长为__,面积为___,
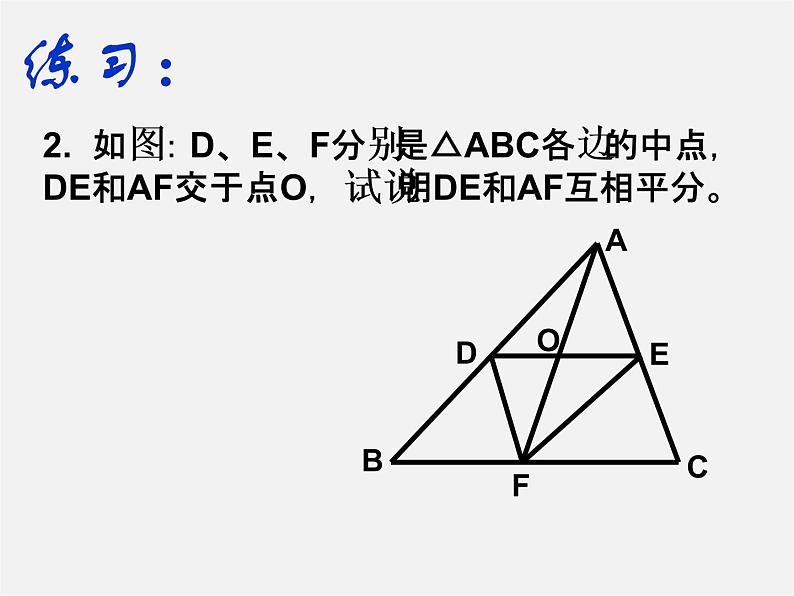
2. 如图:D、E、F分别是△ABC各边的中点,DE和AF交于点O,试说明DE和AF互相平分。
1. 如图:在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF. ①求证:EF∥BC ②若四边形BDFE的面积为6,求△ABD的面积。
“已知中点再找中点,构造中位线”是几何中常用的添加辅助线方法。
5. 如图:已知四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA边的中点,
①判断四边形EFGH是什么四边形,并证明;
②如果四边形EFGH是矩形,那么四边形ABCD应满足什么条件?
③如果四边形EFGH是菱形,那么四边形ABCD应满足什么条件?
④据上面的结论,你可得出什么结论?
(1) 顺次连接任意四边形各边中点所得的四边形是平行四边形;
关于中点四边形的结论:
6. 顺次连接以下四边形各边的中点,可以得到什么四边形?
①平行四边形, ②矩形, ③菱形④正方形,
数学八年级下册2.4 三角形的中位线课文课件ppt: 这是一份数学八年级下册2.4 三角形的中位线课文课件ppt,共13页。PPT课件主要包含了即BE∥CG,又BECG,又因为EFGF,解连结AC,答52cm等内容,欢迎下载使用。
初中数学2.1 多边形课文ppt课件: 这是一份初中数学2.1 多边形课文ppt课件,共10页。PPT课件主要包含了三角形,四边形,五边形,六边形,七边形,多边形,n-3,n-2,练兵场,细观察多思考等内容,欢迎下载使用。
湘教版八年级下册2.7 正方形课文ppt课件: 这是一份湘教版八年级下册2.7 正方形课文ppt课件,共18页。PPT课件主要包含了-------正方形,大家谈谈,正方形的性质,想一想,识别正方形的方法,合作探究等内容,欢迎下载使用。














