湘教版2.5 全等三角形授课课件ppt

这是一份湘教版2.5 全等三角形授课课件ppt，共18页。PPT课件主要包含了复习回顾，引入新课，要不重不漏哦，两边一角，两角一边，边－角－边，边－边－角，探究新知⑴，⑴边－角－边，写出结论等内容，欢迎下载使用。
全等三角形的对应边相等，对应角相等。
在上一节课我们一起探索了:
只知道两个三角形有一组或两组对应相等的元素（边或角），那么这两个三角形不一定全等．
如果只知道有三组元素对应相等,则这两个三角形全等的可能性很大.
全等三角形有性质是什么？
如果两个三角形有三组对应相等的元素（边或角），那么会有哪几种可能的情况？这时，这两个三角形一定会全等吗？
上节课我们留给大家了这样一个思考题，你们思考好了吗？
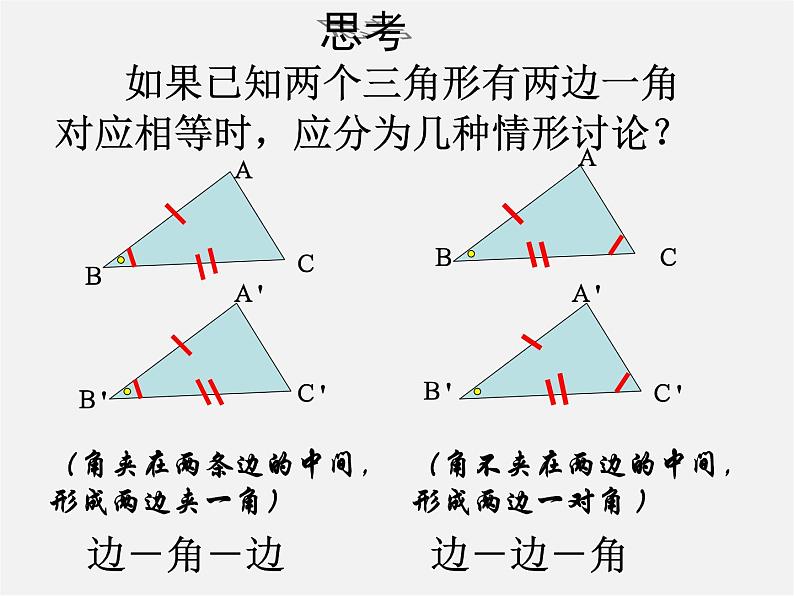
如果已知两个三角形有两边一角对应相等时，应分为几种情形讨论？
（角夹在两条边的中间，形成两边夹一角）
（角不夹在两边的中间，形成两边一对角 ）
已知两条线段和一个角，以这两条线段为边，以这个角为这两条边的夹角，画一个三角形．
步骤：　1、画一线段AB，使它等于4cm；2、画∠MAB＝45°；3、在射线AM上截取AC＝3cm；4、连结BC．△ABC即为所求．
１、请同学们把画好的三角形剪下来,并和同桌进行比较,两人的三角形全等吗?
２、小组长把本组剪好的三角形收齐并进行比较,所有的三角形全等吗?
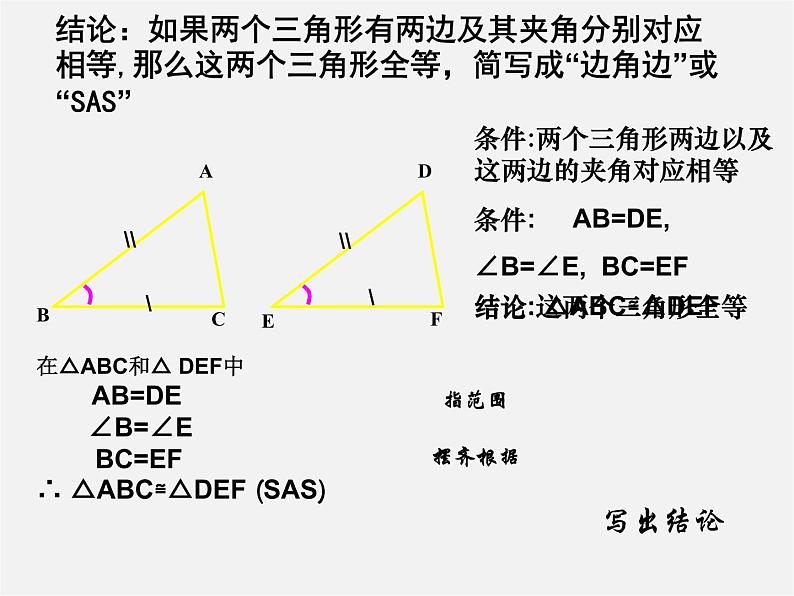
在△ABC和△ DEF中 AB=DE ∠B=∠E BC=EF∴ △ABC≌△DEF (SAS)
结论: △ABC≌△DEF
条件: AB=DE,∠B=∠E, BC=EF
结论：如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等，简写成“边角边”或“SAS”
条件:两个三角形两边以及这两边的夹角对应相等
结论:这两个三角形全等
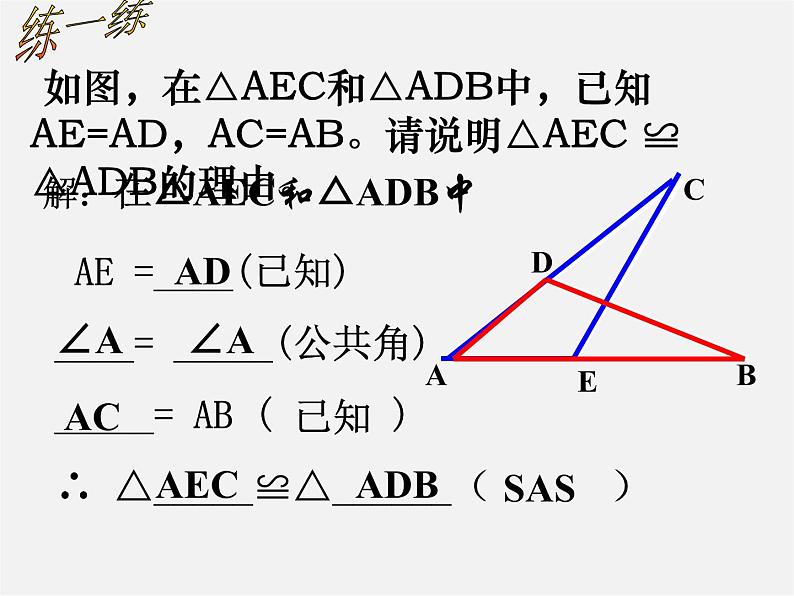
如图，在△AEC和△ADB中，已知AE=AD，AC=AB。请说明△AEC ≌ △ADB的理由。
AE =____(已知)____= _____(公共角)_____= AB ( )∴ △_____≌△______（ ）
解：在△AEC和△ADB中
如图，下列哪组条件不能判定△ABC≌△DEF（ ）
AB=DEA、∠A=∠D AC=DF
AC=DFC、∠C=∠F BC=EF
AB=DEB、∠B=∠E BC=EF
AC=DFD、∠B=∠E BC=EF
以3cm、4cm为三角形的两边，长度3cm的边所对的角为45° ，情况又怎样？动手画一画，你发现了什么？
1.画一线段AC,使它等于4cm; 2.画∠ CAM= 45°;3.以C为圆心, 3cm长为半径画弧,交AM于点B;4.连结CB. △ ABC 与 △ AB'C 就是所求做的三角形 .
显然： △ ABC与△ AB'C不全等
结论：两边及其一边所对的角相等，两个三角形不一定全等.
例1如图，在△ABC中，AB＝AC，AD平分∠BAC，求证：△ABD≌△ACD．
∴　∠BAD＝∠CAD
∴△ABD≌△ACD（SAS）
在△ABD与△ACD中
由△ABD≌△ACD ，还能证得∠B＝∠C，即证得等腰三角形的两个底角相等这条定理．
1、如图，在△ABC中，AB＝AC，AD平分∠BAC，求证： ∠B＝∠C ．
∴∠B＝∠C（全等三角形的对应角相等）
利用“SAS”和“全等三角形的对应角相等”这两条公理证明了“等腰三角形的两个底角相等”这条定理。
若题目的已知条件不变，你还能证得哪些结论？
∴ ∠ADB＝ ∠ADC （全等三角形的对应角相等）又∵ ∠ADB+ ∠ADC＝180° ∴ ∠ADB＝ ∠ADC＝ 90° ∴ AD⊥BC
2、如图，在△ABC中，AB＝AC，AD平分∠BAC，求证： ．
∴BD＝CD（全等三角形的对应边相等）
这就说明了点D是BC的中点，从而AD是底边BC上的中线。
这就说明了AD是底边BC上的高。
因铺设电线的需要，要在池塘两侧A、B处各埋设一根电线杆（如图），因无法直接量出A、B两点的距离，现有一足够的米尺。请你设计一种方案，粗略测出A、B两杆之间的距离。。
小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结CD，用米尺测出DE的长，这个长度就等于A，B两点的距离。请你说明理由。
AC=DC  ∠ACB=∠DCE BC=EC
△ACB≌△DCE（SAS）
在△ABC和△ DEC中
根据题目条件，判断下面的三角形是否全等．（1）　AC＝DF，∠C＝∠F，BC＝EF；（2）　BC＝BD，∠ABC＝∠ABD．
2.点M是等腰梯形ABCD底边AB的中点，求证： △AMD≌△BMC ．
在等腰梯形ABCD中，AB∥DC AD=BC ∠A＝∠B∵点M是底边AB的中点∴ AM=BM
　　在△ADM和△BCM中
AD＝BC∠A＝∠BAM＝BM
∴△AMD≌△BMC (SAS)