人教版九年级上册第二十三章 旋转23.1 图形的旋转第1课时测试题

23.1 图形的旋转

第 1 课时 图形的旋转

1.将数字“6”旋转 180°,得到数字“9”;将数字“9”旋转 180°,得到数字“6”.现将数字“69”旋转 180°,得到的

2. 如图,已知△OAB 是正三角形,OC⊥OB,OC=OB,将△OAB 绕点 O 按逆时针方向旋转,使得 OA 与 OC

重合,得到△OCD,则旋转的角度是( )

A.150° B.120° C.90° D.60°

3. 如图,在△ABC 中,∠C=90°,AC=4,BC=3,将△ABC 绕点 A 逆时针旋转,使点 C 落在线段 AB 上的点 E

处,点 B 落在点 D 处,则 B,D 两点间的距离为( )

A.  10 B.2  2 C.3 D.2 5

4. 如图,将△ABC 绕点 C 顺时针旋转,使点 B 落在 AB 边上点 B'处,此时,点 A 的对应点 A'恰好落在 BC

边的延长线上,下列结论错误的是( )

A.∠BCB'=∠ACA' B.∠ACB=2∠B C.∠B'CA=∠B'AC

D.B'C 平分∠BB'A'

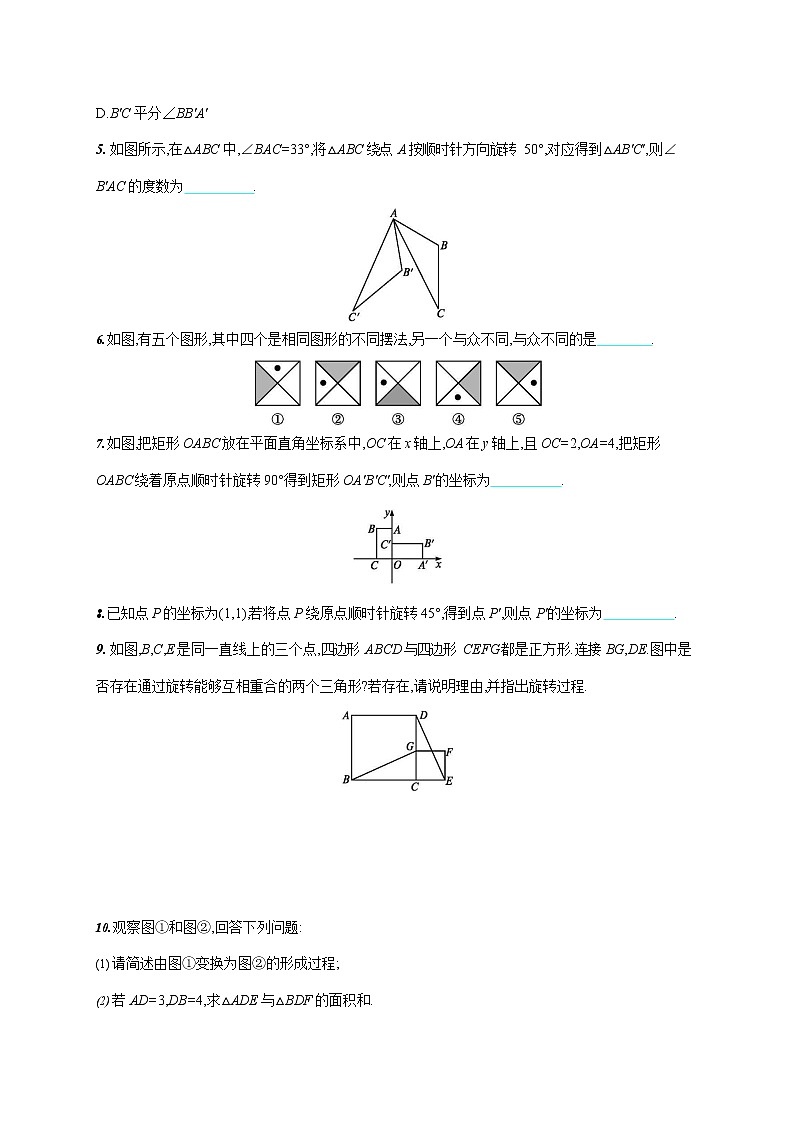
5. 如图所示,在△ABC 中,∠BAC=33°,将△ABC 绕点 A 按顺时针方向旋转 50°,对应得到△AB'C',则∠

B'AC 的度数为        .

6. 如图,有五个图形,其中四个是相同图形的不同摆法,另一个与众不同,与众不同的是        .

7. 如图,把矩形 OABC 放在平面直角坐标系中,OC 在 x 轴上,OA 在 y 轴上,且 OC=2,OA=4,把矩形OABC 绕着原点顺时针旋转 90°得到矩形 OA'B'C',则点 B'的坐标为               .

8. 已知点 P 的坐标为(1,1),若将点 P 绕原点顺时针旋转 45°,得到点 P',则点 P'的坐标为       .

9. 如图,B,C,E 是同一直线上的三个点,四边形 ABCD 与四边形 CEFG 都是正方形.连接 BG,DE.图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说明理由,并指出旋转过程.

10. 观察图①和图②,回答下列问题:

(1) 请简述由图①变换为图②的形成过程;

(2) 若 AD=3,DB=4,求△ADE 与△BDF 的面积和.

11. 如图,将△ABC 绕点 B 顺时针旋转 60°得到△DBE,点 C 的对应点 E 恰好落在 AB 的延长线上,连接

AD.下列结论一定正确的是( )

A.∠ABD=∠E B.∠CBE=∠C C.AD∥BC D.AD=BC

12. 如图,网格纸上正方形小格的边长为 1,图中线段 AB 和点 P 绕着同一个点做相同的旋转,分别得到线段 A'B'和点 P',则点 P'所在的单位正方形区域是(              )

区 B.2 区 C.3 区 D.4 区

13. 如图,在Rt△ABC 中,∠ACB=90°,∠BAC=60°,AB=6.Rt△AB'C'可以看成是由Rt△ABC 绕点 A 按逆时针方向旋转 60°得到的,则线段 B'C 的长为               .

14. 如图,△ABC≌△DEF.△DEF 能否由△ABC 通过一次旋转得到?若能,请用直尺和圆规画出旋转中心; 若不能,试简要说明理由.

★15.如图.

(1) △ABC 按照逆时针方向转动一个角度后成为△AB'C',∠CAC'=90°,图中哪一点是旋转中心?旋转了多少度?

(2) 以点 C'为旋转中心,顺时针旋转(1)问中相同的角度,那么线段 AC 与 A″C',BC 与 B″C',AB 与 A″B″有怎样的关系?B'C'与 B″C'的位置关系呢?

★16.如图,方格中每个小正方形的边长都是单位 1,△ABC 在平面直角坐标系中的位置如图.

(1) 画出将△ABC 向右平移 2 个单位得到的△A1B1C1;

(2) 画出将△ABC 绕点 O 顺时针方向旋转 90°得到的△A2B2C2.

参考答案

夯基达标

1.B 2.A

3.A 由题意可知在△ABC 中 AB 为斜边,易得 AB=5,由图形的旋转可知△ABC≌△ADE,所以AC=AE=4,DE=BC=3.而 AB=5,所以 EB=AB-AE=5-4=1.连接 DB,易得△DEB 为直角三角形,所以BD= � � 2 + � � 2 = 12 + 32 = 10. 故 选 A.

4.C 根据旋转的性质得,∠BCB'和∠ACA'都是旋转角,则∠BCB'=∠ACA',故 A 正确;

∵CB=CB',

∴∠B=∠BB'C.

又∠A'CB'=∠B+∠BB'C,

∴∠A'CB'=2∠B.

又∠ACB=∠A'CB',

∴∠ACB=2∠B,故 B 正确;

∵∠A'B'C=∠B,

∴∠A'B'C=∠BB'C,

∴B'C 平分∠BB'A',故 D 正确;故选 C.

5.17° 由题意易知∠B'AB 为旋转角,∠B'AB=50°,

∵∠BAC=33°,

∴∠B'AC=50°-33°=17°.

故答案为 17°.

6.② 将图②③④⑤均绕各自对角线的交点旋转,使其含有黑点的三角形向上,此时图③④⑤与图①  完全相同,只有图②的阴影在含黑点的三角形的右侧.

7.(4,2)

8.( 2,0)

9. 解 存在,△BCG 和△DCE.

理由:因为四边形 ABCD 和四边形 CEFG 都是正方形,所以 GC=CE,BC=CD,∠BCG=∠DCE=90°.

所以△BCG≌△DCE.所以△BCG 绕点 C 顺时针方向旋转 90°后能与△DCE 重合.

10. 解 (1)把△ADE 绕点 D 逆时针旋转 90°得到△DA1F,即由图①变换为图②.

(2)由题意,得∠A1DB=90°,A1D=AD=3,DB=4,所以� △

+ � △

= � △� � � = 1×3×4=6.

� � � � � � 1 2

培优促能

11.C ∵△ABC 绕点 B 顺时针旋转 60°得△DBE,

∴∠ABD=∠CBE=60°,AB=BD,

∴△ABD 是等边三角形,

∴∠DAB=60°,

∴∠DAB=∠CBE,

∴AD∥BC,故选 C.

12.D 如图,连接 AA',BB',分别作 AA',BB'的中垂线,两直线的交点即为旋转中心,

由图可知,线段 AB 和点 P 绕着同一个点逆时针旋转 90°,点 P 逆时针旋转 90°后所得对应点 P'落在 4

区,故选 D.

13.3  7 如图,连接 BB'.在 Rt△ABC 中,∠ABC=90°-60°=30°,所以 AC=1AB=3.

根据勾股定理,得

BC= � � 2-� � 2=3 3.

根据旋转的性质知,B'C'=BC=3 3,AC'=AC=3,∠B'C'B=90°.

所以 BC'=AB-AC'=3.

在 Rt△B'C'B 中 ,BB'= � '� '2 + � � '2=6.

由题易知∠B'BC 是直角,

所以在 Rt△B'BC 中,B'C= � � '2 + � � 2=3 7.

14. 解 能.如图,点 O 就是所求作的旋转中心.

15. 解 (1)点 A 是旋转中心,旋转了 90°. (2)AC∥A″C',且 AC=A″C';

BC∥B″C',且 BC=B″C';AB∥A″B″,且 AB=A″B″.B'C'⊥B″C'.

创新应用

16. 解 (1)如图所示. (2)如图所示.