两个三角形相似的判定PPT课件免费下载

浙教版初中数学九年级上册课文《两个三角形相似的判定》,完整版PPT课件免费下载，优秀PPT背景图搭配，精美的免费ppt模板。轻松备课，欢迎免费下载使用。

一、【课程的主要内容】

ASA AAS SAS SSS
两边对应成比例,且夹角相等的两个三角形相似吗?
相似三角形的判定1:有两个角对应相等的两个三角形相似。
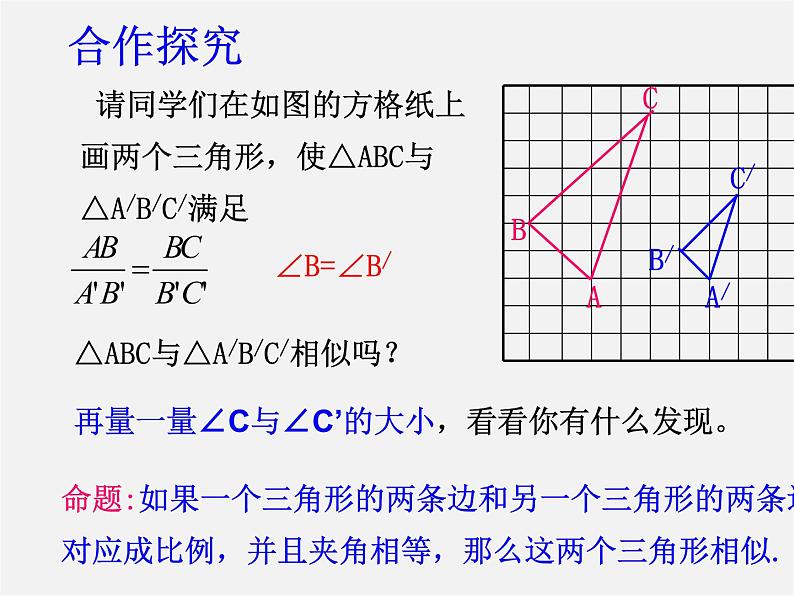
再量一量∠C与∠C’的大小，看看你有什么发现。
△ABC与△A/B/C/相似吗？
命题:如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似.
两边对应成比例,且夹角相等的两个三角形相似.
三边对应成比例的两个三角形相似.
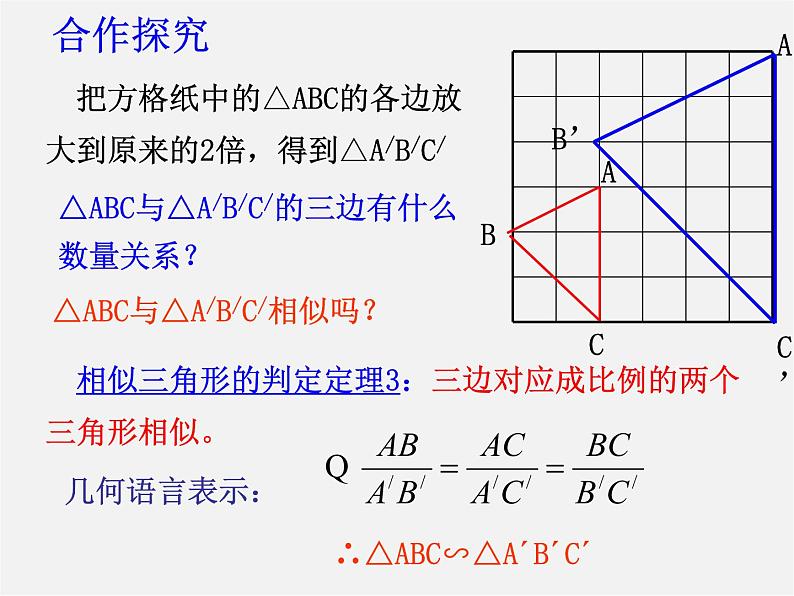
把方格纸中的△ABC的各边放大到原来的2倍，得到△A/B/C/
相似三角形的判定定理3：三边对应成比例的两个三角形相似。
△ABC与△A/B/C/的三边有什么数量关系？
∴△ABC∽△A´B´C´
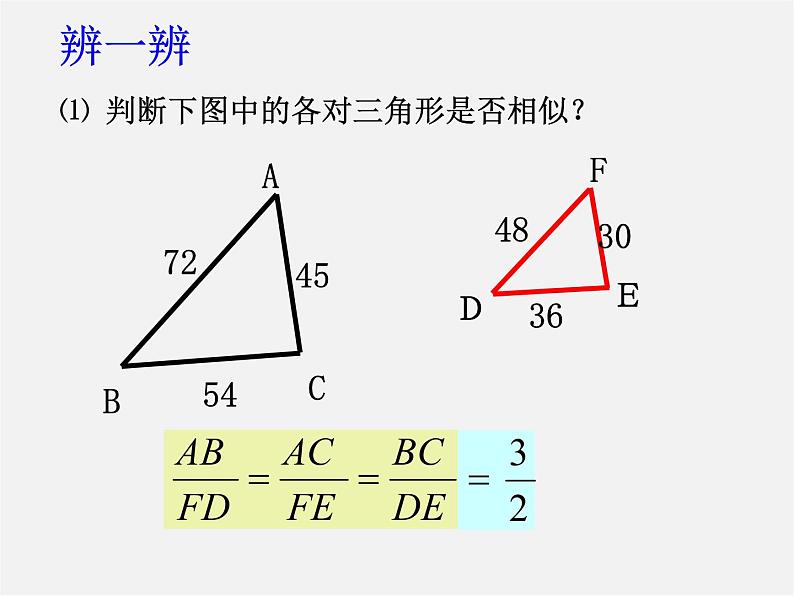
⑴ 判断下图中的各对三角形是否相似？
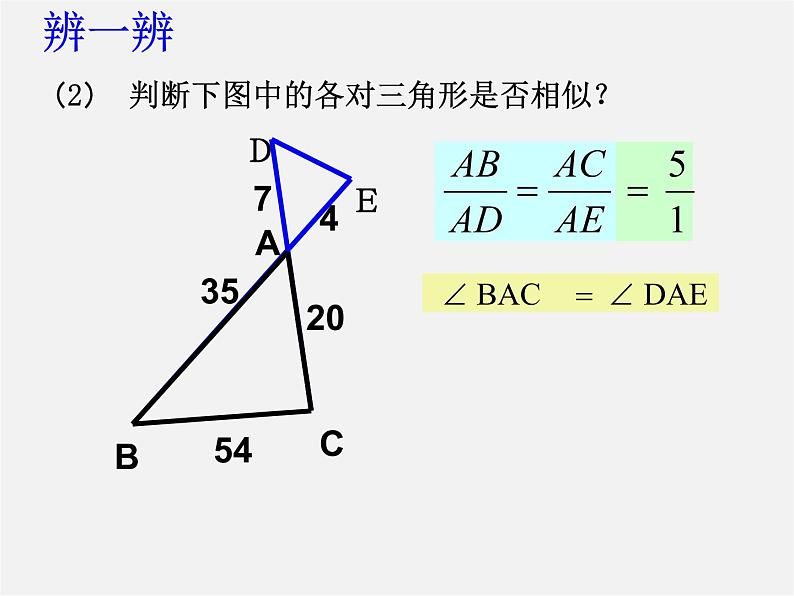
（2） 判断下图中的各对三角形是否相似？
（4）判断图中的各对三角形是否相似。
方法一：设小正方形的边长为1，则比较容易计算三边的长度，然后寻找三边的对应关系；
方法二：仔细观察不难发现图中的∠BAC和∠DEF都是直角，那么能否从两边一夹角的角度考虑并证明。

二、【典例分析】

例2、如图判断4×4方格中的两个三角形是否相似,并说明理由.
解：根据勾股定理，得：
(相似三角形的判定定理3)
D是△ABC边AB上一点，⑴若AC2=AD·AB ，△ABC与△CAD相似吗?为什么?⑵若△BCD∽△BAC,需补充什么条件?

三、【课堂练习】

1、如图：在△ABC中，D，E分别为AB、AC上的点，若AD=4，BD=3.5，AE=5，EC=1，则下列结论错误的是（ ）
A、1.5DE=BCB、△ABC∽△AEDC、∠ADE=∠B D、∠AED=∠B
2、如图,D为△ABC的边AB上一点.若使△ACD与△ABC相似,可添加一个什么条件?你有几种添加条件的不同方法?
方法一:添加一个角相等
方法二:添加两边对应成比例
如 ∠ADC=∠ACB 或 ∠ACD=∠B
或 AC2=AD·AB
3、在直角梯形BACD中,AC⊥CD,AC=CD=4AB, E是AC中点.求证:△ABE∽△CED

四、【拓展学习】

变式练习:若AB=2,E是线段AC上的一个动点, △ABE与△CED相似,求AE的长.
在有平行横线的练习本上画一条线段AB,使线段的两端点A,B恰好在两条平行线上,线段AB就被平行线分成了相等的三小段.你能说出这一事实的数学原理吗?如果只给你圆规和直尺,你会把任意一条线段AB五等分吗?请试一试,并说明你的画法的依据.