北师大版八年级上册3 勾股定理的应用授课ppt课件

这是一份北师大版八年级上册3 勾股定理的应用授课ppt课件，共18页。PPT课件主要包含了8cm等内容，欢迎下载使用。

用拼图法验证勾股定理的基本思想：构造一个图形，利用两种方法计算该图的____，从而得到一个关于三边长a，b，c之间的等式．关键是借助于图形的____来验证，依据对图形进行割补、拼接前后____不变的原理．一般拼图的方式有两种：一种是拼为正方形，另一种是拼为直角梯形．
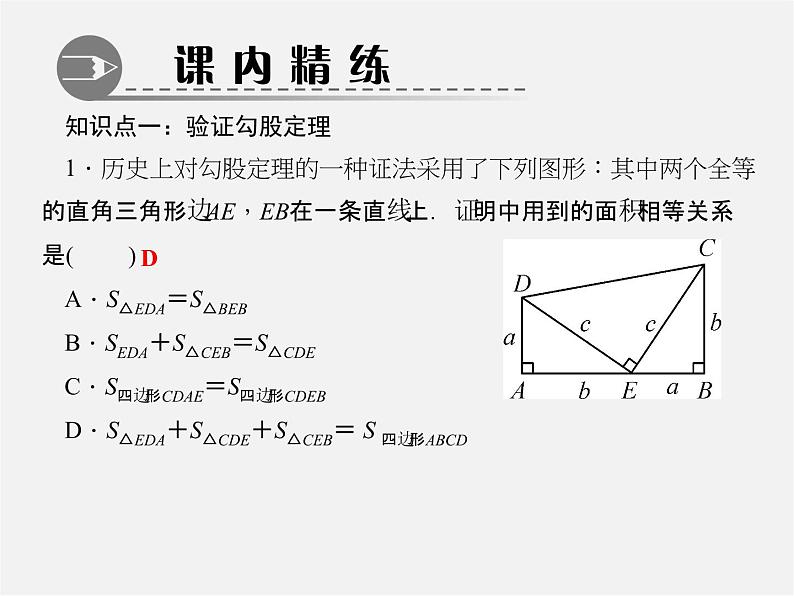
知识点一：验证勾股定理1．历史上对勾股定理的一种证法采用了下列图形：其中两个全等的直角三角形边AE，EB在一条直线上．证明中用到的面积相等关系是( )A．S△EDA＝S△BEBB．SEDA＋S△CEB＝S△CDEC．S四边形CDAE＝S四边形CDEBD．S△EDA＋S△CDE＋S△CEB＝ S 四边形ABCD
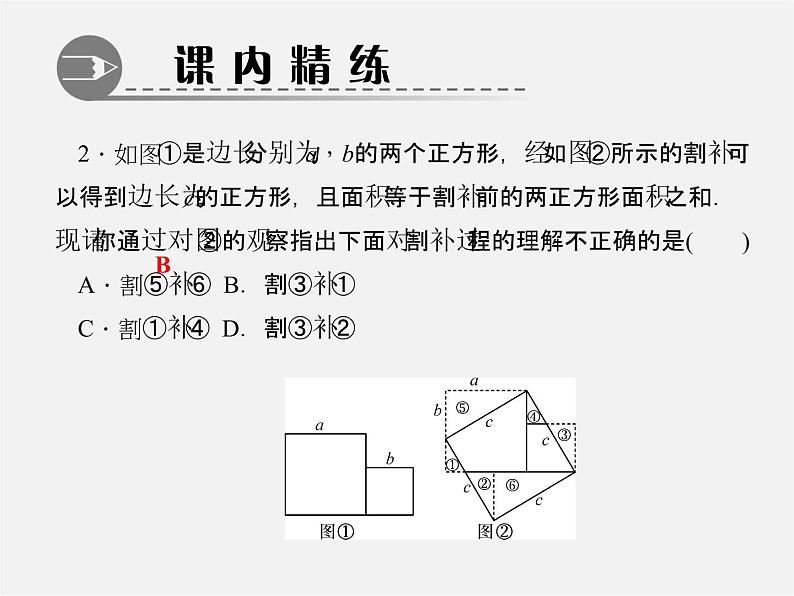
2．如图①是边长分别为a，b的两个正方形，经如图②所示的割补可以得到边长为c的正方形，且面积等于割补前的两正方形面积之和．现请你通过对图②的观察指出下面对割补过程的理解不正确的是( )A．割⑤补⑥ B．割③补①C．割①补④ D．割③补②
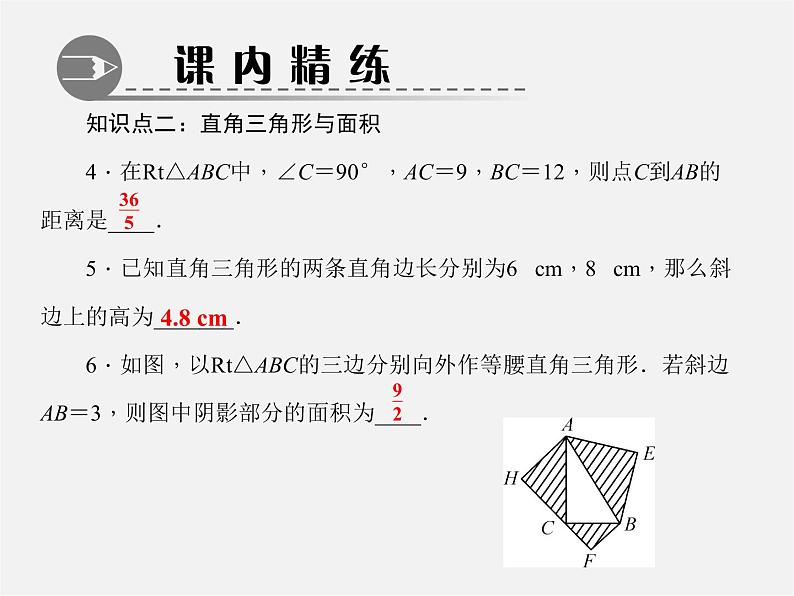
3．如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4.若用x，y表示直角三角形的两直角边(x>y)，请观察图案，指出以下关系式中不正确的是( )A．x2＋y2＝49B．x－y＝2C．2xy＋4＝49D．x＋y＝13
7．如图，在△ABC中，AB＝AC＝5，BC＝6，点E，F是中线AD上的两点，则图中阴影部分的面积是( )A．6 B．12 C．24 D．308．为了迎接新年的到来，同学们做了许多拉花布置教室，准备召开新年晚会，小王搬来一架长为2.5米的木梯，准备把梯子架到2.4米高的墙上，则梯脚与墙角的距离为( )A．0.7米 B．0.8米C．0.9米 D．1.0米
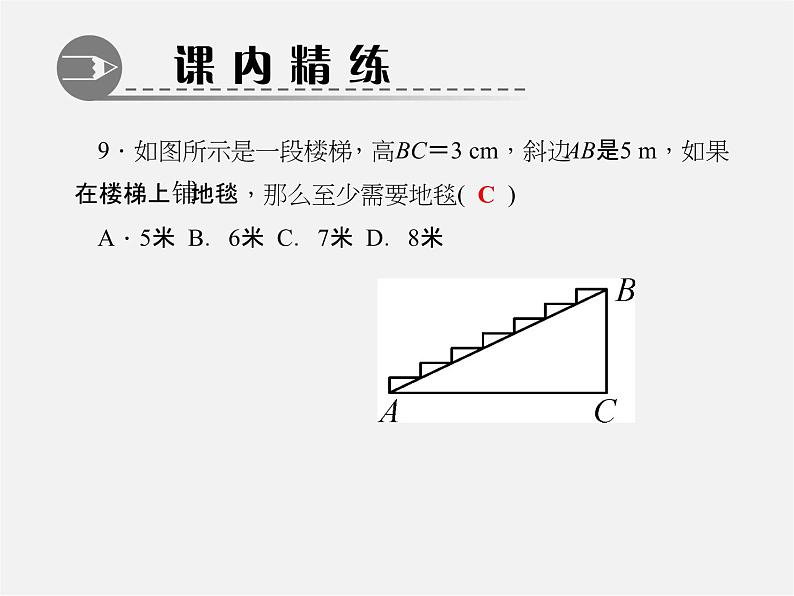
9．如图所示是一段楼梯，高BC＝3 cm，斜边AB是5 m，如果在楼梯上铺地毯，那么至少需要地毯( )A．5米 B．6米 C．7米 D．8米
10．如图，一个透明的圆柱形状的玻璃杯，由内部测得其底面半径为3 cm，高为8 cm，今有一支12 cm的吸管任意斜放于杯中，若不考虑吸管的粗细，吸管露出杯口长度最少为____cm.
11．如图，小李准备建一个蔬菜大棚，棚宽4 m，高3 m，长20 m，棚的斜面用塑料薄膜遮盖，不计墙的厚度，请你帮他计算阳光透过的最大面积．
解：在直角三角形中，由勾股定理可得，直角三角形的斜边长为5 m，所以长方形塑料薄膜的面积是5×20＝100(m2)．即阳光透过的最大面积是100 m2　
12．如图，某人欲垂直横渡一条河，由于水流的影响，他实际上岸地点C偏离了想要到达的B点140米(即BC＝140米)，其结果是他在水中实际游了500米(即AC＝500米)，则该河AB处的宽度是____米．
13．如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为( )
A．4 B．6 C．16 D．55
14．如图，隔湖有两点A，B，从与BA方向成直角的BC方向上的点C，测得CA＝50米，CB＝40米，求：(1)A，B两点间的距离；(2)点B到直线AC的距离．
15．用如图①所示的4个形状、大小完全一样的直角三角形拼一拼，摆一摆，可以摆成如图②所示的正方形，你能利用这个图形验证勾股定理吗？
16．(2015·长沙改编)为了向建国六十四周年献礼，某校各班都在开展丰富多彩的庆祝活动，八(3)班开展了手工制作竞赛，每个同学都在规定时间内完成一件手工作品．陈莉同学制作手工作品的第一、二个步骤如下：①先裁下了一张长BC＝20 cm，宽AB＝16 cm的长方形纸片ABCD，②将纸片沿着直线AE折叠，点D恰好落在BC边上的点F处，…，请你根据①②步骤解答下列问题：(1)找出图中∠FEC的余角；(2)计算EC的长．
解：(1)∠CFE，∠BAF　(2)设EC＝x cm，则EF＝DE＝(16－x)cm.又AF＝AD＝20 cm，在Rt△ABF中，由AF2＝BF2＋AB2，得BF＝12 cm.所以FC＝BC－BF＝20－12＝8(cm)．在Rt△EFC中，EF2＝FC2＋EC2.即(16－x)2＝82＋x2.解得x＝6.所以EC的长为6 cm　
17．为了丰富少年儿童的业余文化生活，某社区要在如图的AB所在的直线上建一图书阅览室．该社区有两所学校，所在的位置在点C和点D处，CA⊥AB于点A，DB⊥AB于点B.已知AB＝25 km，CA＝15 km，DB＝10 km.试问：阅览室E建在距点A多少千米处，才能使它到C，D两所学校的距离相等．