数学第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定多媒体教学ppt课件

这是一份数学第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定多媒体教学ppt课件，共14页。PPT课件主要包含了∠A∠A1，∠B∠B1，∠C∠C1，CDC1D1，新知应用，∴AD225，∴BD075，EF∥BC，课堂小结等内容，欢迎下载使用。
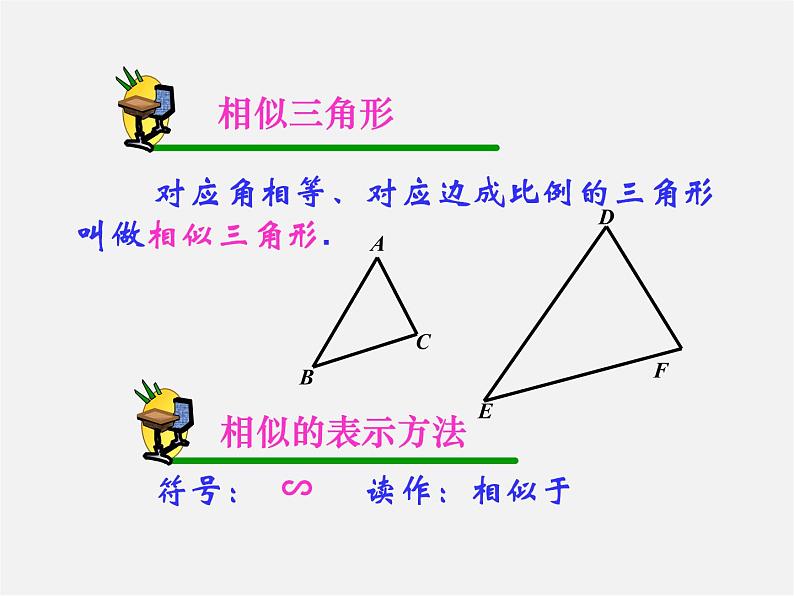
对应角相等、对应边成比例的三角形叫做相似三角形.
符号： ∽ 读作：相似于
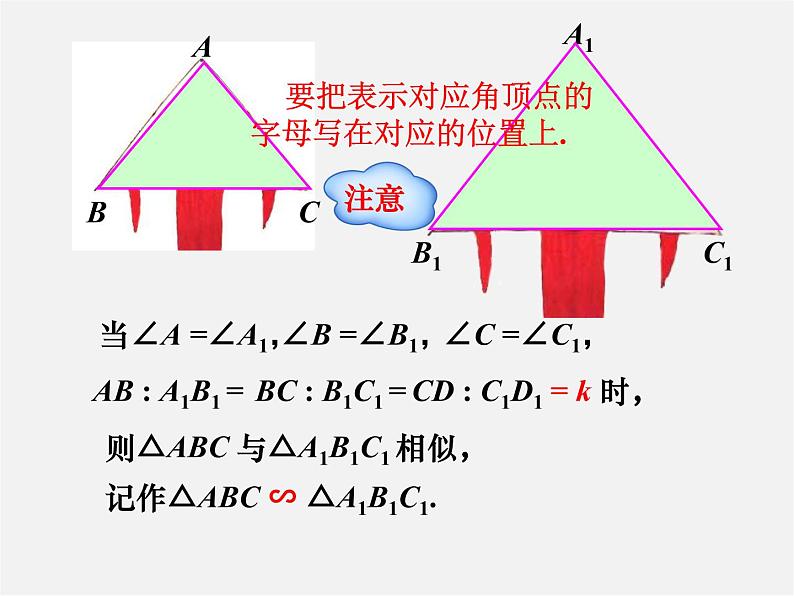
AB : A1B1 =
BC : B1C1 =
则△ABC 与△A1B1C1 相似，
记作△ABC ∽ △A1B1C1.
要把表示对应角顶点的字母写在对应的位置上.
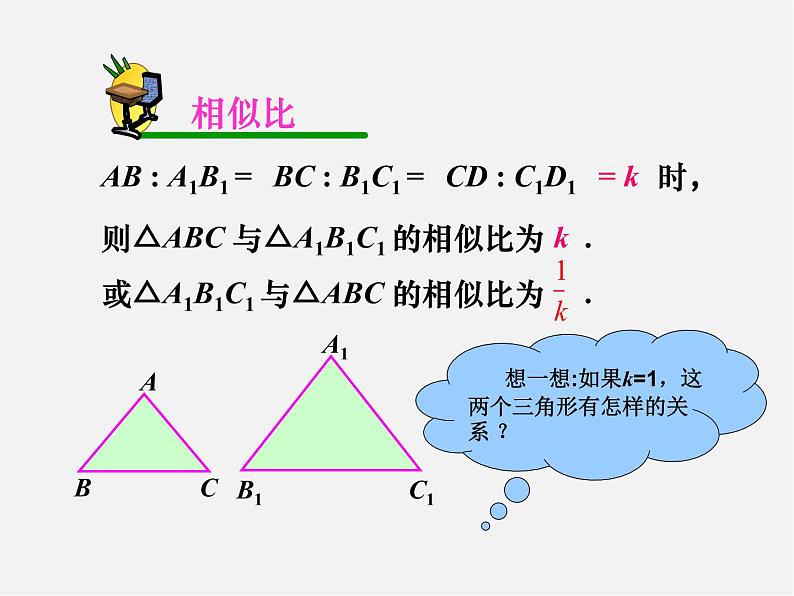
则△ABC 与△A1B1C1 的相似比为 k .或△A1B1C1 与△ABC 的相似比为 .
想一想:如果k=1，这两个三角形有怎样的关系 ？
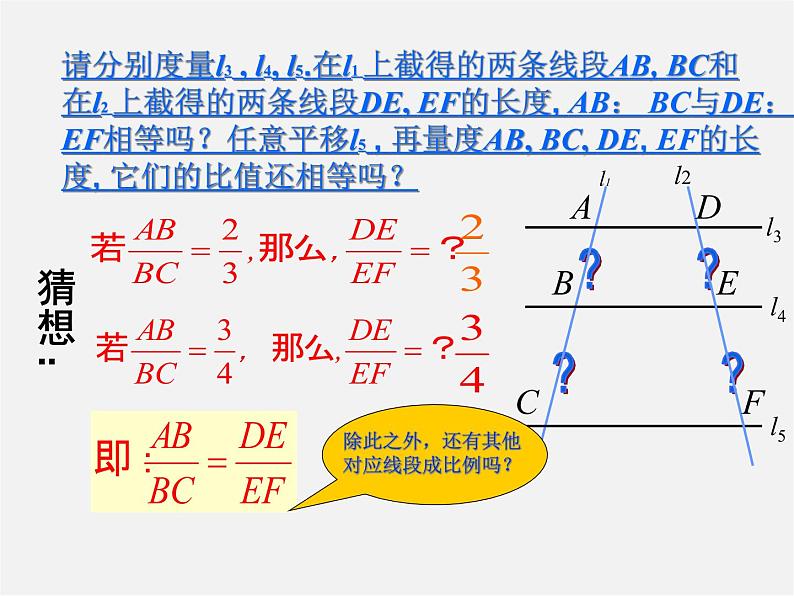
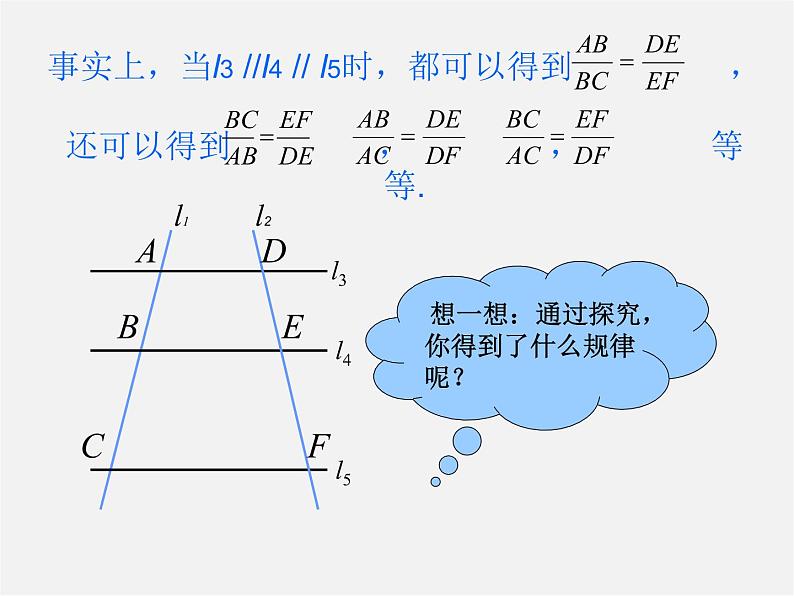
请分别度量l3 , l4, l5.在l1 上截得的两条线段AB, BC和在l2 上截得的两条线段DE, EF的长度, AB： BC与DE：EF相等吗？任意平移l5 , 再量度AB, BC, DE, EF的长度, 它们的比值还相等吗？
事实上，当l3 //l4 // l5时，都可以得到 ， 还可以得到 ， ， 等等.
想一想：通过探究，你得到了什么规律呢？
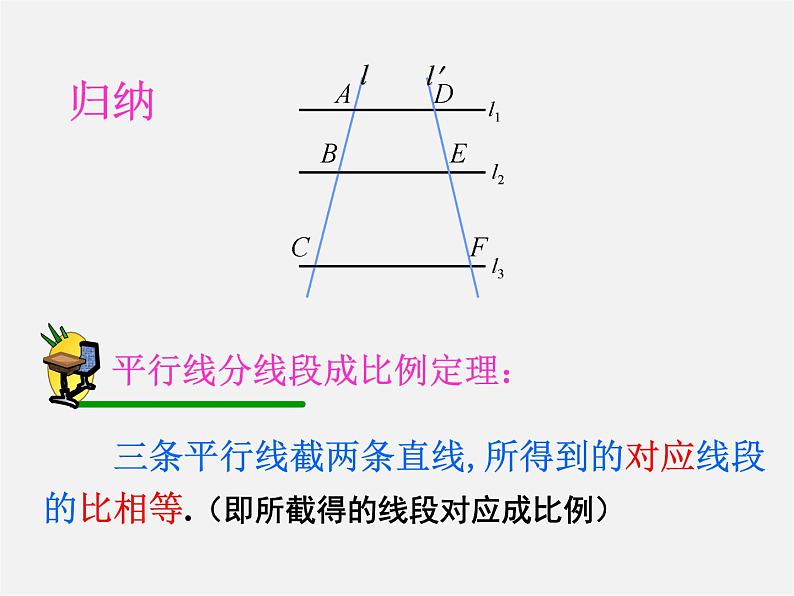
三条平行线截两条直线,所得到的对应线段的比相等.（即所截得的线段对应成比例）
平行线分线段成比例定理：
如果把图1中l1 , l2两条直线相交，交点A刚落到l3上，如图2所得的对应线段的比会相等吗？依据是什么？
如果把图1中l1 , l2两条直线相交，交点A刚落到l4上，如图2（2）所得的对应线段的比会相等吗？依据是什么？
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
例1 如图，在△ABC中，DE∥BC，AC=4 ，AB=3，EC=1.求AD和BD.
解∵AC=4，EC=1，
例2 如图所示，如果D，E，F分别在OA，OB，OC上，且DF∥AC，EF∥BC．求证：OD∶OA＝OE∶OB
证明： DF∥AC，
一、平行线分线段成比例定理： 三条平行线截两条直线，所得的对应线段成比例. （关键要能熟练地找出对应线段）
二、要熟悉该定理的几种基本图形