2022年中考复习基础必刷40题专题23直线、射线、线段

这是一份2022年中考复习基础必刷40题专题23直线、射线、线段，共32页。试卷主要包含了 下列说法错误的是， 下列说法中，错误的是等内容，欢迎下载使用。


1. 如图，AB、BC、CD、DE是四根长度均为5cm的火柴棒，点A、C、E共线．若AC=6cm，CD⊥BC，则线段CE的长度为（ ）

A.6cmB.7cmC.62cmD.8cm

2. 与三角形三个顶点距离相等的点，是这个三角形的（ ）
A.三条中线的交点B.三条角平分线的交点
C.三条高的交点D.三边的垂直平分线的交点

3. 如图，在△ABC中，DE是AC的垂直平分线，AC=6cm，且△ABD的周长为13cm，则△ABC的周长为( )cm．

A.13B.19C.10D.16

4. 点C是线段AB的中点，点D是线段AC的三等分点．若线段，则线段BD的长为（）
A.10cmB.8cmC.8cm或10cmD.2cm或4cm

5. 对于直线AB，线段CD，射线EF，在下列各图中能相交的是（ ）
A. B. C. D.

6. 如图，直线，相交于点，如果，那么是( )

A.B.C.D.

7. 如图，点在直线上，若，则的大小是（）

A.B.C.D.

8. 下列说法错误的是（ ）
A.两点之间线段最短
B.对顶角相等
C.为了了解生产的一批炮弹的杀伤半径，适宜采用全面调查的方式
D.“通常加热到100​∘C时，水沸腾”这个事情属于必然事件

9. 下列说法中，错误的是（ ）
A.一点确定一条直线B.3是无理数
C.2的相反数是−2D.30∘的余角是60∘

10. 在四边形ABCD中，对角线AC是BD的垂直平分线，∠ADB＝30∘，∠CDB＝45∘，且AB=23，则四边形ABCD的面积是（ ）
A.9+33B.18+63C.3+93D.33+922

11. 下面给出的四条线段中，最长的是（ ）

A.aB.bC.cD.d

12. 下列说法正确的是（ ）
A.延长射线AB
B.三角形的一个外角大于任何一个内角
C.圆的内接四边形的两内角互补
D.在同一平面内，两条直线不平行，它们一定相交

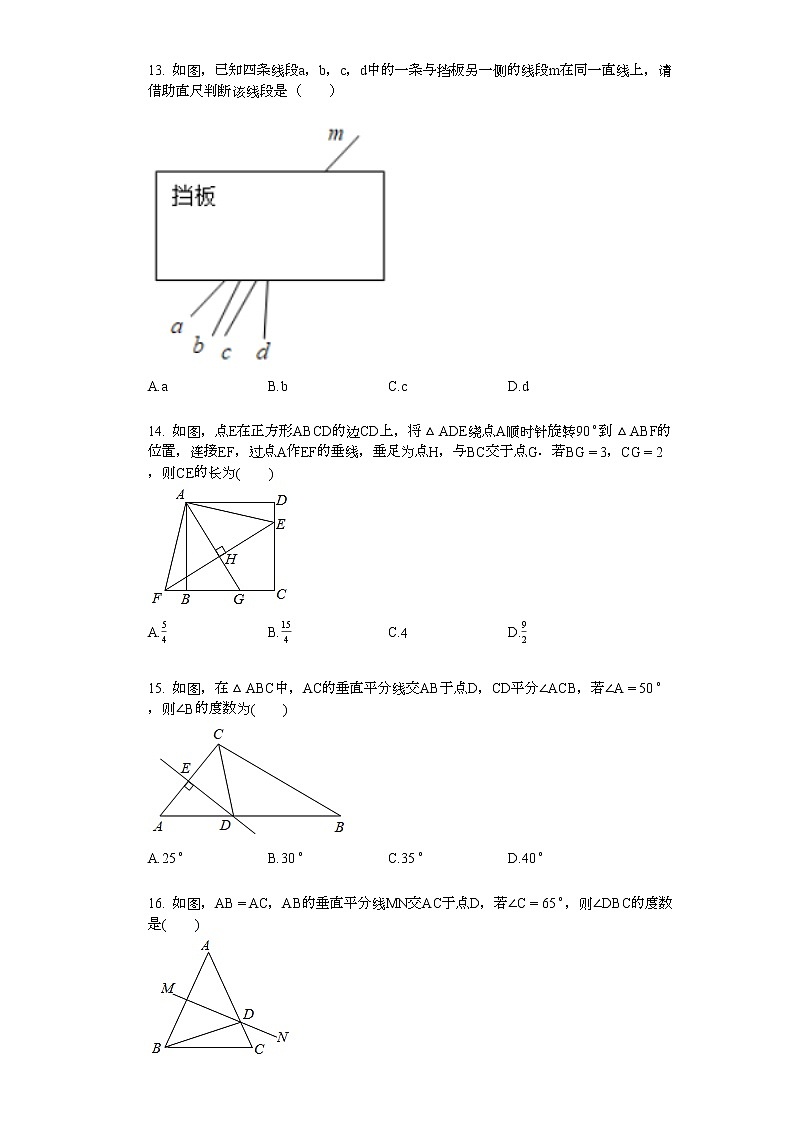
13. 如图，已知四条线段a，b，c，d中的一条与挡板另一侧的线段m在同一直线上，请借助直尺判断该线段是（ ）

A.aB.bC.cD.d

14. 如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90∘到△ABF的位置，连接EF，过点A作EF的垂线，垂足为点H，与BC交于点G．若BG=3，CG=2，则CE的长为( )

A.54B.154C.4D.92

15. 如图，在△ABC中，AC的垂直平分线交AB于点D，CD平分∠ACB，若∠A=50∘，则∠B的度数为( )

A.25∘B.30∘C.35∘D.40∘

16. 如图，AB=AC，AB的垂直平分线MN交AC于点D，若∠C=65∘，则∠DBC的度数是( )

A.25∘B.20∘C.30∘D.15∘

17. 如图，点E，F，G，Q，H在一条直线上，且EF=GH，我们知道按如图所作的直线l为线段FG的垂直平分线．下列说法正确的是（ ）

A.l是线段EH的垂直平分线
B.l是线段EQ的垂直平分线
C.l是线段FH的垂直平分线
D.EH是l的垂直平分线

18. 四边形ABCD中，E，F，G，H分别是AB，BC，CD，AD的中点，若EH=5，则FG的长度是（ ）
A.2.5B.5C.6D.10

19. 如图，在△ABC中，BC的垂直平分线分别交BC、AB于点E、F．若△AFC是等边三角形，则∠B=________​∘．


20. 如图，从甲地到乙地有四条道路，其中最短的路线是________，最长的路线是________．


21. 如图，线段的长度大约是________厘米（精确到0.1厘米）．


22. 如图，等腰△ABC中，AB=AC，AD平分∠BAC，点E是线段BC延长线上一点，连接AE，点C在AE的垂直平分线上，若DE=10cm，则AB+BD=________cm．

23. 如图，在菱形ABCD中，边AB的垂直平分线与对角线AC相交于点E，∠ABC=140∘，那么∠EDC=________．

24. 如图，在△ABC中，AC＝BC，∠B＝70∘，分别以点A，C为圆心，大于AC的长为半径作弧，两弧相交于点M，N，作直线MN，分别交AC，BC于点D，E，连接AE，则∠AED的度数是________​∘.

25. 在连接两点的所有线中，最短的是________．

26. 如图，已知边长为2的等边三角形ABC中，分别以点A，C为圆心，m为半径作弧，两弧交于点D，连结BD．若BD的长为23，则m的值为________．


27. 我们知道，两点之间线段最短，因此，连接两点间线段的长度叫做两点间的距离；同理，连接直线外一点与直线上各点的所有线段中，垂线段最短，因此，直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．类似地，连接曲线外一点与曲线上各点的所有线段中，最短线段的长度，叫做点到曲线的距离．依此定义，如图，在平面直角坐标系中，点A(2, 1)到以原点为圆心，以1为半径的圆的距离为________．


28. 如图，在Rt△ABC中，∠ACB=90∘，AC=2BC，分别以点A和B为圆心，以大于12AB的长为半径作弧，两弧相交于点M和N，作直线MN，交AC于点E，连接BE，若CE=3，则BE的长为________．


29. 在⊙O中，若弦BC垂直平分半径OA，则弦BC所对的圆周角等于________​∘．

30. 如图，菱形ABCD的边长为4，∠A=45∘，分别以点A和点B为圆心，大于12AB的长为半径作弧，两弧相交于M，N两点，直线MN交AD于点E，连接CE，则CE的长为________．


31. 如图，等腰△ABC的底边BC=20，面积为120，点D在BC边上，且CD=5，直线EF是腰AC的垂直平分线，若点M在EF上运动，则△CDM周长的最小值为________．


32. 如图，在菱形ABCD中，∠A=30∘，取大于12AB的长为半径，分别以点A，B为圆心作弧相交于两点，过此两点的直线交AD边于点E（作图痕迹如图所示），连接BE，BD．则∠EBD的度数为________．


33. 点C是线段AB的中点，点D是线段AC的三等分点．若线段AB=12cm，则线段BD的长为________cm.

34. 如图，若D是AB中点，E是BC中点，若AC=8，EC=3，AD=________.


35. 已知：△ABC，求作：△ABC的外接圆．作法：①分别作线段BC，AC的垂直平分线EF和MN，它们相交于点O；②以点O为圆心，OB的长为半径画圆．如图，⊙O即为所求，以上作图用到的数学依据有：________．（只需写一条）


36. 如图，圆O中两条互相垂直的弦AB，CD交于点E．

(1)M是CD的中点，OM=3，CD=12，求圆O的半径长；

(2)点F在CD上，且CE=EF，求证：AF⊥BD．

37. 如图，一次函数y=−x+1的图象与两坐标轴分别交于A，B两点，与反比例函数的图象交于点C(−2, m)．

(1)求反比例函数的解析式；

(2)若点P在y轴正半轴上，且与点B，C构成以BC为腰的等腰三角形，请直接写出所有符合条件的P点坐标．

38. 如图，在矩形ABCD中，对角线AC的垂直平分线分别与边AB和边CD的延长线交于点M，N，与边AD交于点E，垂足为点O．

1求证：△AOM≅△CON；

2若AB=3，AD=6，请直接写出AE的长为________．

39. 如图，已知△ABC是锐角三角形(AC
(1)请在图1中用无刻度的直尺和圆规作图：作直线l，使l上的各点到B、C两点的距离相等；设直线l与AB、BC分别交于点M、N，作一个圆，使得圆心O在线段MN上，且与边AB、BC相切；（不写作法，保留作图痕迹）

(2)在(1)的条件下，若BM=53，BC=2，则⊙O的半径为________．

40.
(1)已知如图，点C在线段AB上，线段AC=10，BC=6，点M，N分别是AC，BC的中点，求MN的长度；

(2)根据(1)的计算过程与结果，设AC+BC=a，其它条件不变，你能猜想出MN的长度吗？请用一句简洁的语言表达你发现的规律；

(3)若把(1)中的“点C在线段AB上”改为“点C在直线AB上”，结论又如何？请说明理由．
参考答案与试题解析
2022年中考复习基础必刷题40题——专题二十二_直线、射线、线段
一、 选择题 （本题共计 18 小题 ，每题 3 分 ，共计54分 ）
1.
【答案】
D
【考点】
线段的和差
比较线段的长短
两点间的距离
【解析】
此题暂无解析
【解答】
解：分别过B、D作AE的垂线，垂足分别为F、G，
∵ CD⊥BC，
∴ ∠BCF+∠FBC=90∘,∠BCF+∠GCD=90∘，
∴ ∠FBC=∠GCD，
在△BFC和△CGD中；
∠BFC=∠CGD∠FBC=∠GCDBC=CD，
∴ △BFC≅△CGD
∴ BF=CG，
∵ AB=BC=CD=DE=5cm，
∴ △ABC,△CDE均为等腰三角形，
∵ AC=6cm，
∴ FC=12AC=3cm，
∴ BF=BC2−FC2=52−32=4cm，
∴ CE=2CG=2BF=2×4=8cm
故选D．
2.
【答案】
D
【考点】
线段垂直平分线的性质
【解析】
可分别根据线段垂直平分线的性质进行思考，首先满足到A点、B点的距离相等，然后思考满足到C点、B点的距离相等，都分别在各自线段的垂直平分线上，于是答案可得．
【解答】
解：如图：
∵ OA=OB，∴ O在线段AB的垂直平分线上，
∵ OB=OC，∴ O在线段BC的垂直平分线上，
∵ OA=OC，∴ O在线段AC的垂直平分线上，
又相交于一点，
∴ 与三角形三个顶点距离相等的点，是这个三角形的三边的垂直平分线的交点．
故选D.
3.
【答案】
B
【考点】
线段垂直平分线的性质
【解析】
根据线段垂直平分线得出AD＝DC，求出三角形ABD周长＝AB+BC＝13cm，即可求出答案．
【解答】
解：∵ DE是AC的垂直平分线，
∴ AD=DC，
∵ △ABD的周长为13cm，
∴ AB+BD+AD=AB+BD+DC=AB+BC=13(cm)，
∵ AC=6cm，
∴ △ABC的周长为AB+BC+AC=13+6=19(cm).
故选B.
4.
【答案】
C
【考点】
线段的中点
线段的和差
两点间的距离
【解析】
根据题意作图，由线段之间的关系即可求解．
【解答】
如图，点C是线段AB的中点，
．AC=BC=12AB=6cm
当AD=23AC=4cm时，CD=AC−AD=2cm
…BD=BC+CD=6+2=8cm
当|AD=13AC=2cm时，CD=ACAD=4cm
∴ BD=BC+CD=6+4=10cm;
故选C．
Ae→B
D1D2C
5.
【答案】
B
【考点】
直线、射线、线段
余角和补角
全等三角形的判定
【解析】
根据直线能向两方无限延伸，射线能向一方无限延伸，线段不能延伸，据此进行选择．
【解答】
B中这条直线与这条射线能相交；A中直线和线段不能相交；C中射线和线段不能相交；D中直线和射线不能相交．
6.
【答案】
A
【考点】
直线、射线、线段
对顶角
余角和补角
【解析】
根据对顶角相等求出−1，再根据互为邻补角的两个角的和等于180∘列式计算即可得解．
【解答】
解：∠1+∠2=60∘,∠1=22（对顶角相等），
∠1=30∘
∠1与∠3互为邻补角，
∴ 2=180∘−∠1=180∘−30∘=150∘
故选：A．
7.
【答案】
C
【考点】
直线、射线、线段
三角形的外角性质
余角和补角
【解析】
试题分析：根据点O在直线AB上，∠BOC=60∘，即可得出∠AOC的度数．点O在直线AB上，∴ ∠AOB=180∘
又∠BOC=60∘△AOC=120∘，故选C．
【解答】
此题暂无解答
8.
【答案】
C
【考点】
随机事件
线段的性质：两点之间线段最短
对顶角
全面调查与抽样调查
【解析】
根据线段的公理，对顶角的性质，抽样调查的事件的特点，必然事件的定义求解．
【解答】
解：A、两点之间线段最短，正确，故选项错误；
B、对顶角相等，正确，故选项错误；
C、了解生产的一批炮弹的杀伤半径，调查过程带有破坏性，只能采取抽样调查，而不能将整批炮弹全部用于实验，错误，故选项正确；
D、“通常加热到100​∘C时，水沸腾”这个事情属于必然事件，正确，故选项错误．
故选C．
9.
【答案】
A
【考点】
无理数的判定
相反数
直线的性质：两点确定一条直线
余角和补角
【解析】
过一点可以作无数条直线，3是无理数，2的相反数是−2，30∘的余角是60∘，根据以上内容判断即可．
【解答】
解：A、过一点可以作无数条直线，错误，故本选项正确；
B、3是无理数，正确，故本选项错误；
C、2的相反数是−2，正确，故本选项错误；
D、30∘的余角是60∘，正确，故本选项错误；
故选A．
10.
【答案】
A
【考点】
线段垂直平分线的性质
勾股定理
【解析】
认真观察图形，四边形ABCD的面积＝S△ABD+S△BCD．根据题意易求BD，OA，OC．
【解答】
∵ 对角线AC是BD的垂直平分线，∴ AD＝AB＝23．
在△AOD中，∠ADB＝30∘，∠AOD＝90∘，
∴ OA=12AD=3．
∴ OD＝3，BD＝6．
在△COD中，∠CDB＝45∘，∠COD＝90∘，
∴ OC＝OD＝3．
∴ 四边形ABCD的面积＝S△ABD+S△BCD=12BD⋅OA+12BD⋅OC＝9+33．
11.
【答案】
D
【考点】
比较线段的长短
【解析】
本题可通过观察、比较图形直接得出结果．
【解答】
解：通过观察比较：d线段长度最长．
故选D．
12.
【答案】
D
【考点】
圆内接四边形的性质
直线、射线、线段
平行线的概念及表示
三角形的外角性质
【解析】
根据射线的性质判断A；
根据三角形外角的性质判断B；
根据圆内接四边形的性质判断C；
根据在同一平面内，两条直线的位置关系判断D．
【解答】
解：A、射线有一个延伸方向，射线AB的端点是A，由A向B是无限延伸的，只能说反向延长射线AB，故本选项错误；
B、三角形的一个外角大于和它不相邻的任何一个内角，故本选项错误；
C、圆内接四边形的对角互补，故本选项错误；
D、在同一平面内，两条直线的位置关系只有两种：平行或相交，所以在同一平面内，两条直线不平行，它们一定相交，故本选项正确．
故选D．
13.
【答案】
A
【考点】
直线的性质：两点确定一条直线
【解析】
此题暂无解析
【解答】
解：设线段m与挡板的交点为A，a、b、c、d与挡板的交点分别为B，C，D，E，连结AB、AC、AD、AE，根据直线的特征经过两点有且只有一条直线，利用直尺可确定线段a与m在同一直线上，
故选A．
14.
【答案】
B
【考点】
勾股定理
正方形的性质
旋转的性质
线段垂直平分线的性质
【解析】
连接EG，根据AG垂直平分EF，即可得出EG＝FG，设CE＝x，则DE＝5−x＝BF，FG＝EG＝8−x，再根据Rt△CEG中，CE2+CG2＝EG2，即可得到CE的长．
【解答】
解：如图所示，连接EG，
由旋转可得，△ADE≅△ABF，
∴ AE=AF，DE=BF，
又∵ AG⊥EF，
∴ H为EF的中点，
∴ AG垂直平分EF，
∴ EG=FG，
设CE=x，则DE=5−x=BF，FG=8−x，
∴ EG=8−x，
∵ ∠C=90∘，
∴ Rt△CEG中，CE2+CG2=EG2，即x2+22=(8−x)2，
解得x=154，
∴ CE的长为154.
故选B.
15.
【答案】
B
【考点】
三角形内角和定理
线段垂直平分线的性质
【解析】
依据线段垂直平分线的性质，即可得到∠A＝∠ACD，再根据角平分线的定义，即可得出∠ACB的度数，根据三角形内角和定理，即可得到∠B的度数．
【解答】
解：∵ DE垂直平分AC，
∴ AD=CD，
∴ ∠A=∠ACD，
又∵ CD平分∠ACB，
∴ ∠ACB=2∠ACD=100∘，
∴ ∠B=180∘−∠A−∠ACB=180∘−50∘−100∘=30∘.
故选B.
16.
【答案】
D
【考点】
等腰三角形的性质
线段垂直平分线的性质
【解析】
根据等腰三角形的性质得到∠ABC，再根据垂直平分线的性质求出∠ABD，从而可得结果．
【解答】
解：∵AB=AC，
∴∠C=∠ABC=65∘，
∴∠A=180∘−65∘×2=50∘.
∵MN垂直平分AB，
∴AD=BD，
∴∠A=∠ABD=50∘，
∴∠DBC=∠ABC−∠ABD=15∘.
故选D.
17.
【答案】
A
【考点】
线段垂直平分线的性质
【解析】
根据垂直平分线的性质定理判断即可．
【解答】
解：如图.
A．∵ 直线l为线段FG的垂直平分线，
∴ FO=GO，l⊥FG.
∵ EF=GH，
∴ EF+FO=OG+GH，即EO=OH，
∴ l为线段EH的垂直平分线，故此选项正确；
B．∵ EO≠OQ，
∴ l不是线段EQ的垂直平分线，故此选项错误；
C．∵ FO≠OH，
∴ l不是线段FH的垂直平分线，故此选项错误；
D．∵ l为直线，EH不能平分直线l，
∴ EH不是l的垂直平分线，故此选项错误.
故选A.
18.
【答案】
B
【考点】
两点间的距离
【解析】
E、F、G、H分别是AB、BC、CD、AD的中点，可得EH、FG分别为△ABD、△BCD的中位线，根据中位线定理，EH=FG=12BD=5．
【解答】
解：∵ 四边形ABCD中，E、F、G、H分别是AB、BC、CD、AD的中点，EH=5，
∴ EH，FG分别是△ABD与△BCD的中位线，
∴ EH=FG=12BD=5．
故选：B．
二、 填空题 （本题共计 17 小题 ，每题 3 分 ，共计51分 ）
19.
【答案】
30
【考点】
等边三角形的性质
线段垂直平分线的性质
三角形的外角性质
【解析】
根据垂直平分线的性质得到∠B＝∠BCF，再利用等边三角形的性质得到∠AFC＝60∘，从而可得∠B的度数．
【解答】
解：∵ EF垂直平分BC，
∴ BF=CF，
∴ ∠B=∠BCF，
∵ △AFC是等边三角形，
∴ ∠AFC=60∘，
∴ ∠B=∠BCF=12∠AFC=30∘．
故答案为：30．
20.
【答案】
从甲经A到乙,从甲经D到乙
【考点】
线段的性质：两点之间线段最短
【解析】
考查最短，最长路径问题，结合图形，即可求解．
【解答】
解：由图可得，因为两点之间，线段最短，所以最短的路线为从甲经A到乙，而最长路线则为从甲经D到乙．
故答案为：从甲经A到乙；从甲经D到乙．
21.
【答案】
2.3（或2.4）
【考点】
比较线段的长短
【解析】
根据对线段长度的估算，可得答案．
【解答】
解：线段的长度大约是2.3（或2.4）厘米，
故答案为：2.3（或2.4）．
22.
【答案】
10
【考点】
线段垂直平分线的性质
等腰三角形的判定与性质
【解析】
根据线段垂直平分线上的点到线段两端点的距离相等可得AC=CE，根据等腰三角形三线合一的性质可得BD=CD，然后求出AD+BD=DE．
【解答】
解：∵ 点C在AE的垂直平分线上，
∴ AC=CE，
∵ AB=AC，AD平分∠BAC，
∴ BD=CD，
∴ AB+BD=AC+CD=CE+CD=DE，
∵ DE=10cm，
∴ AB+BD=10cm．
故答案为：10．
23.
【答案】
120∘
【考点】
菱形的性质
线段垂直平分线的性质
【解析】
连结BE，根据菱形的轴对称性得∠EDC=∠EBC，再根据等腰三角形的性质和三角形的内角和定理，求得∠EBC的度数，问题即可得到解决．
【解答】
解：连结BE，
∵ 四边形ABCD是菱形，
∴ AB=CB，
∵ ∠ABC=140∘，
∴ ∠BAC=∠BCA=20∘．
又∵ 有一条直线垂直平分AB，
∴ EA=EB，
∴ ∠BAE=∠EBA=20∘，
∴ ∠EBC=∠ABC−∠ABE=140∘−20∘=120∘，
又∵ △BEC与△CDE关于AC对称，
∴ ∠EDC=∠EBC=120∘．
故答案为：120∘．
24.
【答案】
50
【考点】
线段垂直平分线的性质
线段的垂直平分线的性质定理的逆定理
【解析】
试题分析：．由作图可知，MN是线段AC的垂直平分线，CE=AE
∠C=2CAE
AC=BC,∠B=70∘
ΔC=40∘
∠AED=50∘
故答案为50．
【解答】
此题暂无解答
25.
【答案】
线段
【考点】
线段的性质：两点之间线段最短
【解析】
根据线段的性质，两点之间线段最短可得出答案．
【解答】
解：在连接两点的所有线中，最短的是线段．
故填：线段．
26.
【答案】
2或27
【考点】
作线段的垂直平分线
勾股定理
等边三角形的性质
线段垂直平分线的性质
【解析】
由作图知，点D在AC的垂直平分线上，得到点B在AC的垂直平分线上，求得BD垂直平分AC，设垂足为E，得到BE=3，当点D、B在AC的两侧时，如图，当点D、B在AC的同侧时，如图，解直角三角形即可得到结论．
【解答】
解：由作图知，点D在AC的垂直平分线上，
∵ △ABC是等边三角形，
∴ 点B在AC的垂直平分线上，
∴ BD垂直平分AC，
设垂足为E，
∵ AC=AB=2，
∴ BE=3，
当点D、B在AC的两侧时，
∵ BD=23，
∴ BE=DE，
∴ AD=AB=2，
∴ m=2；
当点D、B在AC的同侧时，
∵ BD′=23，
∴ D′E=33，
∴ AD′=(33)2+12=27，
∴ m=27，
综上所述，m的值为2或27.
故答案为：2或27.
27.
【答案】
5−1
【考点】
垂线段最短
线段的性质：两点之间线段最短
勾股定理
距离问题
【解析】
连接AO交⊙O于B，则线段AB的长度即为点A(2, 1)到以原点为圆心，以1为半径的圆的距离，根据勾股定理即可得到结论．
【解答】
解：连接AO交⊙O于B，
则线段AB的长度即为点A(2, 1)到以原点为圆心，以1为半径的圆的距离，
∵ 点A(2, 1)，
∴ OA=22+12=5，
∵ OB=1，
∴ AB=OA−OB=5−1，
即点A(2, 1)到以原点为圆心，以1为半径的圆的距离为5−1.
故答案为：5−1.
28.
【答案】
5
【考点】
作图—基本作图
线段垂直平分线的性质
勾股定理
【解析】
设BE＝AE＝x，在Rt△BEC中，利用勾股定理构建方程即可解决问题．
【解答】
解：由作图可知，MN垂直平分线段AB，
∴ AE=EB，
设AE=EB=x，
∵ EC=3，AC=2BC，
∴ BC=12(x+3)，
在Rt△BCE中，∵ BE2=BC2+EC2，
∴ x2=32+[12(x+3)]2，
解得，x=5或−3（舍弃），
∴ BE=5.
故答案为：5.
29.
【答案】
60∘或120
【考点】
圆周角定理
垂径定理
线段垂直平分线的性质
【解析】
根据弦BC垂直平分半径OA，可得OD:OB＝1:2，得∠BOC＝120∘，根据同弧所对圆周角等于圆心角的一半即可得弦BC所对的圆周角度数．
【解答】
如图，
∵ 弦BC垂直平分半径OA，
∴ OD:OB=1:2，
∴ ∠BOD=60∘，
∴ ∠BOC=120∘，
∴ 弦BC所对的圆周角等于60∘或120∘．
故答案为：60∘或120∘．
30.
【答案】
26
【考点】
菱形的性质
线段垂直平分线的性质
勾股定理
【解析】
如图，连接EB．证明△AEB是等腰直角三角形，利用勾股定理求出AE，EB，EC即可．
【解答】
解：如图，连接EB．
由作图可知，MN垂直平分线段AB，
∴ EA=EB，
∴ ∠A=∠EBA=45∘，
∴ ∠AEB=90∘.
∵ AB=4，
∴ EA=EB=22.
∵ 四边形ABCD是菱形，
∴ AD // BC，
∴ ∠EBC=∠AEB=90∘，
∴ EC=EB2+BC2=(22)2+42=26.
故答案为：26.
31.
【答案】
18
【考点】
线段垂直平分线的性质
等腰三角形的性质
轴对称——最短路线问题
【解析】
如图作AH⊥BC于H，连接AM，由EF垂直平分线段AC，推出MA＝MC，推出DM+MC＝AM+MD，可得当A、D、M共线时，DM+MC的值最小，最小值就是线段AD的长，利用勾股定理可求AD的长，即可求解．
【解答】
解：如图，作AH⊥BC于H，

连接AM，
∵ EF垂直平分线段AC，
∴ MA=MC，
DM+MC=AM+MD，
∴ 当A、D、M三点共线时， DM+MC的值最小，
∵ 等腰△ABC的底边BC=20，面积为120，AH⊥BC，
∴ BH=CH=10,AH=120×220=12，
DH=CH−CD=5,
AD=AH2+HD2=144+25=13，
DM+MC的最小值为13，
△CDM周长的最小值=13+5=18.
故答案为：18.
32.
【答案】
45∘
【考点】
线段垂直平分线的性质
菱形的性质
作线段的垂直平分线
【解析】
根据∠EBD＝∠ABD−∠ABE，求出∠ABD，∠ABE即可解决问题．
【解答】
解：∵ 四边形ABCD是菱形，
∴ AD=AB，
∴ ∠ABD=∠ADB=12(180∘−∠A)=75∘.
由作图可知，EA=EB，
∴ ∠ABE=∠A=30∘，
∴ ∠EBD=∠ABD−∠ABE=75∘−30∘=45∘.
故答案为：45∘.
33.
【答案】
10或8
【考点】
线段的和差
线段的中点
【解析】
根据线段中点的定义和线段三等分点的定义即可得到结论．
【解答】
解：∵ C是线段AB的中点，AB=12cm，
∴ AC=BC=12AB=12×12=6(cm)，
点D是线段AC的三等分点，
①当AD=13AC时，
BD=BC+CD=BC+23AC=6+4=10(cm)；
②当AD=23AC时，
BD=BC+CD=BC+13AC=6+2=8(cm)．
所以线段BD的长为10cm或8cm.
故答案为：10或8.
34.
【答案】
1
【考点】
线段的和差
线段的中点
【解析】
先根据EC=3，E是BC中点求出BC的长，再根据AC=8求出AB的长，最后根据D是AB的中点求出AD的长即可．
【解答】
解：∵ EC=3，E是BC中点，
∴ BC=2EC=2×3=6，
∵ AC=8，
∴ AB=AC−BC=8−6=2，
∵ D是AB中点，
∴ AD=12AB=12×2=1．
故答案为：1.
35.
【答案】
线段的垂直平分线的性质
【考点】
三角形的外接圆与外心
线段垂直平分线的性质
【解析】
利用线段垂直平分线的性质得到OA＝OC＝OB，然后根据点与圆的位置关系可判断点A、C在⊙O上．
【解答】
解：∵ 点O为AC和BC的垂直平分线的交点，
∴ OA=OC=OB，
∴ ⊙O为△ABC的外接圆．
故答案为：线段的垂直平分线的性质.
三、 解答题 （本题共计 5 小题 ，每题 10 分 ，共计50分 ）
36.
【答案】
(1)解：连接OC，如图，
∵ OM平分CD，
∴OM⊥CD，
∴∠OMC=90∘，
∵ CD=12，
∴MC=6，
在Rt△OMC 中，OC=MC2+OM2
=62+32
=35.
（2）∵ CE=EF, AB⊥CD，
∴ AF=AC, ∠1=∠3,
∵ ∠B=∠C ，
∴ ∠3+∠C=∠2+∠B， ∠3=∠2，
∴ ∠1=∠2，
∵ ∠1+∠B=∠2+∠B=90∘ ，
∴ AF⊥BD.
【考点】
垂径定理
勾股定理
等腰三角形的性质：三线合一
线段垂直平分线的性质
【解析】
此题暂无解析
【解答】
(1)解：连接OC，如图，
∵ OM平分CD，
∴OM⊥CD，
∴∠OMC=90∘，
∵ CD=12，
∴MC=6，
在Rt△OMC 中，OC=MC2+OM2
=62+32
=35.
（2）∵ CE=EF, AB⊥CD，
∴ AF=AC, ∠1=∠3,
∵ ∠B=∠C ，
∴ ∠3+∠C=∠2+∠B， ∠3=∠2，
∴ ∠1=∠2，
∵ ∠1+∠B=∠2+∠B=90∘ ，
∴ AF⊥BD.
37.
【答案】
解：(1)点C−2,m在一次函数y=−x+1的图象上，
把C点坐标代入y=−x+1得m=−−2+1=3，
∴ 点C的坐标是−2,3，
设反比例函数的解析式为y=kxk≠0，
把点C的坐标−2,3代入y=kx得， 3=k−2，
解得k=−6，
∴ 反比例函数的解析式为y=−6x.
(2)在直线y=−x+1中，令x=0，则y=1，
∴ B0,1，
∴BC=3−12+−22=22，
当BC=BP时，BP=22，
OP=22+1，
P0,22+1，
当BC=PC时，点C在BP的垂直平分线上，
此时P0,5
即满足条件的点P的坐标为0,5或0,22+1.
【考点】
反比例函数图象上点的坐标特征
反比例函数与一次函数的综合
等腰三角形的性质
线段垂直平分线的性质
【解析】
（1）先确定出点C坐标，再代入反比例函数解析式中，即可得出结论；
（2）分两种情况，利用等腰三角形的性质，即可得出结论．
【解答】
解：(1)点C−2,m在一次函数y=−x+1的图象上，
把C点坐标代入y=−x+1得m=−−2+1=3，
∴ 点C的坐标是−2,3，
设反比例函数的解析式为y=kxk≠0，
把点C的坐标−2,3代入y=kx得， 3=k−2，
解得k=−6，
∴ 反比例函数的解析式为y=−6x.
(2)在直线y=−x+1中，令x=0，则y=1，
∴ B0,1，
∴BC=3−12+−22=22，
当BC=BP时，BP=22，
OP=22+1，
P0,22+1，
当BC=PC时，点C在BP的垂直平分线上，
此时P0,5
即满足条件的点P的坐标为0,5或0,22+1.
38.
【答案】
(1)证明：∵ MN是AC的垂直平分线，
∴ AO=CO，∠AOM=∠CON=90∘，
∵ 四边形ABCD是矩形，
∴ AB // CD，
∴ ∠M=∠N，
在△AOM和△CON中，
∠M=∠N，∠AOM=∠CON，AO=CO，
∴ △AOM≅△CON(AAS).
154
【考点】
矩形的性质
线段垂直平分线的性质
全等三角形的判定
勾股定理
【解析】
1利用线段垂直平分线的性质以及矩形的性质，即可得到判定△AOM≅△CON的条件；
2连接CE，设AE=CE=x，则DE=6−x，再根据勾股定理进行计算，即可得到AE的长．
【解答】
(1)证明：∵ MN是AC的垂直平分线，
∴ AO=CO，∠AOM=∠CON=90∘，
∵ 四边形ABCD是矩形，
∴ AB // CD，
∴ ∠M=∠N，
在△AOM和△CON中，
∠M=∠N，∠AOM=∠CON，AO=CO，
∴ △AOM≅△CON(AAS).
2解：如图所示，连接CE，
∵ MN是AC的垂直平分线，
∴ CE=AE，
设AE=CE=x，则DE=6−x，
∵ 四边形ABCD是矩形，
∴ ∠CDE=90∘，CD=AB=3，
∴ Rt△CDE中，CD2+DE2=CE2，
即32+(6−x)2=x2，
解得x=154，
即AE的长为154．
故答案为：154．
39.
【答案】
解：(1)如图直线l，⊙O即为所求．
12
【考点】
角平分线的性质
作线段的垂直平分线
线段垂直平分线的性质
三角形的面积
【解析】
（1）作线段BC的垂直平分线交AB于M，交BC于N，作∠ABC的角平分线交MN于点O，以O为圆心，ON为半径作⊙O即可．
（2）过点O作OE⊥AB于E．设OE＝ON＝r，利用面积法构建方程求解即可．
【解答】
解：(1)如图直线l，⊙O即为所求．
(2)过点O作OE⊥AB于E．设OE=ON=r，
∵ BM=53，BC=2，MN垂直平分线段BC，
∴ BN=CN=1，
∴ MN=BM2−BN2=(53)2−11=43，
∵ s△BNM=S△BNO+S△BOM，
∴ 12×1×43=12×1×r+12×53×r，
解得，r=12．
故答案为：12．
40.
【答案】
解：(1)∵ 点M，N分别是AC，BC的中点，
∴ CM=12AC=5，CN=12BC=3，
∴ MN=CM+CN=5+3=8.
(2)MN的长度为：12a．
∵ 同(1)可得CM=12AC，CN=12BC，
∴ MN=CM+CN=12AC+12BC
=12(AC+BC)=12a，
即MN的长度就等于AC与BC长度和的一半.
(3)①当点C在线段AB上时，则MN=12AC+12BC=8；
②当点C在线段AB的延长线上时，如图，
则MN=12AC−12BC=5−3=2．
【考点】
线段的中点
线段的和差
【解析】
（1）根据“点M、N分别是AC、BC的中点”，先求出MC、CN的长度，再利用MN=CM+CN即可求出MN的长度；
（2）与（1）同理，先用AC、BC表示出MC、CN，MN的长度就等于AC与BC长度和的一半；
（3）本题应考虑到A、B、C三点之间的位置关系的多种可能，即当点C在线段AB上时和当点C在线段AB的延长线上时．
【解答】
解：(1)∵ 点M，N分别是AC，BC的中点，
∴ CM=12AC=5，CN=12BC=3，
∴ MN=CM+CN=5+3=8.
(2)MN的长度为：12a．
∵ 同(1)可得CM=12AC，CN=12BC，
∴ MN=CM+CN=12AC+12BC
=12(AC+BC)=12a，
即MN的长度就等于AC与BC长度和的一半.
(3)①当点C在线段AB上时，则MN=12AC+12BC=8；
②当点C在线段AB的延长线上时，如图，
则MN=12AC−12BC=5−3=2．