初中数学3.5 三角形的内切圆备课ppt课件

这是一份初中数学3.5 三角形的内切圆备课ppt课件，共11页。PPT课件主要包含了导入新课，☉O就是所求的圆，讲授新课，填一填，例题讲解，解得x4，∴OB＝BC＝3等内容，欢迎下载使用。

问题 一张三角形的铁皮，如何在它上面截下一块圆形的用料，使截出的圆与三角形各边都相切呢？
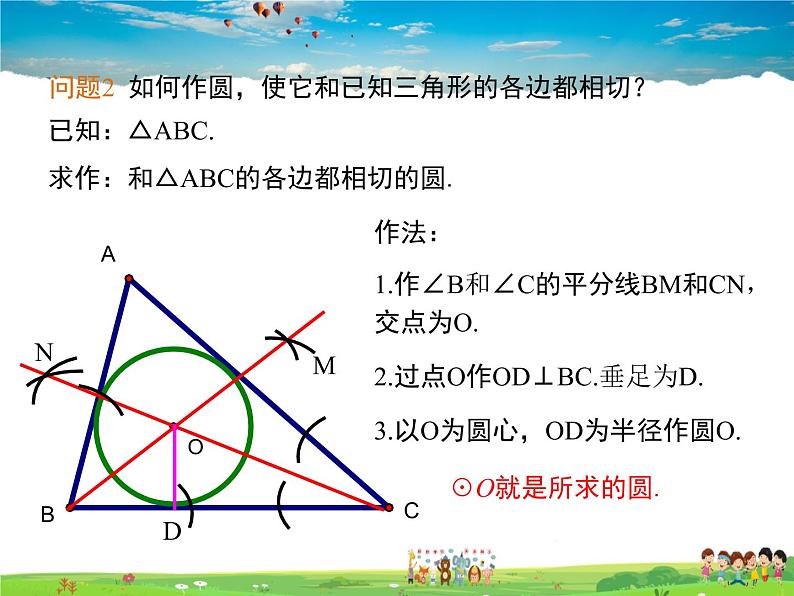
问题2 如何作圆，使它和已知三角形的各边都相切？
已知：△ABC.求作：和△ABC的各边都相切的圆.
作法：1.作∠B和∠C的平分线BM和CN，交点为O.2.过点O作OD⊥BC.垂足为D.3.以O为圆心，OD为半径作圆O.
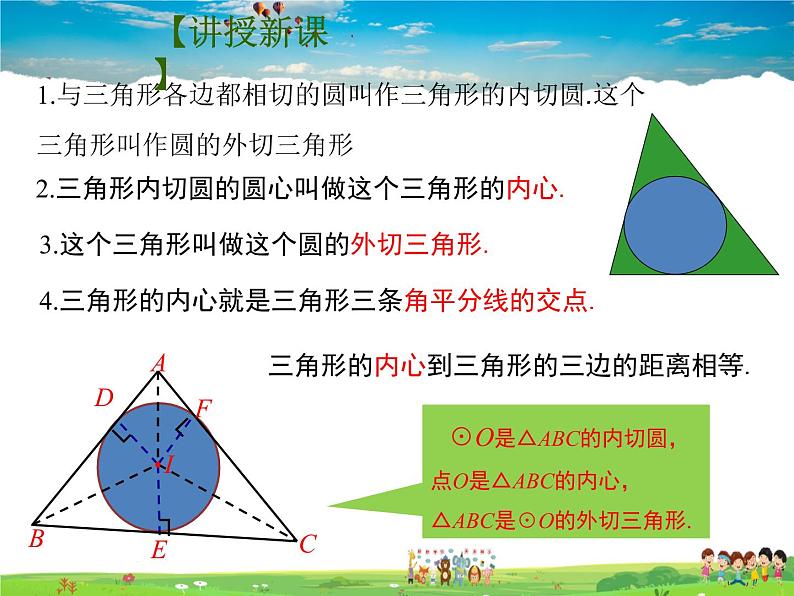
1.与三角形各边都相切的圆叫作三角形的内切圆.这个三角形叫作圆的外切三角形
2.三角形内切圆的圆心叫做这个三角形的内心.
3.这个三角形叫做这个圆的外切三角形.
4.三角形的内心就是三角形三条角平分线的交点.
三角形的内心到三角形的三边的距离相等.
☉O是△ABC的内切圆，点O是△ABC的内心，△ABC是☉O的外切三角形.
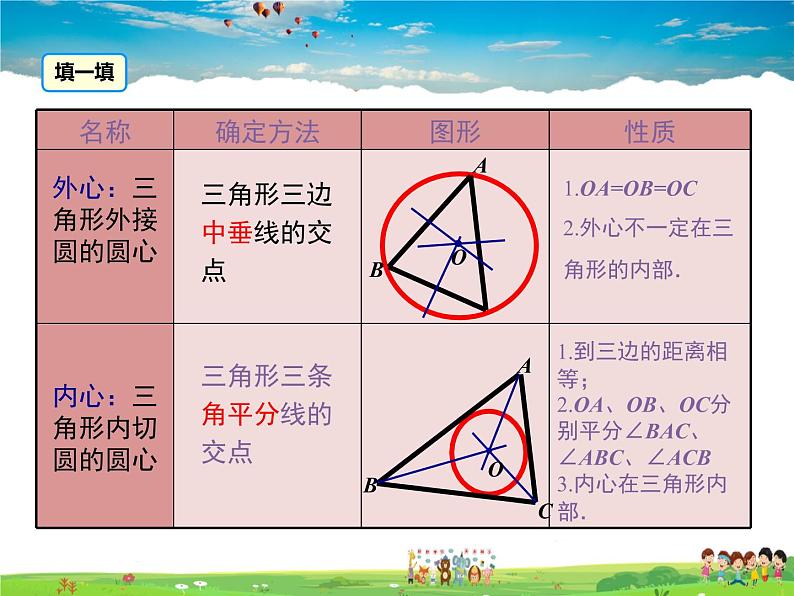
三角形三边中垂线的交点
1.OA=OB=OC2.外心不一定在三角形的内部．
三角形三条角平分线的交点
1.到三边的距离相等；2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB3.内心在三角形内部．
例1 △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F，且AB=13cm，BC=14cm，CA=9cm，求AF、BD、CE的长.
想一想：图中你能找出哪些相等的线段？理由是什么？
设AF=xcm，则AE=xcm.
∴CE=CD=AC-AE=9-x(cm)， BF=BD=AB-AF=13-x(cm).
由 BD+CD=BC，可得 (13-x)+(9-x)=14，
∴ AF=4(cm)，BD=9(cm)，CE=5(cm).
方法小结：关键是熟练运用切线长定理，将相等线段转化集中到某条边上，从而建立方程.
△ABC的内切圆☉O与三边分别切于D、E、F三点，如图，已知AF=3,BD+CE=12,则△ABC的周长是 .
直角三角形的两直角边分别是3cm ,4cm,试问：（1）它的外接圆半径是 cm;内切圆半径是 cm？（2）若移动点O的位置，使☉O保持与△ABC的边AC、BC都相切，求☉O的半径r的取值范围.
解：如图所示，设与BC、AC相切的最大圆与BC、AC的切点分别为B、D,连接OB、OD,则四边形BODC为正方形.
∴半径r的取值范围为0＜r≤3.