专题07函数的图像、函数与方程 （文理通用）常考点归纳与变式演练（学生版）学案

专题08  函数的图像、函数与方程

专题导航

常考点归纳

常考点01 函数图像的识辨

【典例1】

1．(2019年高考数学课标Ⅲ卷理科)函数在的图像大致为 (　　)

A． B．

C． D．

2．如图，长方形的边，，是的中点，点沿着边，与运动，记．将动到、两点距离之和表示为的函数，则的图像大致为              (　　)

 (　　)

【考点总结与提高】

寻找函数图像与解析式之间的6种对应关系

①从函数的定义域，判断图像的左右位置，

②从函数的值域(或有界性)，判断图像的上下位置；

③从函数的单调性，判断图像的升降变化趋势；

④从函数的奇偶性，判断图像的对称性：

奇函数的图像关于原点对称，在对称的区间上单调性一致，

偶函数的图像关于y轴对称，在对称的区间上单调性相反；

⑤从函数的周期性，判断图像是否具有循环往复特点；

⑥从特殊点出发，排除不符合要求的选项，如f(0)的值，当x>0时f(x)的正负等．

【变式演练1】

1．函数的图象大致为 (　　)

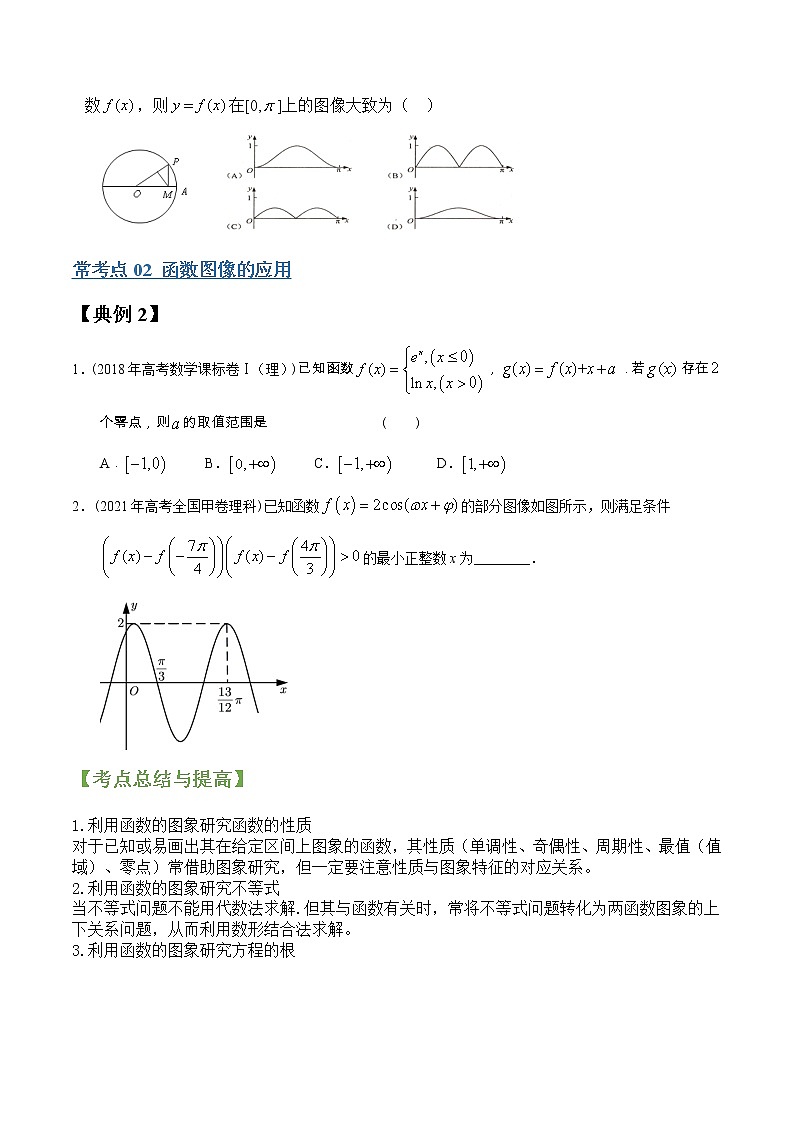
2．如图，圆O的半径为1，A是圆上的定点，P是 圆上的动点，角的始边为射线，终边为射线，过点作直线的垂线，垂足为，将点到直线的距离表示为的函数，则=在[0,]上的图像大致为（  ）

常考点02 函数图像的应用

【典例2】

1．(2018年高考数学课标卷Ⅰ（理）)已知函数，．若存在个零点，则的取值范围是 (　　)

A．    B．     C．      D．

2．(2021年高考全国甲卷理科)已知函数的部分图像如图所示，则满足条件的最小正整数x为________．

【考点总结与提高】

1.利用函数的图象研究函数的性质

对于已知或易画出其在给定区间上图象的函数，其性质（单调性、奇偶性、周期性、最值（值域）、零点）常借助图象研究，但一定要注意性质与图象特征的对应关系。

2.利用函数的图象研究不等式

当不等式问题不能用代数法求解.但其与函数有关时，常将不等式问题转化为两函数图象的上下关系问题，从而利用数形结合法求解。

3.利用函数的图象研究方程的根

当方程与基本初等函数有关时，可以通过函数图象来研究方程的根，方程的根就是函数的图象与轴的交点的横坐标，方程的根就是函数与图象的交点的横坐标。

【变式演练2】

1.已知函数，若函数有三个零点，则实数的取值范围是（       ）

A.         B.             C.          D.

2.已知上可导函数的图象如图所示，则不等式的解集为(     )

A.               B.

C.      D.

常考点03 函数的零点与方程的根

【典例3】

1.(2018全国卷Ⅲ)函数在的零点个数为_____．

2.（2019全国Ⅰ理11改编）关于函数在有_______个零点.

【考点总结与提高】

1.确定函数零点所在区间的方法

(1)解方程法：当对应方程f(x)＝0易解时，可先解方程，然后再看求得的根是否落在给定区间上。

(2)利用函数零点的存在性定理：首先看函数y＝f(x)在区间上的图象是否连续，再看是否有f(a)·f(b)＜0。若有，则函数y＝f(x)在区间(a，b)内必有零点。

(3)数形结合法：通过画函数图象，观察图象与x轴在给定区间上是否有交点来判断。

2.判断函数零点个数的方法

(1)解方程法：令f(x)＝0，如果能求出解，则有几个解就有几个零点。

(2)零点存在性定理法：利用定理不仅要求函数在区间[a，b]上是连续不断的曲线，且f(a)·f(b)＜0，还必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点或零点值所具有的性质。

(3)数形结合法：转化为两个函数的图象的交点个数问题，先画出两个函数的图象，看其交点个数，其中交点的横坐标有几个不同的值，就有几个不同的零点。

3.函数零点的应用问题类型及解题思路

(1)已知函数零点情况求参数。根据函数零点或方程的根所在的区间求解参数应分三步：

①判断函数的单调性；

②利用零点存在性定理，得到参数所满足的不等式；

③解不等式，即得参数的取值范围。

(2)已知函数零点的个数求参数，常利用数形结合法。

【变式演练3】

1.已知函数有唯一零点，则

A．  B．   C．  D．1

2.设函数，已知在有且仅有5个零点．的取值范围是____________.

【冲关突破训练】

1.函数的图像可能是（      )

2.函数 的图像可能为（   ）

3.函数的图象大致为 (　　)

4.已知为的导函数，则的图像是(    )

5.函数在的图象大致为 (　　)

6．（2019年高考浙江）在同一直角坐标系中，函数，(a>0，且a≠1)的图象可能是

7.下面四图都是在同一坐标系中某三次函数及其导函数的图像，其中一定不正确的序号是(　　 )

A．①②     B．③④      C．①③           D．①④

8．若函数在R上为减函数，则函数的图象可以是

A．    B．   C．  D．

9.定义在上的奇函数，当时，，则关于的函数的所有零点之和为（     ）

  A.              B.              C.             D.

10.若函数的图象如图所示，则下列函数图象正确的是

11．已知函数．

(1)讨论的单调性；(2)若有两个零点，求的取值范围．

12.（2019全国Ⅰ理20（2））已知函数，为的导数．证明：（2）有且仅有2个零点．