2021年河北省石家庄市九年级上学期数学期中试卷含答案

这是一份2021年河北省石家庄市九年级上学期数学期中试卷含答案，共13页。试卷主要包含了单项选择题，解答题等内容，欢迎下载使用。
 九年级上学期数学期中试卷
一、单项选择题
1.假设关于 的方程 是一元二次方程，那么 满足的条件是〔   〕
A.                                   B.                                   C.                                   D. 
2.学校为了了解全校学生的视力情况，从各年级共抽调了80名同学，对他们的视力进行调查，在这个调查活动中样本是〔　　〕
A. 80名同学的视力情况               B. 80名同学               C. 全校学生的视力情况               D. 全校学生
3.假设 ，那么 的值为〔   〕
A. 1                                          B.                                           C.                                           D. 
4.用配方法解方程 时，原方程变形为〔   〕
A.                       B.                       C.                       D. 
5.如图，小明在一条东西走向公路的O处，测得图书馆A在他的北偏东60°方向，且与他相距200m，那么图书馆A到公路的距离AB为(    )

A. 100m                          B. 100 m                          C. 100 m                          D. m
6.一组数据 的方差是2，那么另一组数据 的方差是〔    〕
A. 2                                           B. 3                                           C. 4                                           D. 5
7.某机械厂一月份生产零件50万个，第一季度生产零件200万个．设该厂二、三月份平均每月的增长率为x，那么x满足的方程是〔    〕
A.                                                 B. 
C.                       D. 
8.如图， 与 是位似图形，位似中心为 ， ， ，那么 的面积为〔   〕

A. 12                                         B. 16                                         C. 21                                         D. 49
9.如图，直线l1 l2 l3 ， 分别交直线m、n于点A、B、C、D、E、F ． 假设AB∶BC＝5∶3，DE＝15，那么EF的长为〔　　〕

A. 6                                          B. 9                                          C. 10                                          D. 25
10.小刚在解关于x的方程 时，只抄对了 ， ，解出其中一个根是 ．他核对时发现所抄的c比原方程的c值小2．那么原方程的根的情况是〔    〕
A. 不存在实数根                                                     B. 有两个不相等的实数根                 
C. 有一个根是x                                                       D. 有两个相等的实数根
11.如图，河坝横断面迎水坡AB的坡比为1： ，坝高BC＝3m，那么AB的长度为〔   〕

A. 6m                                   B. 3 m                                   C. 9m                                   D. 6 m
二、填空题
12.一组数据2，3，4，x ， 6的平均数是4，那么x是________．
13.关于x的一元二次方程 的一个根为 ，那么k的值是________．
14.设m、n是方程x2+x－1001＝0的两个实数根，那么m2+2m+n的值为________.
15.如图，点P是 中 边上的一点，请你添加一个条件使 ：________.

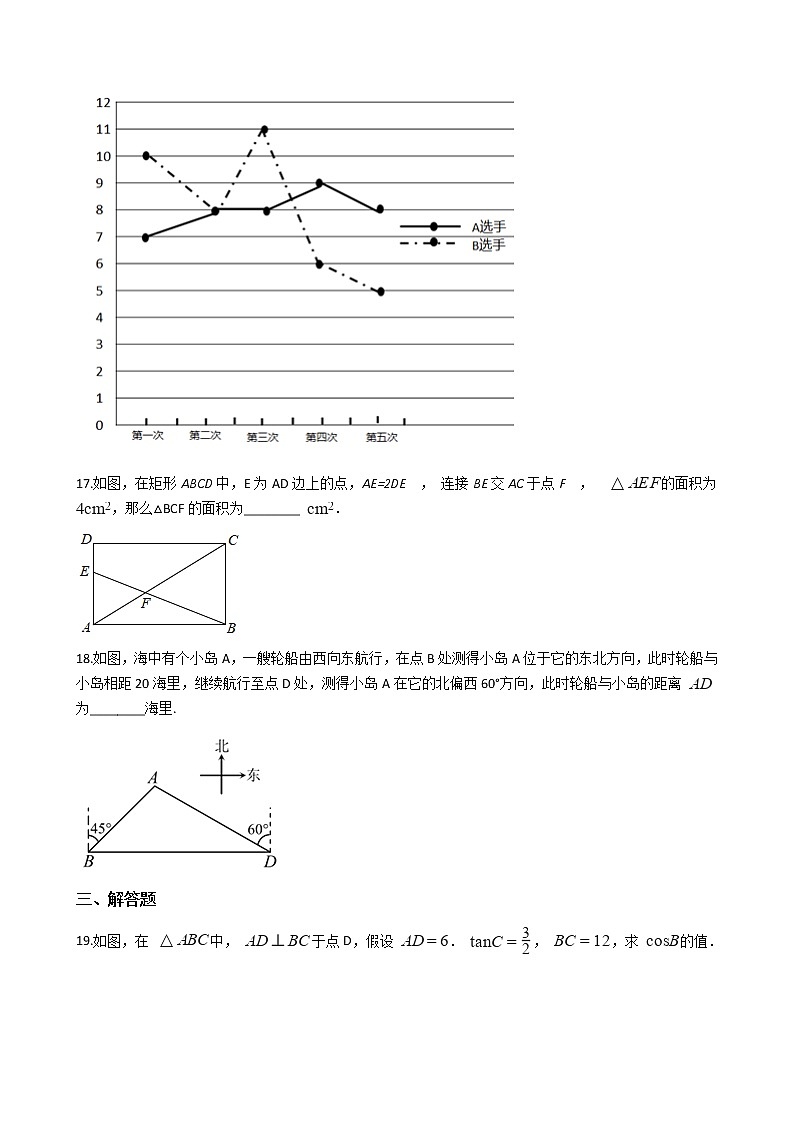
16.2022年将在北京——张家口举办冬季奥运会，北京将成为世界上第一个既举办夏季奥运会，又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛，为此对这两名队员进行了五次测试，测试成绩如下列图，________选手的成绩更稳定.

17.如图，在矩形ABCD中，E为AD边上的点，AE=2DE ， 连接BE交AC于点F ， 的面积为 ，那么△BCF的面积为________ ．

18.如图，海中有个小岛A，一艘轮船由西向东航行，在点B处测得小岛A位于它的东北方向，此时轮船与小岛相距20海里，继续航行至点D处，测得小岛A在它的北偏西60°方向，此时轮船与小岛的距离 为________海里.

三、解答题
19.如图，在 中， 于点D，假设 ． ， ，求 的值．

20.如图，有一块矩形硬纸板，长 ，宽 .在其四角各剪去一个同样的正方形，然后将四周突出局部折起，可制成一个无盖长方体盒子.当剪去正方形的边长取何值时，所得长方体盒子的侧面积为 ？

21.如图，小明用自制的直角三角形纸板DEF测量树的高度AB.他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上，纸板的两条直角边DE=40cm.EF=30cm，测得边DF离地面的高度AC=1.5m，CD=10m，求树高AB.

22.为了让同学们了解自己的体育水平，初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试〔得分均为整数〕，成绩总分值为10分，1班的体育委员根据这次测试成绩，制作了统计图和分析表如下：

初二1班体育模拟测试成绩分析表

平均分
方差
中位数
众数
男生
　   　
2
8
7
女生
7.92
1.99
8
　   　
根据以上信息，解答以下问题：
〔1〕这个班共有男生________人，共有女生________人；
〔2〕补全初二1班体育模拟测试成绩分析表；
〔3〕你认为在这次体育测试中，1班的男生队、女生队哪个表现更突出一些？并说明理由．〔至少从两个不同的角度说明推断的合理性〕
23. ， 是一元二次方程 的两个实数根．
〔1〕求k的取值范围；
〔2〕是否存在实数k，使得等式 成立？如果存在，请求出k的值，如果不存在，请说明理由．
24.一艘渔船从位于A海岛北偏东60°方向，距A海岛60海里的B处出发，以每小时30海里的速度沿正南方向航行．在A海岛周围50海里水域内有暗礁．〔参考数据： 〕

〔1〕这艘渔船在航行过程中是否有触礁的危险？请说明理由．
〔2〕渔船航行3小时后到达C处，求A ， C之间的距离．
25.如图，Rt△ABC，∠C＝90°，AC＝10cm，BC＝8cm．点P从点C出发，以2cm/s的速度沿CA向点A匀速运动，同时点Q从点B出发，以1cm/s的速度沿BC向点C匀速运动，当一个点到达终点时，另一个点随之停止．

〔1〕.求经过几秒后，△PCQ的面积等于△ABC面积的 ？
〔2〕.经过几秒，△PCQ与△ABC相似？

答案解析局部
一、单项选择题
1.【答案】 C
【解析】【解答】∵关于 的方程 是一元二次方程，
∴ ，
故答案为：C.
【分析】一元二次方程必须满足的条件：①一个未知数且未知数的最高次数是2；②二次项系数不为0；③整式方程，据此解答即可.
2.【答案】 A
【解析】【解答】解：学校为了了解全校学生的视力情况，从各年级共抽调了80名同学，对他们的视力进行调查，在这个调查活动中样本是80名同学的视力情况．
故答案为：A．
【分析】样本就是从总体中取出的一局部个体，根据定义即可求解．
3.【答案】 B
【解析】【解答】解：∵ ，
∴ ，
故答案为：B.
【分析】先把要求的式子进行化简，再把 代入进行计算即可.
4.【答案】 C
【解析】【解答】解：方程配方得：x2+6x+5+4-5=0，即〔x+3〕2=5．
故答案为：C．
【分析】方程整理后，配方得到结果，即可做出判断．
5.【答案】 A
【解析】【解答】解：∵AB⊥OB，∠AOB=90°-60°=30°，
∴AB=OA=100m.
故答案为：A.

【分析】先求出∠AOB的度数，再由30°所对的直角边的性质求解即可.
6.【答案】 A
【解析】【解答】解：∵数据x1 ， x2 ， …，xn的方差是2，
∴由于另一组数据x1+3，x2+3，…，xn+3是在原数据根底上每个数据都加上3，
∴新数据的波动幅度没有发生改变，
∴另一组数据x1+3，x2+3，…，xn+3的方差是2，
故答案为：A．
【分析】根据方差的定义求解可得．
7.【答案】 C
【解析】【解答】解：依题意得二、三月份的产量为 、 ，
．
故答案为：C．
【分析】一般增长后的量 增长前的量×〔1+增长率〕，如果该厂二、三月份平均每月的增长率为x，那么可以用x分别表示二、三月份的产量，然后根据题意可得出方程．
8.【答案】 D
【解析】【解答】解：∵ABC与△DEF是位似图形，位似中心为O，OA：AD=3：4，
∴OA：OD=3：7，
∴S△ABC：S△DEF=9：49，
∵S△ABC=9，
∴△DEF的面积为：49.
故答案为：D.
【分析】直接利用位似图形的性质得出位似比，进而根据面积比等于位似比的平方得出面积比，即可得出答案.
9.【答案】 B
【解析】【解答】解：∵l1∥l2∥l3 ， DE=15，
∴ ，即 ，
解得，EF=9，
故答案为：B．
【分析】根据平行线分线段成比例可得， 据此求出EF的长即可.
10.【答案】 A
【解析】【解答】解：∵小刚在解关于x的方程 ( )时，只抄对了 ， ，解出其中一个根是 ，
∴ ，
解得： ，
∵核对时发现所抄的c比原方程的c值小2，
故原方程中 ，
那么 ，
那么原方程的根的情况是不存在实数根．
故答案为：A．
【分析】直接把数据代入进而得出c的值，再利用根的判别式求出答案．
11.【答案】 A
【解析】【解答】解：∵迎水坡AB的坡比为1： ，
∴ ，即 ，
解得，AC＝3 ，
由勾股定理得，AB 6〔m〕，
故答案为：A．

【分析】根据坡度的概念，计算得到AC，继而由勾股定理求出AB即可。
二、填空题
12.【答案】 5
【解析】【解答】解：∵数据2，3，4，x，6的平均数是4，
∴〔2+3+4+x+6〕÷5=4，
解得：x=5；
故答案为：5．
【分析】根据用平均数的定义列出算式，再进行计算即可得出答案．
13.【答案】 2
【解析】【解答】解：将x=﹣3代入方程 中，
得：2×9+3k﹣24=0，
解得：k=2，
故答案为：2．
【分析】直接将x=﹣3代入方程中，得到关于k的方程，然后解方程即可求得k值．
14.【答案】 1000
【解析】【解答】解：∵m、n是方程 的两个实数根，该一元二次方程，二次项系数a=1，一次项系数b=1，常数项c=-1001，
∴根据根与系数的关系，可得到 ，
又∵ ，∴ ，
∴ ，
故答案为：1000.
【分析】由于m、n是方程 的两个实数根，根据根与系数的关系可以得到m+n=-1，并且 ，然后把 变形为 ，把前面的值代入即可求出结果.
15.【答案】
【解析】【解答】解：∵∠B=∠B
∴当 时，
故答案为： ．
【分析】根据相似三角形的判定定理即可求解．
16.【答案】 A
【解析】【解答】解：根据统计图可得出：SA2＜SB2 ， 那么A选手的成绩更稳定，
故答案为：A．
【分析】根据方差的定义，方差越小数据越稳定．
17.【答案】 9
【解析】【解答】解：∵矩形ABCD
∴
∵
∴
∴
又∵矩形ABCD
∴
∴ 且
∴
∴
∵
∴
故答案为：9．
【分析】根据AE和DE的比例关系，结合矩形ABCD中 ，可求得AE和BC的比例关系；由 可推导出 ，再利用相似三角形面积比等于相似比的平方，完成求解．
18.【答案】
【解析】【解答】解：如图，过点A作AC⊥BD，

依题意可得∠ABC=45°
∴△ABC是等腰直角三角形，AB=20(海里)
∴AC=BC=ABsin45°=10 (海里)
在Rt△ACD中，∠ADC=90°-60°=30°
∴AD=2AC=20 (海里)
故答案为：20 .
【分析】过点A作AC⊥BD，根据方位角及三角函数即可求解.
三、解答题
19.【答案】 解：

，
．
．
在 中
，

【解析】【分析】在 中，利用正切定义解得CD的长，结合条件，可得BD的长，再由勾股定理解题即可．
20.【答案】 解：设剪去正方形的边长为 ，那么做成无盖长方体盒子的底面长为 ，宽为 ，高为 ，
依题意，得： ，
整理，得： ，
解得： ， ，
当 时， ，不合题意，舍去，
∴ ，
答：当剪去正方形的边长为 cm时，所得长方体盒子的侧面积为
【解析】【分析】 设剪去正方形的边长为 ，那么做成无盖长方体盒子的底面长为 ，宽为 ，高为 ， 根据矩形的面积计算方法，及长方体盒子侧面积的计算方法，由 长方体盒子的侧面积为 建立方程，求解并检验即可。
21.【答案】 解：∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴ ，
∵DE=40cm=0.4m，EF=30cm=0.3m，AC=1.5m，CD=10m，
∴ ，
∴BC=7.5米，
∴AB=AC+BC=1.5+7.5=9米.
【解析】【分析】首先根据两组角对应相等的两个直角三角形相似得出 △DEF∽△DCB ，根据相似三角形对应边成比例得出 ，利用比例式求得BC的长后加上小明同学的身高即可求得树高AB.
22.【答案】 〔1〕20；25
〔2〕解：男生的平均分为 ×〔5+6×2+7×6+8×3+9×5+10×3〕＝7.9〔分〕，女生的众数为8分，
补全表格如下：

　平均分
　方差
　中位数
　众数
　男生
7.9
　2
　8
　7
　女生
　7.92
　1.99
　8
8

〔3〕解：我认为女生队表现更突出．
理由为：女生队的平均数较高，表示女生队测试成绩较好；
女生队的方差小，表示女生队测试成绩比较集中，整体水平较好；
女生队的众数较高，女生队的众数为8，中位数也为8，而男生队众数为7低于中位数8，表示女生队的测试成绩高分较多．
【解析】【解答】解：〔1〕这个班共有男生1+2+6+3+5+3＝20〔人〕，共有女生45﹣20＝25〔人〕，
故答案为：20、25；
【分析】〔1〕由条形图可得男生总人数，总人数减去男生人数可得女生人数；〔2〕根据平均数和众数定义可得．〔3〕可从平均数、方差、众数和中位数的意义求解可得．
23.【答案】 〔1〕解：∵一元二次方程有两个实数根，
∴
解得 ；

〔2〕解：由一元二次方程根与系数关系，
∵ ，
∴
即 ，解得 ．
又由〔1〕知： ，
∴ ．
【解析】【分析】〔1〕根据方程的系数结合 ≥0，即可得出关于k的一元一次不等式，解之即可得出k的取值范围；〔2〕根据根与系数的关系可得出x1＋x2＝2，x1x2＝k＋2，结合 ，即可得出关于k的方程，解之即可得出k值，再结合〔1〕即可得出结论．
24.【答案】 〔1〕解：过A点作 于点D，

∴ ，
由题意可得 ，
∴在 中， ，
∴渔船在航行过程中没有触礁的危险；

〔2〕解：在 中， ，
∵ ，
∴ ，
在 中， ，
即A，C之间的距离为79.50海里.
【解析】【分析】〔1〕过A点作 于点D ， 在 中求出AD与50海里比较即可得到答案；〔2〕在 中求出BD得到CD，再根据勾股定理求出AC.
25.【答案】 〔1〕解：设经过x秒，△PCQ的面积等于△ABC面积的 ，
，
解得：x1＝x2＝4，
答：经过4秒后，△PCQ的面积等于△ABC面积的 ；

〔2〕解：设经过t秒，△PCQ与△ABC相似，
因为∠C＝∠C，所以分为两种情况：
① ，
，解得：t ；
② ，
，解得：t ；
答：经过 秒或 秒时，△PCQ与△ABC相似．
【解析】【分析】〔1〕分别表示出线段PC和线段CQ的长后利用S△PCQ= S△ABC列出方程求解；〔2〕设运动时间为t s，△PCQ与△ACB相似，当△PCQ与△ACB相似时，那么有 或 ，分别代入可得到关于t的方程，可求得t的值．