2021年黑龙江省齐齐哈尔市九年级上学期数学期中试卷含答案

这是一份2021年黑龙江省齐齐哈尔市九年级上学期数学期中试卷含答案，共15页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。

 九年级上学期数学期中试卷
一、单项选择题
1.以下列图形中，既是轴对称图形又是中心对称图形的是 　　
A.                                 B.                                 C.                                 D. 
2.抛物线 的顶点坐标是〔　　〕
A. 〔0，3〕                        B. 〔3，0〕                        C. 〔0，﹣3〕                        D. 〔﹣3，0〕
3.假设关于 的一元二次方程 的常数项为0，那么m的值等于〔    〕
A. 1                                          B. 2                                          C. 1或2                                          D. 0
4.将抛物线y=x2﹣4x﹣4向左平移3个单位，再向上平移5个单位，得到抛物线的函数表达式为〔   〕
A. y=〔x+1〕2﹣13          B. y=〔x﹣5〕2﹣3          C. y=〔x﹣5〕2﹣13          D. y=〔x+1〕2﹣3
5.在一个有10万人的小镇，随机调查了1000人，其中有120人周六早上观看中央电视台的“朝闻天下〞节目，那么在该镇随便问一个人，他在周六早上观看中央电视台的“朝闻天下〞节目的概率大约是〔   〕
A.                                    B.                                    C.                                    D. 
6.过⊙O内一点M的最长弦长为10 cm ， 最短弦长为8 cm ， 那么OM为(   )
A. 6 cm                                  B. 3 cm                                  C. cm                                  D. 9 cm
7.某超市一月份的营业额为200万元,第一季度的总营业额共1000万元, 如果平均每月增长率为x,那么由题意列方程应为(    )

A. 200(1+x)2=1000                                               B. 200+200×2x=1000
C. 200+200×3x=1000                                          D. 200[1+(1+x)+(1+x)2]=1000
8.在同一直角坐标系中，函数y＝mx+m和函数y＝mx2+2x+2〔m是常数，且m≠0〕的图象可能是〔    〕
A.                B.                C.                D. 
9.如图，AB为⊙O的直径，弦CD⊥AB于E，CD=12，BE=2，那么⊙O的半径为〔　　〕

A. 8                                         B. 10                                         C. 16                                         D. 20
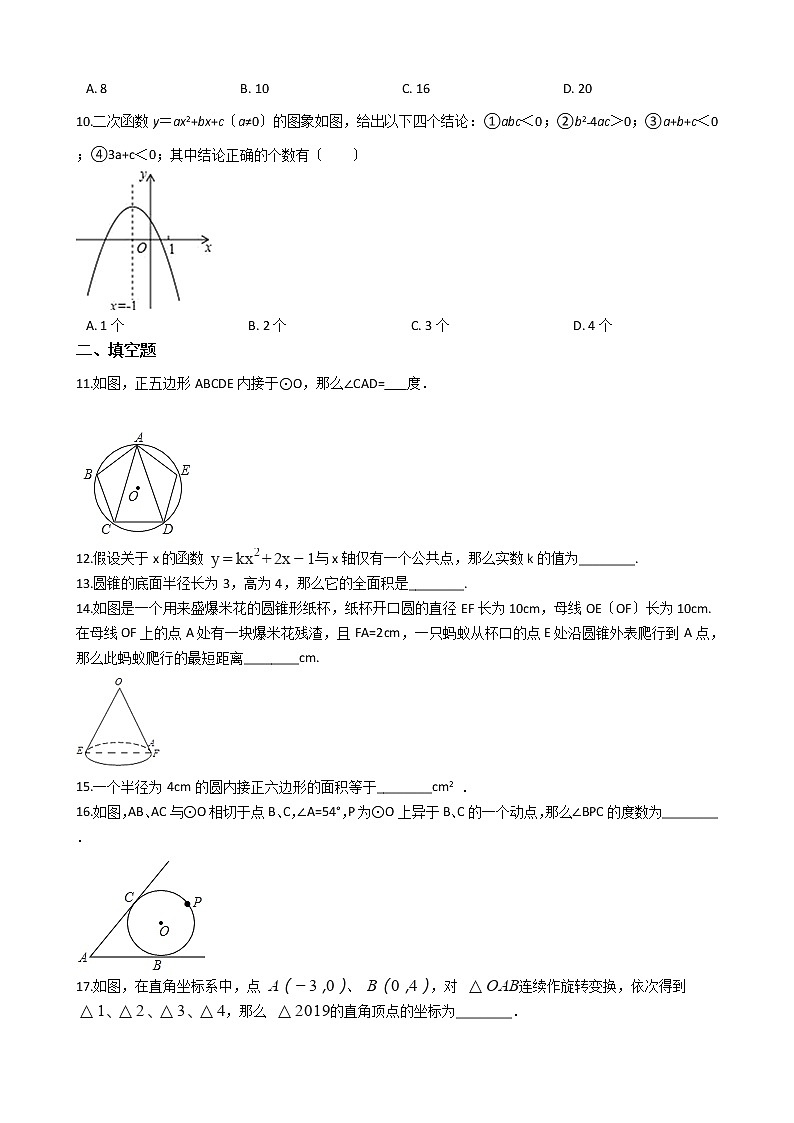
10.二次函数y＝ax2+bx+c〔a≠0〕的图象如图，给出以下四个结论：①abc＜0；②b2﹣4ac＞0；③a+b+c＜0；④3a+c＜0；其中结论正确的个数有〔　　〕

A. 1个                                       B. 2个                                       C. 3个                                       D. 4个
二、填空题
11.如图，正五边形ABCDE内接于⊙O，那么∠CAD=       度．


12.假设关于x的函数 与x轴仅有一个公共点，那么实数k的值为________.
13.圆锥的底面半径长为3，高为4，那么它的全面积是________.
14.如图是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径EF长为10cm，母线OE〔OF〕长为10cm.在母线OF上的点A处有一块爆米花残渣，且FA=2cm，一只蚂蚁从杯口的点E处沿圆锥外表爬行到A点，那么此蚂蚁爬行的最短距离________cm.

15.一个半径为4cm的圆内接正六边形的面积等于________cm2 ．
16.如图，AB、AC与⊙O相切于点B、C，∠A=54°，P为⊙O上异于B、C的一个动点，那么∠BPC的度数为________．

17.如图，在直角坐标系中，点 、 ，对 连续作旋转变换，依次得到 ，那么 的直角顶点的坐标为________．

三、解答题
18.二次函数的顶点坐标为〔4，－2〕，且其图象经过点〔5，1〕，求此二次函数的解析式．
19.解方程
〔1〕
〔2〕
20.如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A〔1，4〕，B〔4，2〕，C〔3，5〕〔每个方格的边长均为1个单位长度〕．

⑴请画出将△ABC向下平移5个单位后得到的△A1B1C1；
⑵将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A2B2C2 ， 并直接写出点B旋转到点B2所经过的路径长．
21.水果店张阿姨以每斤2元的价格购进某种水果假设干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出260斤，张阿姨决定降价销售．

〔1〕假设将这种水果每斤的售价降低x元，那么每天的销售量是　________ 斤。〔用含x的代数式表示〕

〔2〕销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？

22.如图，AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠CAE=∠ADC．

〔1〕求证：AE是⊙O的切线；
〔2〕假设⊙O的半径为2，∠B=60°，求图中阴影局部的面积．〔结果保存根号和π〕
23.九〔1〕班针对“你最喜爱的课外活开工程〞对全班学生进行调查(每名学生分别选一个活开工程)，并根据调查结果列出统计表，绘制成扇形统计图.
男、女生所选工程人数统计表
工程
男生人数
女生人数
机器人
7
9
3D打印机
m
4
航模
2
2
其他
5
n

根据以上信息解决以下问题:
〔1〕________， ________;
〔2〕扇形统计图中机器人工程所对应扇形的圆心角度数为________°;
〔3〕从选航模工程的4名学生中随机选取2名学生参加学校航模兴趣小组训练，请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
24.如图，抛物线经过A〔﹣1，0〕，B〔5，0〕，C〔0， 〕三点．



〔1〕求抛物线的解析式；

〔2〕在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；

〔3〕点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？假设存在，求点N的坐标；假设不存在，请说明理由．


答案解析局部
一、单项选择题
1.【答案】 D
【解析】【解答】解：A、不是轴对称图形，是中心对称图形，故本选项不合题意；
B、不是轴对称图形，是中心对称图形，故本选项不合题意；
C、是轴对称图形，不是中心对称图形，故本选项不合题意；
D、是轴对称图形，也是中心对称图形，故本选项符合题意；
故答案为：D．
【分析】根据轴对称图形的性质、中心对称图形的性质逐项判断即可。
2.【答案】 A
【解析】【解答】解：抛物线 的顶点坐标是 〔0,3〕 ，
故答案为：A．
【分析】根据函数的草图即可判断出顶点坐标。
3.【答案】 B
【解析】【解答】解：由题意可知：常数项 且二次项系数 ，
当 时解得 ， ，
又 ，即
∴ ，
故答案为：B．
【分析】由题意得 且二次项系数 即可求解．
4.【答案】 D
【解析】【解答】解：因为y=x2﹣4x﹣4=〔x﹣2〕2﹣8，
所以抛物线y=x2﹣4x﹣4的顶点坐标为〔2，﹣8〕，把点〔2，﹣8〕向左平移3个单位，再向上平移5个单位所得对应点的坐标为〔﹣1，﹣3〕，所以平移后的抛物线的函数表达式为y=〔x+1〕2﹣3．
应选D．
【分析】先把一般式配成顶点式得到抛物线y=x2﹣4x﹣4的顶点坐标为〔2，﹣8〕，再利用点平移的规律得到把点〔2，﹣8〕平移后所得对应点的坐标为〔﹣1，﹣3〕，然后利用顶点式写出平移后的抛物线的函数表达式．
5.【答案】 C
【解析】【解答】解：由题意知：1000人中有120人看中央电视台的早间新闻，
∴在该镇随便问一人，他看早间新闻的概率大约是 ＝ ．
故答案为：C.

【分析】一步试验事件发生的概率的计算公式：P=〔n为该事件所有等可能出现的结果数，k为事件包含的结果数)。
6.【答案】 B
【解析】【解答】由可知，最长的弦是过M的直径AB
最短的是垂直平分直径的弦CD
AB=10cm，CD=8cm
那么OD=5cm，MD=4cm
由勾股定理得OM=3cm．
故答案为3cm．
【分析】根据垂径定理可解得.
7.【答案】 D
【解析】【分析】先得到二月份的营业额，三月份的营业额，等量关系为：一月份的营业额+二月份的营业额+三月份的营业额=1000万元，把相关数值代入即可．
∵一月份的营业额为200万元，平均每月增长率为x，
∴二月份的营业额为200×〔1+x)，
∴三月份的营业额为200×〔1+x)×〔1+x)=200×〔1+x)2 ，
∴可列方程为200+200×〔1+x)+200×〔1+x)2=1000，
即200[1+〔1+x)+〔1+x)2]=1000．
应选D．
【点评】假设设变化前的量为a，变化后的量为b，平均变化率为x，那么经过两次变化后的数量关系为a〔1±x)2=b．得到第一季度的营业额的等量关系是解决此题的关键．

8.【答案】 D
【解析】【解答】A、由函数y=mx+m的图象可知m＜0，那么函数y=-mx2+x+1开口方向朝上，与图象不符，故A不符合题意；
B、由函数y=mx+m的图象可知m＜0，那么函数y=-mx2+x+1开口方向朝上，对称轴为x=- ＝ ＜0，那么对称轴应在y轴左侧，与图象不符，故B不符合题意；
C、由函数y=mx+m的图象可知m＞0，那么函数y=-mx2+x+1开口方向朝下，与图象不符，故C不符合题意；
D、由函数y=mx+m的图象可知m＜0，那么函数y=-mx2+x+1开口方向朝上，对称轴为x=- ＝ ＜0，那么对称轴应在y轴左侧，与图象符合，故D符合题意.
故答案为：D.
【分析】由直线经过的象限可知m＜0，那么抛物线开口向下，对称轴在y轴的右侧；
9.【答案】 B
【解析】【解答】解：连结OC ， 如图，

设⊙O半径为r ， 那么OC＝r ， OE＝r﹣BE＝r﹣2，
∵CD⊥AB ，
∴CE＝DE＝ CD＝6，
在Rt△OCE中，∵OE2+CE2＝OC2 ，
∴〔r﹣2〕2+62＝r2 ， 解得：r＝10，即⊙O半径为10．
故答案为：B．
【分析】连接OC，利用垂径定理及勾股定理计算半径即可。
10.【答案】 C
【解析】【解答】解：①由开口向下，可得a＜0，又由抛物线与y轴交于正半轴，可得c＞0，
∵-
∴abc＞0，故①不符合题意；
②∵抛物线和x轴两个交点，
∴b2-4ac＞0，故②符合题意；
③令x=1，∴y=a+b+c＜0，故③符合题意；
④∵ ，a+b+c＜0，
∴3a+c＜0；故④符合题意；
故答案为：C．
【分析】先根据函数图像，判断出二次函数次数的正负性，再利用二次函数的图形和性质逐项判断即可。
二、填空题
11.【答案】 36
【解析】【解答】解：∵五边形ABCDE是正五边形，

∴=====72°，
∴∠CAD=×72°=36°．故答案为36．
【分析】圆内接正五边形ABCDE的顶点把圆五等分，即可求得五条弧的度数，根据圆周角的度数等于所对的弧的度数的一半即可求解．
12.【答案】 0或－1
【解析】【解答】解：由于没有交待是二次函数，故应分两种情况：
当k=0时，函数 是一次函数，与x轴仅有一个公共点；
当k≠0时，函数 是二次函数，假设函数与x轴仅有一个公共点，那么 有两个相等的实数根，即 ；
综上所述，假设关于x的函数 与x轴仅有一个公共点，那么实数k的值为0或－1.
故答案为：0或－1.
【分析】由于没有交待是二次函数，故应分两种情况：当k=0时，该函数是一次函数，其图形与x轴有且只有一个交点；当k≠0时，该函数是二次函数，假设函数与x轴仅有一个公共点，那么方程 有两个相等的实数根，故该方程根的判别式的值应该等于0，从而列出方程，求解即可得出k的值.
13.【答案】
【解析】【解答】解：由题意，圆锥的母线长= ，所以圆锥的侧面积= ，
∴这个圆锥的全面积= .
故答案为： .
【分析】先利用勾股定理求出圆锥的母线长，再计算出其侧面积，进一步即可求出答案.
14.【答案】 cm
【解析】【解答】因为OE=OF=EF=10〔cm〕，
所以底面周长=10π〔cm〕，
将圆锥侧面沿OF剪开展平得一扇形，此扇形的半径OE=10〔cm〕，弧长等于圆锥底面圆的周长10π〔cm〕
设扇形圆心角度数为n，那么根据弧长公式得：
10π= ，
所以n=180°，
即展开图是一个半圆，
因为E点是展开图弧的中点，
所以∠EOF=90°，
连接EA，那么EA就是蚂蚁爬行的最短距离，

在Rt△AOE中由勾股定理得，
EA2=OE2+OA2=100+64=164，
所以EA=2 〔cm〕，
即蚂蚁爬行的最短距离是2 〔cm〕.
【分析】为求蚂蚁爬行的最短路径，需将圆锥的侧面展成平面图形，由两点之间线段最短可得蚂蚁爬行的最短路径，利用勾股定理计算即可.
15.【答案】
【解析】【解答】解：一个圆的内接正六边形可以分成6个全等的等边三角形，
∵圆的半径是4cm，
∴等边三角形的边长是4cm，
如图，

边长是4cm的等边三角形，
根据等边三角形的性质， ， ，
根据勾股定理， ，
，
∴内接正六边形的面积是 ．
故答案是： ．
【分析】根据草图，先算出正六边形的边长，再将正六边形分成六个正三角形，算出其中一个小三角形的面积再乘六即可。
16.【答案】 63°或117°
【解析】【解答】解：∵AB、AC与⊙O相切于点B、C，
 ．
∵四边形内角和为360°，∠A=54°，
 ．
当点P在优弧BC上时，
，；
当点P在劣弧BC上时，
，
故答案为：63°或117°．
【分析】连接CO、BO，再根据四边形内角和及切线的性质求出的度数，再根据圆周角的性质求出角P即可。
17.【答案】
【解析】【解答】解：∵点A〔-3，0〕、B〔0，4〕，
∴AB= =5，
由图可知，每三个三角形为一个循环组依次循环，一个循环组前进的长度为：4+5+3=12，
∵2021÷3=673，
∴△2021的直角顶点是第673个循环组的最后一个三角形的直角顶点，
∵673×12=8076，
∴△2021的直角顶点的坐标为〔8076，0〕．
故答案为〔8076，0〕.
【分析】此题是一个循环规律题，需要先求出前几个点坐标，再通过观察归纳总结结论。
三、解答题
18.【答案】 解：设此二次函数的解析式为 ．
∵其图象经过点〔5，1〕，
∴ ，
∴ ，
∴ ．
【解析】【分析】此题利用顶点式求二次函数表达式，设， 再将嗲〔5，1〕代入计算即可。
19.【答案】 〔1〕解：
．

〔2〕解：
．
【解析】【分析】〔1〕先将所有的项移到等于号左边，再利用因式分解法解答即可；〔2〕此题采用公式法求解即可。
20.【答案】 解：〔1〕如图，△A1B1C1为所作；〔2〕如图，△A2B2C2为所作，
OB＝ ＝2
点B旋转到点B2所经过的路径长＝ ＝ π

【解析】【分析】〔1〕先画出A、B、C三点平移后的点坐标，再连接即可；〔2〕先画出A、B、C三点绕原点O逆时针旋转90度后的对应点，再连接即可；利用弧长公式求点B旋转经过的路径长。
21.【答案】 〔1〕100+200x
〔2〕解：根据题意得：〔4﹣2﹣x〕〔100+200x〕=300，解得：x=​或x=1，∵ 每天至少售出260斤，∴ x=1
答：张阿姨需将每斤的售价降低1元．
【解析】【解答】〔1〕将这种水果每斤的售价降低x元，那么每天的销售量是100+x0.1×20=〔100+200x〕斤； 〔2〕根据题意得：

〔4-2-x〕〔100+200x〕=300，解得：x=​或x=1，∵ 每天至少售出260斤，∴ x=1    故答案为：张阿姨需将每斤的售价降低1元．
【分析】〔1〕销售量=原来销售量+下降销售量，据此列式即可；〔2〕根据销售量×每斤利润=总利润列出方程求解即可．
22.【答案】 〔1〕证明：∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠B+∠BAC=90°，
∵∠B=∠ADC=∠CAE，
∴∠BAE=∠BAC+∠EAC=∠BAC+∠B=90°，
∴ BA⊥AE，
∴AE是⊙O的切线．

〔2〕解：作OM⊥AC，垂足为M．

∵∠B=60°，
∴∠AOC=2∠B=120°，
∴∠AOM=∠COM=60°，    
∴OM= AO=1，
∴AM= ，
∴AC=2AM= ，
∴S阴=S扇形AOC-S△AOC= ．
【解析】【分析】〔1〕此题的关键是证出∠BAE=∠BAC+∠EAC=90°，需要利用圆周角证出∠B=∠ADC=∠CAE，再利用直径所对的圆周角为直角，转化即可；〔2〕此题利用“割补法〞，用扇形OAC的面积减去三角形OAC的面积即可。
23.【答案】 〔1〕；
〔2〕144
〔3〕解：将选航模工程的 名男生编上号码 ，将 名女生编上号码 . 用表格列出所有可能出现的结果：
第一个
第二个
1
2
3
4
1

〔2,1〕
〔3,1〕
〔4,1〕
2
〔1,2〕

〔3,2〕
〔4,2〕
3
〔1,3〕
〔2,3〕

〔4,3〕
4
〔1,4〕
〔2,4〕
〔3,4〕

由表格可知，共有 种可能出现的结果，并且它们都是第可能的，其中“ 名男生、 名女生〞有 种可能. (  名男生、 名女生) .(如用树状图，酌情相应给分)
【解析】【分析】〔1〕先利用“航模〞求出总人数，再分别求m、n的值；〔2〕用“机器人〞的总人数除以参加男女总人数再乘即可；〔3〕通过列表法或树状图求出所有情况，再用符合要求的情况除以总情况数即可。
24.【答案】 〔1〕解：设抛物线的解析式为y=ax2+bx+c〔a≠0〕，

∵A〔﹣1，0〕，B〔5，0〕，C〔0， 〕三点在抛物线上，
∴ ，
解得 ．
∴抛物线的解析式为：y= x2﹣2x﹣

〔2〕解：∵抛物线的解析式为：y= x2﹣2x﹣ ，

∴其对称轴为直线x=﹣ =﹣ =2，
连接BC，如图1所示，

∵B〔5，0〕，C〔0，﹣ 〕，
∴设直线BC的解析式为y=kx+b〔k≠0〕，
∴ ，
解得 ，
∴直线BC的解析式为y= x﹣ ，
当x=2时，y=1﹣ =﹣ ，
∴P〔2，﹣ 〕

〔3〕解：存在．

如图2所示，

①当点N在x轴下方时，
∵抛物线的对称轴为直线x=2，C〔0，﹣ 〕，
∴N1〔4，﹣ 〕；
②当点N在x轴上方时，
如图，过点N2作N2D⊥x轴于点D，
在△AN2D与△M2CO中，

∴△AN2D≌△M2CO〔ASA〕，
∴N2D=OC= ，即N2点的纵坐标为 ．
∴ x2﹣2x﹣ = ，
解得x=2+ 或x=2﹣ ，
∴N2〔2+ ， 〕，N3〔2﹣ ， 〕．
综上所述，符合条件的点N的坐标为〔4，﹣ 〕，〔2+ ， 〕或〔2﹣ ， 〕．
【解析】【分析】〔1〕设抛物线的解析式为y=ax2+bx+c〔a≠0〕，再把A〔﹣1，0〕，B〔5，0〕，C〔0，- 〕三点代入求出a、b、c的值即可；〔2〕因为点A关于对称轴对称的点B的坐标为〔5，0〕，连接BC交对称轴直线于点P，求出P点坐标即可；〔3〕分点N在x轴下方或上方两种情况进行讨论．