华师大版八年级上册第13章 全等三角形综合与测试单元测试精练

这是一份华师大版八年级上册第13章 全等三角形综合与测试单元测试精练，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
八年级上数学检测卷
第14章 勾股定理（二）
时间：100分钟 满分：100分 得分：
一、选择题（每小题2分，共28分）
在下列各题的四个备选答案中，只有一个是正确的，请把你认为正确的答案的字母代号填写在下表相应题号的方格内.
题 号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
答 案














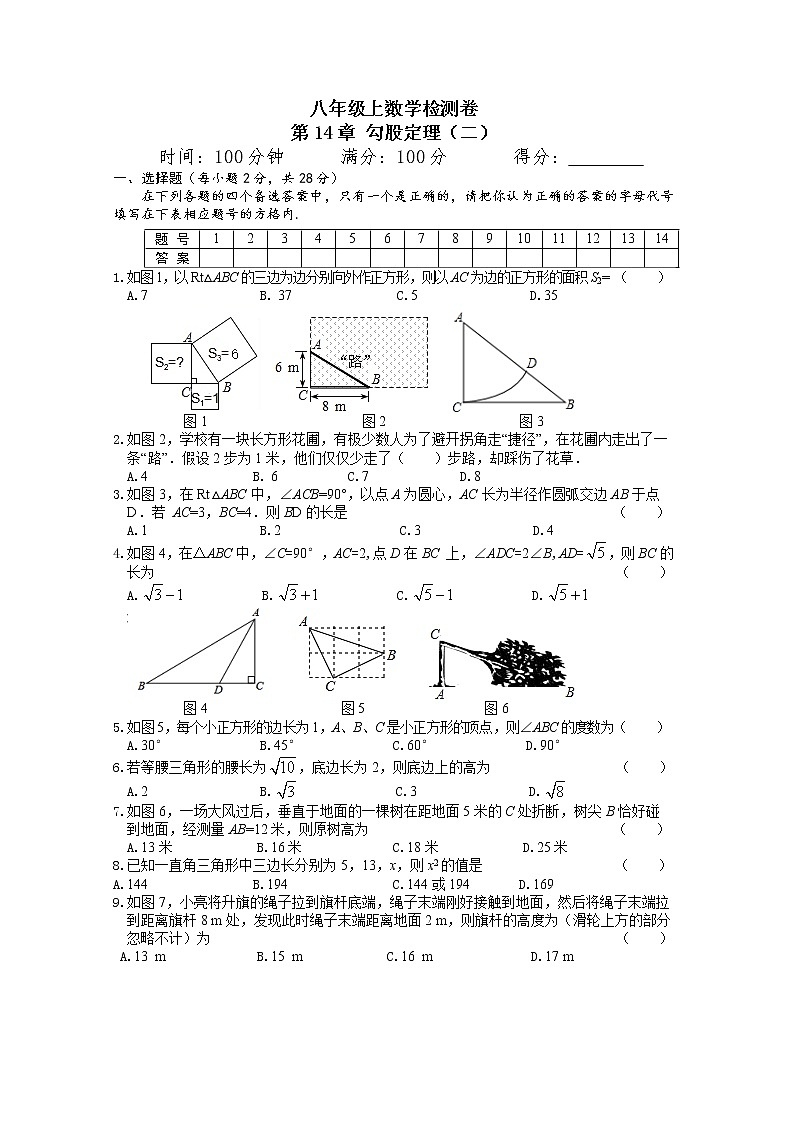
1.如图1，以Rt△ABC的三边为边分别向外作正方形，则以AC为边的正方形的面积S2= （ ）
A.7 B. 37 C.5 D.35

图1 图2 图3
2.如图2，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．假设2步为1米，他们仅仅少走了（ ）步路，却踩伤了花草．
A.4 B. 6 C.7 D.8
3.如图3，在Rt△ABC中，∠ACB=90°，以点A为圆心，AC长为半径作圆弧交边AB于点D．若  AC=3，BC=4．则BD的长是 （ ）
A.1 B.2 C.3 D.4
4.如图4，在△ABC中，∠C=90°，AC=2,点D在BC 上，∠ADC=2∠B,AD=，则BC的长为 （ ）
A. B. C. D.

图4 图5 图6
5.如图5，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为（ ）
A.30° B.45° C.60° D.90°
6.若等腰三角形的腰长为，底边长为2，则底边上的高为 （ ）
A.2 B. C.3 D.
7.如图6，一场大风过后，垂直于地面的一棵树在距地面5米的C处折断，树尖B恰好碰到地面，经测量AB=12米，则原树高为 （ ）
A.13米 B.16米 C.18米 D.25米
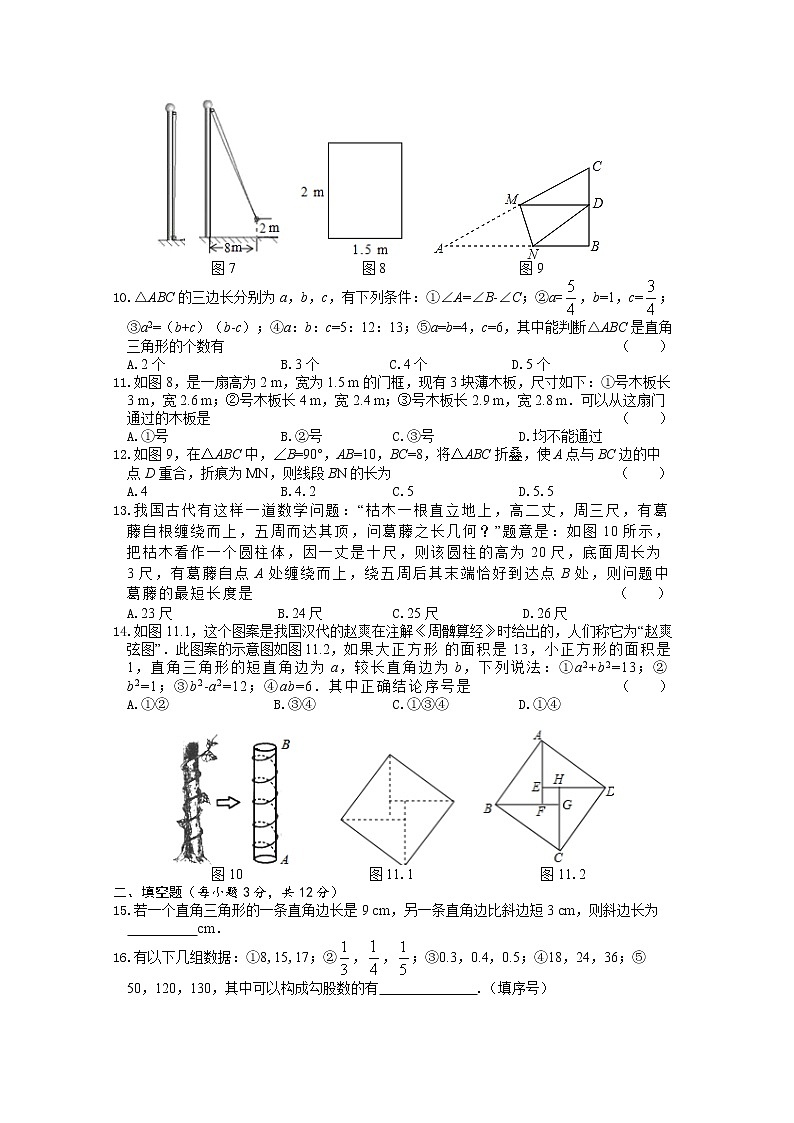
8.已知一直角三角形中三边长分别为5，13，x，则x2的值是 （ ）
A.144 B.194 C.144或194 D.169
9.如图7，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8 m处，发现此时绳子末端距离地面2 m，则旗杆的高度为（滑轮上方的部分忽略不计）为 （ ）
A.13 m B.15 m C.16 m D.17 m

图7 图8 图9
10.△ABC的三边长分别为a，b，c，有下列条件：①∠A=∠B-∠C；②a=，b=1，c=；③a2=（b+c）（b-c）；④a：b：c=5：12：13；⑤a=b=4，c=6，其中能判断△ABC是直角三角形的个数有 （ ）
A.2个 B.3个 C.4个 D.5个
11.如图8，是一扇高为2 m，宽为1.5 m的门框，现有3块薄木板，尺寸如下：①号木板长3 m，宽2.6 m；②号木板长4 m，宽2.4 m；③号木板长2.9 m，宽2.8 m．可以从这扇门通过的木板是 （ ）
A.①号 B.②号 C.③号 D.均不能通过
12.如图9，在△ABC中，∠B=90°，AB=10，BC=8，将△ABC折叠，使A点与BC边的中点D重合，折痕为MN，则线段BN的长为 （ ）
A.4 B.4.2 C.5 D.5.5
13.我国古代有这样一道数学问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图10所示，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则问题中葛藤的最短长度是 （ ）
A.23尺 B.24尺 C.25尺 D.26尺
14.如图11.1，这个图案是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．此图案的示意图如图11.2，如果大正方形 的面积是13，小正方形的面积是1，直角三角形的短直角边为a，较长直角边为b，下列说法：①a2+b2=13；②b2=1；③b2-a2=12；④ab=6．其中正确结论序号是 （ ）
A.①② B.③④ C.①③④ D.①④


图10 图11.1 图11.2
二、填空题（每小题3分，共12分）
15.若一个直角三角形的一条直角边长是9 cm，另一条直角边比斜边短3 cm，则斜边长为
cm．
16.有以下几组数据：①8,15,17；②，，；③0.3，0.4，0.5；④18，24，36；⑤ 50，120，130，其中可以构成勾股数的有 .（填序号）
17.如图12，将一根长24 cm的筷子，置于底面半径为2.5 cm，高为12 cm的圆柱形水杯中，设筷子露在杯子外面的长度为h cm，则h的取值范围是 .

图12 图13
18.如图13，在△ABC中，AB=AC=6，点M是BC边上不与点B,C重合的动点，则AM2+MB·MC= .
三、解答题（共60分）
19.（6分）用反证法证明：在一个三角形中，至少有两个内角是锐角．



20.（9分）如图14，在4×3的正方形网格中，每个小正方形的边长都是1
（1）分别求出线段AB，CD的长度；
（2）在图中画线段EF，使EF的长为，并判断AB、CD、EF三条线段能否构成直角三
角形．

图14
21.（9分）如图15，一架长为5米的梯子AB斜靠在与地面OM垂直的墙ON上，梯子底端距离墙ON有3米．
（1）求梯子顶端与地面的距离OA的长．
（2）若梯子顶点A下滑1米到C点，求梯子的底端向右滑多少米．

图15
22.（10分）如图16，把一块等腰直角三角形零件（△ABC，其中∠ACB=90°），放置在一凹槽内，三个顶点A，B，C分别落在凹槽内壁上，已知∠ADE=∠BED=90°，测得AD=5 cm，BE=12cm，求该三角形零件的面积．

图16
23.（12分）按照有关规定：距高铁轨道 200 米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物．如图17是一个小区平面示意图，矩形ABEF为一新建小区，直线MN为高铁轨道，C，D是直线MN上的两点，点C，A，B在一直线上，且DA⊥CA，AD=240米，AC=320米．小玲准备购买①号楼A单元的一套住宅.
（1）请你帮小玲算一算A单元的住户是否会受到噪声影响，并说明理由；
（2）若一列长度为228米的高铁以252千米/小时的速度通过时，则A单元用户受到影响时间有多长？

图17


24.（14分）如图18，在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积．某学习小组经过合作交流，给出了下面的解题思路：

（1）请你按照他们的解题思路完成解答过程．
（2）若点P在直线BC上，当△APC为直角三角形时，求CP的长．








参考答案及评分标准
一、CDBDB CCCDC BBCD
二、15.15 16.①③⑤ 17.11≤h≤12 18.36
三、19.证明： ①假设△ABC中只有一个角是锐角，不妨设∠A＜90°，∠B≥90°，∠C≥90°；于是，∠A＋∠B＋∠C＞180°，这与三角形内角和定理相矛盾；②假设△ABC中没有一个角是锐角，不妨设∠A≥90°，∠B≥90°，∠C≥90°；于是，∠A＋∠B＋∠C＞180°，这与三角形内角和定理相矛盾.所以，在一个三角形中，至少有两个角是锐角. …（6分）
20.解：（1）AB==； …（2分）
CD==． …（4分）
（2）线段EF如图所示. …（6分）
注：画图方式不唯一，符合题意即可.

∵AB=；CD=,EF=
∴CD2+EF2=8+5=13=AB2，
∴AB，CD，EF三条线能构成直角三角形． …（9分）
21.解：（1）在Rt△AOB中，由勾股定理得AO==4（米）； …（4分）
（2）在Rt△OCD中，由勾股定理得OD==4（米）， …（7分）
∴BD=OD-OB=4-3=1（米）．
即梯子的底端向右滑1米. …（9分）
22.解：∵△ABC是等腰直角三角形，
∴AC=BC，∠ACB=90°，
∴∠ACD+∠BCE=90°.
∵∠ADC=90°，
∴∠ACD+∠DAC=90°，
∴∠DAC=∠BCE，
在△ADC和△CEB中，
，
∴△ADC≌△CEB（A.A.S），
∴DC=BE=12， …（5分）
∴AC2===169， …（7分）
∴该三角形零件的面积为AC·BC=AC2=84.5（cm2）． …（10分）
23.解：（1）如图，作过点A作AG⊥MN，垂足为G，
在Rt△ACD中，由勾股定理得，CD==400.
∵AC·AD=CD·AG，
∴AG=192（米），
∴A单元住户会受到影响． …（6分）

（2）如图，在MN上找到点S，T，使得AS=AT=200米
∴GT=GS==56.
∴ST=2GT=112. …（8分）
又∵速度V=252千米/小时=70（米/秒）
∴时间t=（112+228）÷70=（秒），
即受影响的时间为秒． …（12分）
24.（1）如图，在△ABC中，AB=15，BC=14，AC=13，
设BD=x，则CD=14-x，
在Rt△ABD中，由勾股定理得AD2=AB2-BD2=152-x2，
在Rt△ACD中，AD2=AC2-CD2=132-（14-x）2， …（4分）
∴152-x2=132-（14-x）2，
解得x=9．
∴AD=12． 
∴S△ABC=BC•AD=×14×12=84． …（7分）
（2）如图所示，△AP1C为直角三角形，且AC为直角边时，

在Rt△ADP1中，AP12=AD2+DP12=144+DP12，
在Rt△ACP1中，AP12=CP12-AC2=（DP1+5）2-169，
即144+DP12=（DP1+5）2-169，
解得P1D=，
此时CP1=. …（12分）
△AP2C为直角三角形，且AC为斜边时，易知此时P2与D重合时，此时，CP2=5.
综上，CP的长为  或5. …（14分）