高教版（中职）基础模块上册2.3 一元二次不等式完美版课件ppt

*揭示课题

3.1函数的概念及其表示法

*创设情景 兴趣导入

问题   

学校商店销售某种果汁饮料，售价每瓶2.5元，购买果汁饮料的瓶数与应付款之间具有什么关系呢？

解决

设购买果汁饮料瓶，应付款为，则计算购买果汁饮料应付款的算式为

                       ．

归纳

因为表示购买果汁饮料瓶数，所以可以取集合中的任意一个值，按照算式法则，应付款有唯一的值与之对应．

两个变量之间的这种对应关系叫做函数关系．

介绍

播放

课件

质疑

引导

分析

了解

观看

课件

思考

自我

分析

从实

际事

例使

学生

自然

的走

向知

识点

引导

启发

学生

体会

对应

5

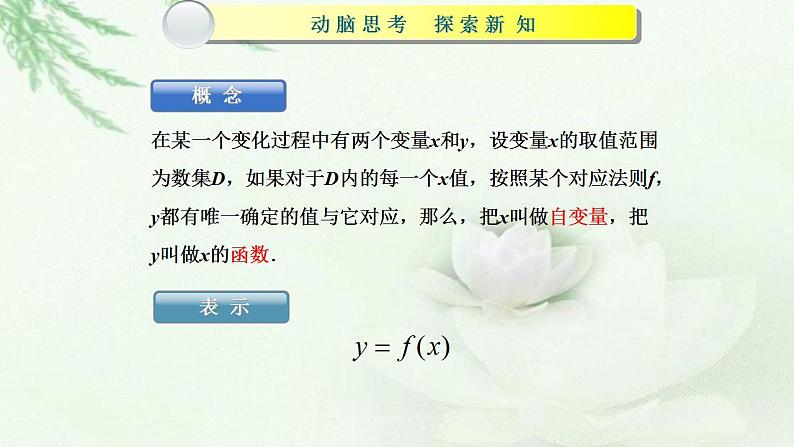
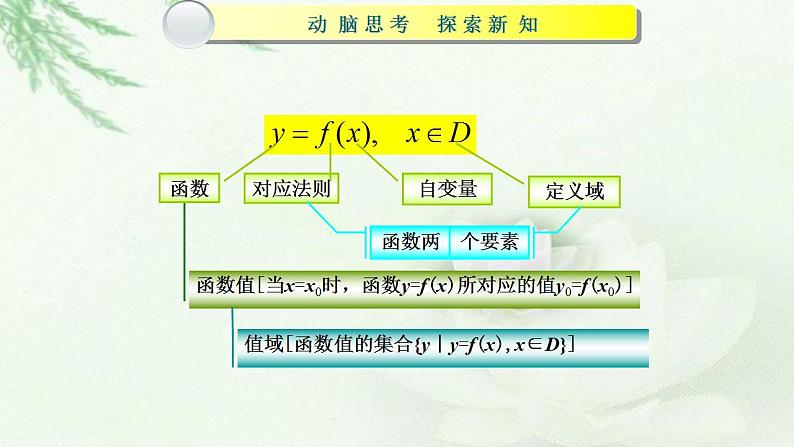
*动脑思考 探索新知

概念

在某一个变化过程中有两个变量x和y，设变量x的取值范围为数集D，如果对于D内的每一个x值，按照某个对应法则，都有唯一确定的值与它对应，那么，把叫做自变量，把叫做的函数．

表示

    将上述函数记作．

变量叫做自变量，数集D叫做函数的定义域．

当时，函数对应的值叫做函数在点处的函数值．记作.

函数值的集合叫做函数的值域．

函数的定义域与对应法则一旦确定，函数的值域也就确定了．因此函数的定义域与对应法则叫做函数的两个要素．

说明

定义域与对应法则都相同的函数视为同一个函数，而与选用的字母无关．如函数与表示的是同一个函数．

例如，函数的定义域为，函数的定义域为R．它们的定义域不同，因此不是同一个函数；函数与的定义域相同，都是R，但是它们的对应法则不同，因此不是同一个函数.

仔细

分析

讲解

关键

词语

强调

讲解

说明

思考

理解

记忆

观察

领会

了解

带领

学生

总结

上述

问题

得到

函数

概念

充分

讲解

函数

变量

和法

则之

间的

关系

10

*巩固知识 典型例题

例１　求下列函数的定义域：

（１）；　　　　（２）．

分析　如果函数的对应法则是用代数式表示的，那么函数的定义域就是使得这个代数式有意义的自变量的取值集合．

解　（１）由，得．

因此函数的定义域为，

用区间表示为．

（２）由，得．

因此函数的定义域为．

归纳　代数式中含有分式，使得代数式有意义的条件是分母不等于零；代数式中含有二次根式，使得代数式有意义的条件是被开方式大于或等于零．

例2  设，求，，，．

分析　本题是求自变量时对应的函数值，方法是将代入函数表达式求值．

解      ，

　　　　，

，

．

质疑

说明

引领

强调[来源:Z,xx,k.Com]

讲解

分析

讲解

观察

思考

主动

求解

记忆

观察

思考

理解

通过

例题

强化

定义

域的

含义

及时

归纳

定义

域的

基本

情况

[来源:学§科§网Z§X§X§K]

突出

代入

意义

注意

观察

学生

是否

理解

知识

点

25

*运用知识 强化练习  

教材练习3.1.1

1．求下列函数的定义域：

（1）；（2）．

2．已知，求，，．

3．判定下列各组函数是否为同一个函数：

（1）， ；（2），．

提问

巡视

指导

思考

动手

求解

交流

及时

了解

学生

知识

掌握

情况

35

*创设情景 兴趣导入

问题  观察下面的三个例子，分别用什么样的形式表示函数：

1.观察某城市2008年8月16日至8月25日的日最高气温统计表：

由表中可以清楚地看出日期和最高气温()之间的函数关系．

2. 某气象站用温度自动记录仪记录下来的2008年11月29日0时至14时的气温（）随时间（h）变化的曲线如下图所示：

曲线形象地反映出气温（）与时间（h）之间的函数关系，这里函数的定义域为．对定义域中的任意时间，有唯一的气温与之对应．例如，当时，气温；当时，气温．

3. 用S来表示半径为的圆的面积，则．这个公式清楚地反映了半径与圆的面积S之间的函数关系，这里函数的定义域为．以任意的正实数为半径的圆的面积为．

质疑

引导

分析

质疑

引导

分析

说明

说明

启发

引领

观察

思考

自我

体会

观察

思考

自我

体会

了解

体会

领悟

引导

启发

学生

了解

体会

函数

的三

种表

示方

法的

特点

从函

数的

角度

讲解

公式

45

*动脑思考 探索新知

函数的表示方法:常用的有列表法、图像法和解析法三种.

(1)列表法：就是列出表格来表示两个变量的函数关系.

例如，数学用表中的平方表、平方根表、三角函数表，银行里的利息表，列车时刻表等都是用列表法来表示函数关系的.

用列表法表示函数关系的优点：不需要计算就可以直接看出与自变量的值相对应的函数值.

(2)图像法：就是用函数图像表示两个变量之间的函数关系.

例如，我国人口出生率变化的曲线，工厂的生产图像，股市走向图等都是用图像法表示函数关系的.

用图像法表示函数关系的优点：能直观形象地表示出自变量的变化，相应的函数值变化的趋势.

(3)解析法：把两个变量的函数关系，用一个等式表示，这个等式叫做函数的解析表达式，简称解析式.

   例如，s=60t2，A=r2，S=2,y=(x2)等都是用解析式表示函数关系的.

用解析式表示函数关系的优点：一是简明、全面地概括了变量间的关系；二是可以通过解析式求出任意一个自变量的值所对应的函数值.

总结

归纳

介绍

说明

举例

说明

举例

介绍

思考

理解

记忆

观察

体会

了解

带领

学生

总结

函数

的三

种表

示方

法并

了解

其各

自的

特点

可以

教给

学生[来源:

自我

分析

总结

55

*巩固知识 典型例题

例4　文具店内出售某种铅笔，每支售价为0.12元，应付款额是购买铅笔数的函数，当购买6支以内（含6支）的铅笔时，请用三种方法表示这个函数．

分析　函数的定义域为{1，2，3，4，5，6}，分别根据三种函数表示法的要求表示函数．

解　设表示购买的铅笔数（支），表示应付款额（元），则函数的定义域为．

    （1）根据题意得，函数的解析式为，故函数的解析法表示为，．

（2）依照售价，分别计算出购买1~6支铅笔所需款额，列成表格，得到函数的列表法表示．

 （3）以上表中的x值为横坐标，对应的y值为纵坐标，在直角坐标系中依次作出点（1，0.12），（2，0.24），（3，0.36），（4，0.48），（5，0.6），（6，0.72），得到函数的图像法表示．

归纳

    由例4的解题过程可以归纳出“已知函数的解析式，作函数图像”的具体步骤：

（1）确定函数的定义域；

 （2）选取自变量x的若干值（一般选取某些代表性的值）计算出它们对应的函数值y，列出表格；

 （3）以表格中x值为横坐标，对应的y值为纵坐标，在直角坐标系中描出相应的点；

 （4）根据题意确定是否将描出的点联结成光滑的曲线．

 这种作函数图像的方法叫做描点法．

例5  利用“描点法”作出函数的图像，并判断点（25，5）是否为图像上的点 (求对应函数值时，精确到0.01) ．

解  （1）函数的定义域为．

（2）在定义域内取几个自然数，分别求出对应函数值，列表：

（3）以表中的x值为横坐标，对应的y值为纵坐标，在直角坐标系中依次作出点（）．由于，所以点是图像上的点．

（4）用光滑曲线联结这些点，得到函数图像.

软件链接

   演示利用几何画板软件作例5图像，方法详见现代信息技术应用3.

质疑

说明

强调

引领

[来源:学#科#网Z#X#X#K]

讲解

启发

分析

强调

归纳

总结

说明

启发

引导

强调

讲解

演示

观察

体会

思考

主动

求解

理解

领会

领会

理解

记忆

了解

思考

求解

理解

欣赏

通过

例题

进一

步领

会函

数三

种表

示方

法的

特点

突出

图像

的作

法

数形

结合

带领

学生

总结

归纳

函数

的图

像做

法特

别注

意步

骤性

和细

节

演示

过程

中提

醒学

生注

意作

图的

细节

产生

兴趣

跃跃

欲试

70

*运用知识 强化练习

教材练习3.1.2

1．判定点，是否在函数的图像上．

2．市场上土豆的价格是3.2元／kg ，应付款额y是购买土豆数量x的函数．请分别用解析法和图像法表示这个函数．

提问

巡视

指导

动手

求解

交流

及时

了解

学生

知识

掌握

情况

80

*归纳小结 强化思想

本次课学了哪些内容？重点和难点各是什么？

*自我反思 目标检测

本次课采用了怎样的学习方法？

你是如何进行学习的？

你的学习效果如何？

引导

提问

回忆

反思

培养

学生

反思

学习

过程

的能

力

85

*继续探索 活动探究

(1)读书部分： 教材章节3.1，学习与训练3.1；

(2)书面作业： 学习与训练3.1训练题；

(3)实践调查：举出函数的生活实例．

说明

记录

90