


2020-2021学年2.3 一元二次不等式评课ppt课件
展开定义:形如:ax2+bx+c >0 (≥0)或ax2+bx+c<0(≤0)的不等式(其中a≠0 ),叫做一元二次不等式。满足一元二次不等式的未知数的取值范围,叫做这个不等式的解集。
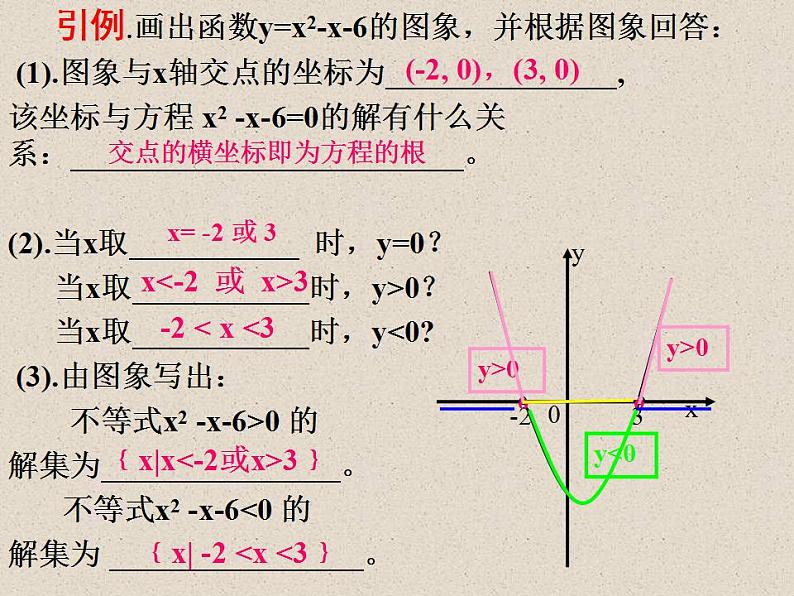
引例.画出函数y=x2-x-6的图象,并根据图象回答: (1).图象与x轴交点的坐标为 ,该坐标与方程 x2 -x-6=0的解有什么关系: 。 (2).当x取 时,y=0? 当x取 时,y>0? 当x取 时,y<0? (3).由图象写出: 不等式x2 -x-6>0 的解集为 。 不等式x2 -x-6<0 的解集为 。
(-2, 0),(3, 0)
交点的横坐标即为方程的根
x<-2 或 x>3
﹛x|x<-2或x>3﹜
﹛x| -2
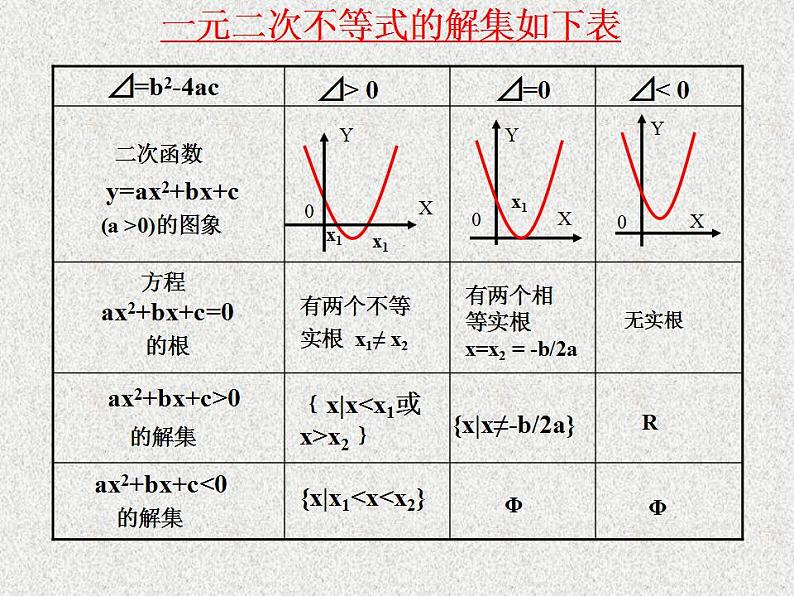
二次函数 y=ax2+bx+c (a >0)的图象
方程ax2+bx+c=0 的根
ax2+bx+c>0 的解集
ax2+bx+c<0 的解集
有两个不等实根 x1≠ x2
有两个相等实根x=x2 = -b/2a
﹛x|x
{x|x≠-b/2a}
{x|x1
解:∵ ⊿=b2-4ac= 22 +4× 15 > 0
方程x2-2x-15=0的两根为: x=-3,或x=5
∴ 不等式的解集为:{x│ x ≤-3 或x ≥5}。
解一元二次不等式的方法步骤是:
(3)根据图象写出解集
步骤:(1)化成标准形式 (a>0): ax2+bx+c>0 或 ax2+bx+c<0
(2)求⊿,解方程,画图象;
二、二次不等式的简单应用
解法1:(换元法) 设│x│ =t,则t ≥ 0原不等式可化为 t2 -2t-15≥0 由例1 可知解为t≥5或t≤-3 ∵t ≥ 0 ∴ 不等式的解集为{t│t≥5 } ∴ │x│≥5 ∴原不等式的解为{x│x≥5或x≤-5 }。
分析1:不同于x2-2x-15≥0的根本点在于不等式中含│x│,由于│x│ 2 = x2 ,则可以通过换元令│x│ =t,将不等式转化为t 2-2 t -15≥0求解。
x2-2 x -15≥0
x2-2│x│-15≥0
解法2:当x>0时, 原不等式可化为x2 -2x-15≥0 则不等式的解为x≥5或 x≤-3 ∵x>0 ∴ 不等式的解集为{x│x≥5 }
当x ≤0时, 原不等式可化为x2 +2x-15≥0 则不等式的解为x≥3或x ≤-5 ∵x≤0 ∴ 不等式的解集为{x│x≤-5 } 由以上可知原不等式的解为{x│x≥5或x≤-5 }。
分析2:也可用绝对值定义去掉绝对值将不等式转化为不含绝对值的求解。
例1 、解不等式: x2-2│x│-15≥0
例2 . 已知一元二次不等式a x2 +bx+6>0 的解集为{x │- 2 <x<3}, 求a-b的值.
解:由条件可知 : 方程a x2 +bx+6=0的根-2,3 又解在两根之间;
分析:二次不等式的解是通过二次方程的根来确定的,
∵ 6 /a = -2× 3= -6 ∴ a=-1 ∵ b /a = -2+3=1 ∴ b=1 则a-b=-2
由此可以理解为 a x2 +bx+6=0的根为-2,3。
另解:由条件可知 : 方程 a x2 +bx+6=0的根-2、3 , 代入方程可得:
2021学年第2章 不等式2.3 一元二次不等式一等奖ppt课件: 这是一份2021学年第2章 不等式2.3 一元二次不等式一等奖ppt课件,共21页。PPT课件主要包含了情境导入,探索新知,例题辨析,巩固练习,归纳总结,布置作业等内容,欢迎下载使用。
高中数学语文版(中职)基础模块上册2.3 一元二次不等式教学演示课件ppt: 这是一份高中数学语文版(中职)基础模块上册2.3 一元二次不等式教学演示课件ppt,共12页。PPT课件主要包含了教学目标,情境导入,探究新知,例题分析,检测反馈,总结提升,重点难点,课堂检测等内容,欢迎下载使用。
2021学年2.3 一元二次不等式课文课件ppt: 这是一份2021学年2.3 一元二次不等式课文课件ppt,共12页。PPT课件主要包含了教学目标,情境导入,探究新知,例题分析,检测反馈,总结提升,重点难点,课堂检测等内容,欢迎下载使用。












