






高中数学高教版(中职)拓展模块1.3.3 正弦定理与余弦定理应用举例教学ppt课件
展开我们知道,在直角三角形ABC(如图)中,
当三角形为钝角三角形时,不妨设角A为钝角,如图所示,以A为原
两边取与单位向量j的数量积,得
设与角A,B,C相对应的边长分别为a,b,c,故
当三角形为锐角三角形时,同样可以得到这个结论.于是得到
在三角形中,各边与它所对的角的正弦之比相等.
利用正弦定理可以求解下列问题:
(1)已知三角形的两个角和任意一边,求其他两边和一角.
(2)已知三角形的两边和其中一边所对角,求其他两角和一边.
三角形中任意一边的平方等于其余两边的平方和减去这两边与其
夹角余弦乘积的两倍. 即
公式(1.8)经变形后可以写成
利用余弦定理可以求解下列问题:
(1) 已知三角形的两条边和它们的夹角,求第三边和其他的
(2) 已知三角形的三边,求三个角.
分析 这是已知三角形的两条边和它们的夹角,求第三边的
问题,可以直接应用余弦定理.
解 由于a<b<c,所以C最大,A最小,
由公式(1.9),有
正弦定理、余弦定理的内容:
在△ABC中,a=20,b=29,c=21,求角B.
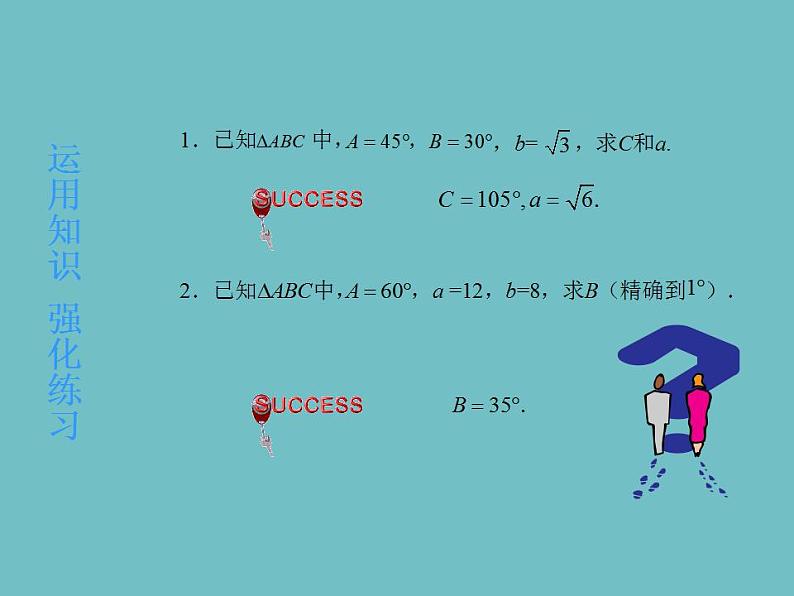
高中高教版(中职)1.3.1 正弦定理优质ppt课件: 这是一份高中高教版(中职)1.3.1 正弦定理优质ppt课件,共10页。PPT课件主要包含了创设情境兴趣导入,巩固知识典型例题,由正弦定理得,运用知识强化练习,理论升华整体建构,自我反思目标检测等内容,欢迎下载使用。
语文版(中职)拓展模块1.3 正弦定理、余弦定理备课课件ppt: 这是一份语文版(中职)拓展模块1.3 正弦定理、余弦定理备课课件ppt,共18页。PPT课件主要包含了创设情境兴趣导入,动脑思考探索新知,正弦定理,巩固知识典型例题,运用知识强化练习,余弦定理,两个角,理论升华整体建构,自我反思目标检测等内容,欢迎下载使用。
数学1.2 余弦定理、正弦定理集体备课课件ppt: 这是一份数学1.2 余弦定理、正弦定理集体备课课件ppt,共37页。PPT课件主要包含了不难得到,正弦定理,同理可得,此时有,证法1,交BC延长线于D,过点A作AD⊥BC,作外接圆O,向量法,证法2等内容,欢迎下载使用。












