初中数学人教版九年级上册第二十二章 二次函数综合与测试优秀练习题

     人教版九年级数学（上）单元目标分层提分试卷（八）

  （测试范围： 第22章《二次函数》全章综合测试   时间：100分钟 总分值：120分）

一、选择题（每题3分，共24分）

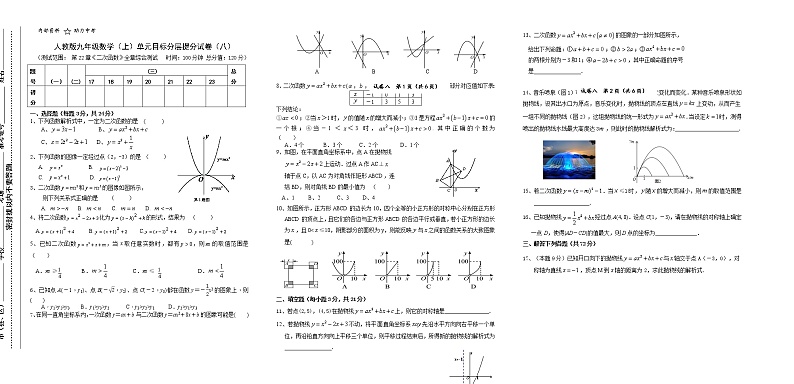
1、下列函数解析式中，一定为二次函数的是  (  　　)

A、        B、 

  C、  D、

2、下列函数的图像一定经过点（2，-3）的是 （     ）

   A.           B.      

C.         D.

3、二次函数和的图像如图所示，

则下列关系式正确的是    （     ）

A.   B.    C.    D.

4、将二次函数化为的形式，结果为  （     ）

A.     B.    C.    D.

5、已知二次函数，当取任意实数时，都有，则的取值范围是（    ）

A．≥       B．         C．≤              D．

6、已知点A(－1，y1)、点B(－，y2)、点C(－2，y3)都在函数y＝－x2的图象上，则(    )

A．y1>y2>y3    B．y1>y3>y2      C．y3>y2>y1     D．y2>y1>y3

7、在同一直角坐标系内，一次函数y＝ax＋b与二次函数y＝ax2＋8x＋b的图象可能是(　　)

A                   B                  C                D

8、二次函数(，，为常数，且≠0)中的与的部分对应值如下表：

下列结论：

①；②当＞1时，的值随的增大而减小；③3是方程的一个根；④当－1＜＜3时，.其中正确的个数为          （    ）                                        

A．4个       B．3个      C．2个        D．1个

9、如图，在平面直角坐标系中，点A在抛物线

上运动．过点A作AC⊥

轴于点C，以AC为对角线作矩形ABCD，连

结BD，则对角线BD的最小值为  （    ）

A、1     B、2      C、3     D、4

10、如图所示，正方形ABCD的边长为10，四个全等的小正方形的对称中心分别在正方形ABCD的顶点上，且它们的各边与正方形ABCD的各边平行或垂直，若小正方形的边长为，且0<≤10，阴影部分的面积为y，则能反映与之间的函数关系的大致图象是(       )

二、填空题（每小题3分，共21分）

11、若点(2,5)，(4,5)在抛物线上，则它的对称轴是________________.

12、若抛物线不动，将平面直角坐标系先沿水平方向向右平移一个单位，再沿铅直方向向上平移三个单位，则平移过程结束后，所得新的抛物线的解析式为_________________.

13、二次函数的图象的一部分如图所示，

给出下列命题：①；②；③

的两根分别为－3和1；④，其中正确命题的序号

是_________________.

14、音乐喷泉（图1）可以使喷水造型随音乐的节奏起伏变化而变化．某种音乐喷泉形状如抛物线，设其出水口为原点，音乐变化时，抛物线的顶点在直线上变动，从而产生一组不同的抛物线（图2），这组抛物线的统一形式为.当设定时，测得喷出的抛物线水线最大高度达3，则此时的抛物线解析式为：_______________________.

15、若二次函数．当≤l时，随的增大而减小，则的取值范围是____________________.

16、已知抛物线经过点A(4,0)．设点C(1，－3)，请在抛物线的对称轴上确定一点D，使得|AD－CD|的值最大，则D点的坐标为_______________．

三、解答下列各题（共72分）

18、（本题10分）已知抛物线，其中是常数.

（1）求证：不论为何值，该抛物线与轴一定有两个公共点.

（2）把抛物线沿轴向上平移多少个单位长度后，得到的抛物线与轴只有一个公共点？

19、（本题10分）如图，抛物线与轴交于A、B两点（点A在点B左边），与轴交于点C，且AB＝4.

   （1）求抛物线的解析式；

（2）过点C作CD⊥AC，且CD＝AC，AD交抛物线于点P，求点P的坐标.

20.（本题10分）如图，一位运动员在距篮下4米处跳起投篮，球运行的路线是抛物线，当球运行的水平距离为2.5米时，达到最大高度3.5米，然后准确落入篮圈。已知篮圈中心到地面的距离为3.05米.

 (1)建立如图所示的直角坐标系，求抛物线的表达式；

(2)该运动员身高1.8米，在这次跳投中，球在头顶上方0.25米处出手，问：球出手时，他跳离地面的高度是多少？

（1）设该品牌商品涨价后的定价为每件元，则每星期的销售量为_____________件.

22、（本题11分）如图1，P（m，n）是抛物线上任意一点，是过点（0，﹣2）且与轴平行的直线，过点P作直线PH⊥，垂足为H．

【探究】

（1）          填空：当=0时，OP=______，PH=________；

当=4时，OP=______，PH=______；

【证明】

（2）          对任意，，猜想OP与PH的大小关系，

并证明你的猜想．

【应用】

（3）如图2，已知线段AB=6，端点A，B在抛物线

上滑动，那么A，B两点到直线的

距离之和的最小值____________．

23、（本题11分）如图，抛物线与

轴交于A、B两点，与轴交于点C，抛物线的对称

轴交轴于点D，已知A（－1，0），C（0，2）.

（1）求抛物线的解析式；

（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，求出点P的坐标；如果不存在，请说明理由.