人教版八年级上册13.4课题学习 最短路径问题教学ppt课件

这是一份人教版八年级上册13.4课题学习 最短路径问题教学ppt课件，共13页。PPT课件主要包含了垂线段最短，两点之间线段最短，你学会了吗，探究二将军饮马问题，知识点，思想与方法，转化的思想，最短路径问题，梳理与感悟，拓展延伸等内容，欢迎下载使用。
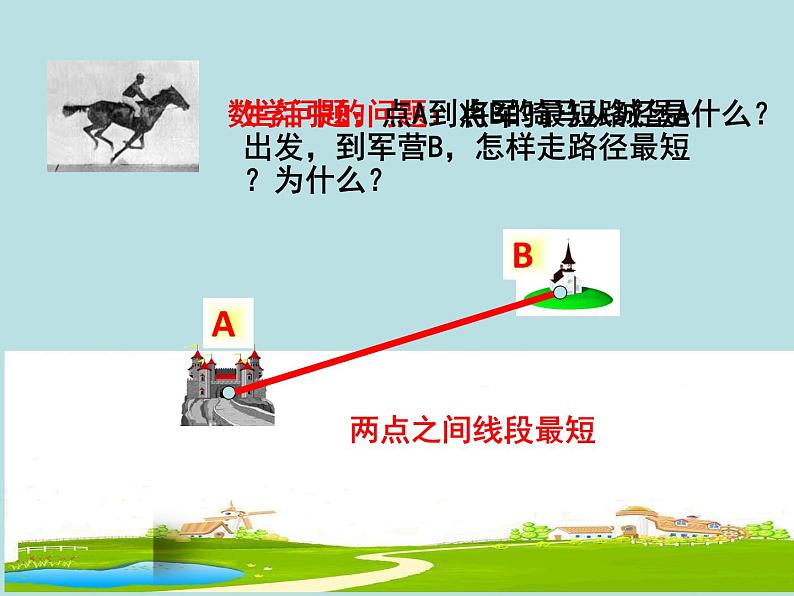
生活中的问题：将军骑马从城堡A出发，到军营B，怎样走路径最短？为什么？
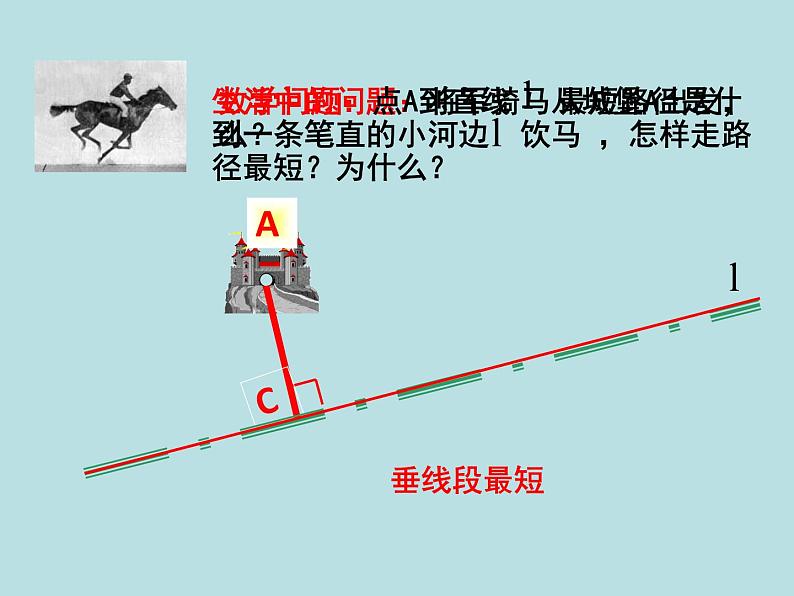
数学问题：点A到点B的最短路径是什么？

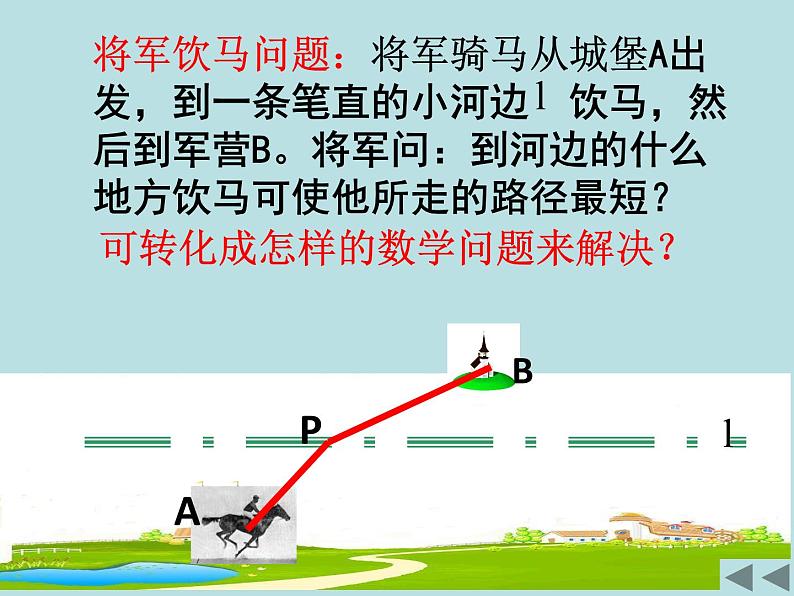
将军饮马问题：将军骑马从城堡A出发，到一条笔直的小河边 饮马，然后到军营B。将军问：到河边的什么地方饮马可使他所走的路径最短？
可转化成怎样的数学问题来解决？
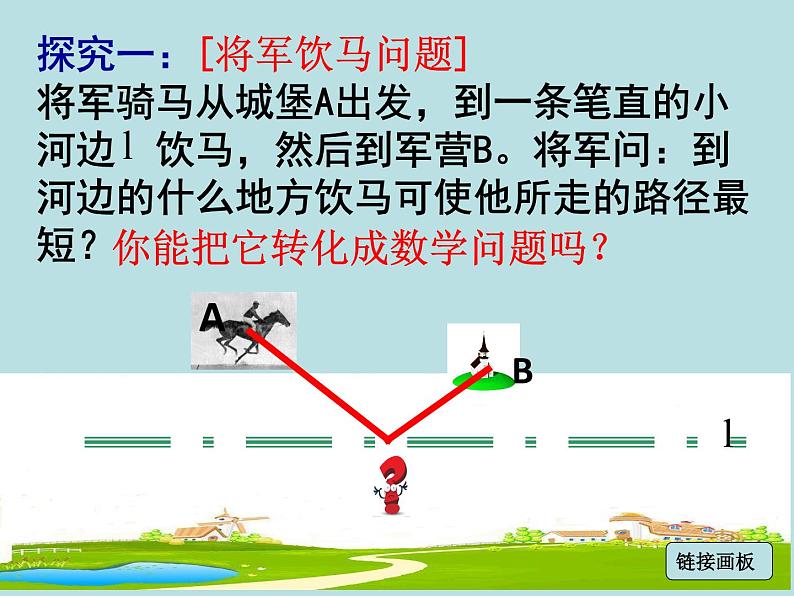
探究一：[将军饮马问题]将军骑马从城堡A出发，到一条笔直的小河边 饮马，然后到军营B。将军问：到河边的什么地方饮马可使他所走的路径最短？
你能把它转化成数学问题吗？
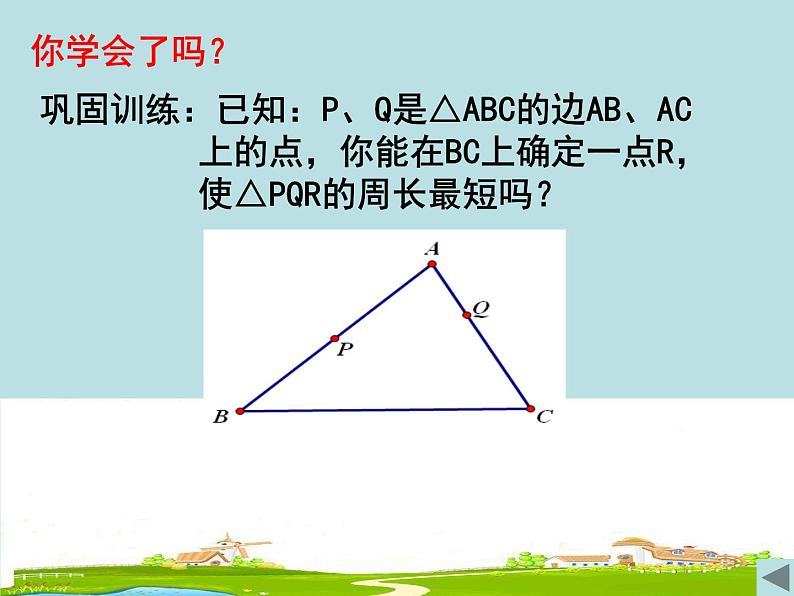
巩固训练：已知：P、Q是△ABC的边AB、AC 上的点，你能在BC上确定一点R， 使△PQR的周长最短吗？
如图：一位将军骑马从城堡A出发，先骑马去草地边OM的某处吃草，再骑马去河边ON喝水，最后回到城堡A， 问：这位将军怎样走路程最短？
数学问题：在射线OM、ON上分别找一点P、Q，使AP+PQ+QA最短
探究三： 已知P是∠BAC的边AB上的点， 你能在AB、AC上分别确定一点Q和R， 使 PQ+PR 最短吗？
最短路径问题的几种模式
两点之间线段最短/垂线段最短
方法：作轴对称
变式一：背景为等腰三角形
如图,已知在等腰△ABC 中, ∠ABC=120,P是底边AC上的一个动点, M、N分别是AB、BC的中点,若PM+PN的最小值为2，求△ ABC的周长.
变式二：背景为长方形、正方形
如图所示，四边形OABC为正方形，边长为3，点A，C分别在x轴，y轴的正半轴上，点D在OA上，且D的坐标为（1，0），P是OB上的一动点，则“求PD+PA和的最小值”要用到的数理依据是（ ）