2022届高考数学一轮复习第八章平面解析几何8.6抛物线学案理含解析北师大版

这是一份2022届高考数学一轮复习第八章平面解析几何8.6抛物线学案理含解析北师大版，共12页。

第六节　抛物线
命题分析预测
学科核心素养
从近五年的考查情况来看，抛物线的定义、标准方程、几何性质以及直线与抛物线的位置关系是高考的命题热点，常以选择题和填空题的形式出现，直线与抛物线的位置关系常以解答题的形式出现．
本节主要考查考生的转化与化归思想的运用，提升考生数学运算、直观想象核心素养．

授课提示：对应学生用书第181页
知识点一　抛物线的定义
满足以下三个条件的点的轨迹是抛物线：
（1）在平面内；
（2）动点到定点F的距离与到定直线l的距离相等；
（3）定点不在定直线上．
• 温馨提醒 •
抛物线的定义中易忽视“定点不在定直线上”这一条件，当定点在定直线上时，动点的轨迹是过定点且与直线垂直的直线．

1．抛物线y2＝8x上到其焦点F距离为5的点P有（　　）
A．0个　　　　　　 B．1个
C．2个 D．4个
解析：设P（x1，y1），则|PF|＝x1＋2＝5，y＝8x1，所以x1＝3，y1＝±2．故满足条件的点P有两个．
答案：C
2．（易错题）设抛物线y2＝8x上一点P到y轴的距离是4，则点P到该抛物线焦点的距离是_________．
解析：抛物线y2＝8x的准线方程x＝－2，因为点P到y轴的距离为4，所以点P到准线的距离为6，由抛物线定义知点P到焦点的距离为6．
答案：6
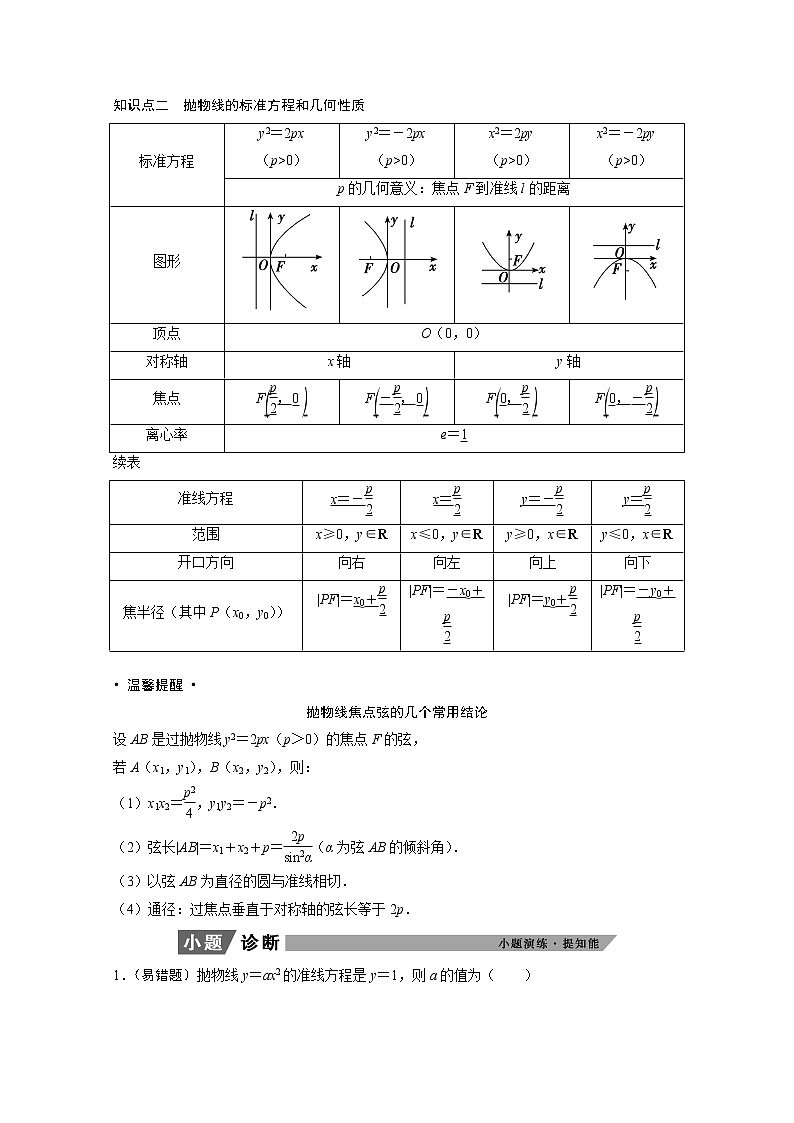
知识点二　抛物线的标准方程和几何性质
标准方程
y2＝2px
（p>0）
y2＝－2px
（p>0）
x2＝2py
（p>0）
x2＝－2py
（p>0）
p的几何意义：焦点F到准线l的距离
图形




顶点
O（0，0）
对称轴
x轴
y轴
焦点
F
F
F
F
离心率
e＝1
续表
准线方程
x＝－
x＝
y＝－
y＝
范围
x≥0，y∈R
x≤0，y∈R
y≥0，x∈R
y≤0，x∈R
开口方向
向右
向左
向上
向下
焦半径（其中P（x0，y0））
|PF|＝x0＋
|PF|＝－x0＋
|PF|＝y0＋
|PF|＝－y0＋

• 温馨提醒 •
抛物线焦点弦的几个常用结论
设AB是过抛物线y2＝2px（p＞0）的焦点F的弦，
若A（x1，y1），B（x2，y2），则：
（1）x1x2＝，y1y2＝－p2．
（2）弦长|AB|＝x1＋x2＋p＝（α为弦AB的倾斜角）．
（3）以弦AB为直径的圆与准线相切．
（4）通径：过焦点垂直于对称轴的弦长等于2p．

1．（易错题）抛物线y＝ax2的准线方程是y＝1，则a的值为（　　）
A． B．－
C．4 D．－4
解析：由题意知抛物线的标准方程为x2＝y，所以准线方程y＝－＝1，解得a＝－．
答案：B
2．过点P（－2，3）的抛物线的标准方程是（　　）
A．y2＝－x或x2＝y
B．y2＝x或x2＝y
C．y2＝x或x2＝－y
D．y2＝－x或x2＝－y
解析：设抛物线的标准方程为y2＝kx或x2＝my，代入点P（－2，3），解得k＝－，m＝，所以y2＝－x或x2＝y．
答案：A
3．过抛物线y2＝4x的焦点的直线l交抛物线于P（x1，y1），Q（x2，y2）两点，如果x1＋x2＝6，则|PQ|＝_________．
解析：抛物线y2＝4x的焦点为F（1，0），准线方程为x＝－1．根据题意可得，|PQ|＝|PF|＋|QF|＝x1＋1＋x2＋1＝x1＋x2＋2＝8．
答案：8

授课提示：对应学生用书第182页
题型一　抛物线的标准方程及几何性质　　
1．（2021·宜春联考）已知抛物线C：y2＝2px（p＞0）的焦点为F，点M是抛物线C上一点，圆M与y轴相切，且被直线x＝截得的弦长为p，若|MF|＝，则抛物线的方程为（　　）
A．y2＝4x　　　　　　　 B．y2＝2x
C．y2＝8x D．y2＝x
解析：设圆M与y轴相切于点N，直线x＝与圆M交于A，B两点，如图所示，设M（x0，y0），则|MN|＝|MA|＝|MB|＝x0，|AB|＝p，所以＋＝x，解得x0＝p，由抛物线的定义知，|MF|＝x0＋，因为|MF|＝，所以＝p＋p，即p＝2，所以抛物线方程为y2＝4x．

答案：A
2．已知抛物线C：y2＝8x的焦点为F，准线为l，P是l上一点，Q是直线PF与C的一个交点，若＝4，则|QF|＝（　　）
A． B．
C．3 D．2
解析：因为＝4，所以＝．如图，过Q作QQ′⊥l，垂足为Q′，设l与x轴的交点为A，则|AF|＝4，所以＝＝．所以|QQ′|＝3，根据抛物线定义可知|QQ′|＝|QF|＝3．

答案：C
3．（2021·辽宁五校联考）抛物线C：y2＝4x的焦点为F，N为准线上一点，M为y轴上一点，∠MNF为直角，若线段MF的中点E在抛物线C上，则△MNF的面积为（　　）
A． B．
C． D．3
解析：如图所示，不妨设点N在第二象限，连接EN，易知F（1，0），因为∠MNF为直角，点E为线段MF的中点，所以|EM|＝|EF|＝|EN|，又E在抛物线C上，所以EN⊥l，E，所以N（－1，），M（0，2），所以|NF|＝，|NM|＝，所以△MNF的面积为．

答案：C
4．（2020·高考全国卷Ⅲ）设O为坐标原点，直线x＝2与抛物线C：y2＝2px（p＞0）交于D，E两点，若OD⊥OE，则C的焦点坐标为（　　）
A． B．
C．（1，0） D．（2，0）
解析：法一：∵抛物线C关于x轴对称，∴D，E两点关于x轴对称．可得出直线x＝2与抛物线的两交点的坐标分别为（2，2），（2，－2）．不妨设D（2，2），E（2，－2），则＝（2，2），＝（2，－2）．又∵OD⊥OE，∴·＝4－4p＝0，解得p＝1，∴C的焦点坐标为．
法二：∵抛物线C关于x轴对称，∴D，E两点关于x轴对称．∵OD⊥OE，∴D，E两点横、纵坐标的绝对值相等．不妨设点D（2，2），将点D的坐标代入C：y2＝2px，得4＝4p，解得p＝1，故C的焦点坐标为．
答案：B

1．求抛物线方程的三个注意点
（1）当坐标系已建立时，应根据条件确定抛物线方程属于四种类型中的哪一种．
（2）要注意把握抛物线的顶点、对称轴、开口方向与方程之间的对应关系．
（3）要注意参数p的几何意义是焦点到准线的距离，利用它的几何意义来解决问题．
2．运用抛物线几何性质的技巧
涉及抛物线几何性质的问题常结合图形思考，通过图形可以直观地看出抛物线的顶点、对称轴、开口方向等几何特征，体现了数形结合思想解题的直观性．
题型二　抛物线的定义及应用　　
　　与抛物线定义相关的最值问题常涉及距离最短、距离和最小等等．常见的命题角度有：（1）焦点与定点距离之和最小问题；（2）点与准线的距离之和最小问题；（3）焦点弦中距离之和最小问题．
考法（一）　焦点与定点距离之和最小问题
[例1]　（2021·赣州模拟）若点A的坐标为（3，2），F是抛物线y2＝2x的焦点，点M在抛物线上移动时，使|MF|＋|MA|取得最小值的M的坐标为（　　）
A．（0，0）　　　　　　 B．
C．（1，） D．（2，2）
[解析]　过M点作准线的垂线，垂足是N（图略），则|MF|＋|MA|＝|MN|＋|MA|，当A，M，N三点共线时，|MF|＋|MA|取得最小值，此时M（2，2）．
[答案]　D
考法（二）　点与准线的距离之和最小问题
[例2]　（2021·邢台摸底）已知M是抛物线x2＝4y上一点，F为其焦点，点A在圆C：（x＋1）2＋（y－5）2＝1上，则|MA|＋|MF|的最小值是_________．
[解析]　依题意，由点M向抛物线x2＝4y的准线l：y＝－1引垂线，垂足为M1（图略），则有|MA|＋|MF|＝|MA|＋|MM1|，结合图形可知|MA|＋|MM1|的最小值等于圆心C（－1，5）到y＝－1的距离再减去圆C的半径，即等于6－1＝5，因此|MA|＋|MF|的最小值是5．
[答案]　5
考法（三）　焦点弦中距离之和最小问题
[例3]　已知抛物线y2＝4x，过焦点F的直线与抛物线交于A，B两点，过A，B分别作y轴垂线，垂足分别为C，D，则|AC|＋|BD|的最小值为_________．
[解析]　由题意知F（1，0），|AC|＋|BD|＝|AF|＋|FB|－2＝|AB|－2，即|AC|＋|BD|取得最小值时当且仅当|AB|取得最小值，依抛物线定义知当|AB|为通径，即|AB|＝2p＝4时为最小值，所以|AC|＋|BD|的最小值为2．
[答案]　2

与抛物线有关的最值问题的两个转化策略
（1）将抛物线上的点到准线的距离转化为该点到焦点的距离，构造出“两点之间线段最短”，使问题得解．
（2）将抛物线上的点到焦点的距离转化为到准线的距离，利用“与直线上所有点的连线中垂线段最短”原理解决．
[题组突破]
1．已知直线l1：4x－3y＋6＝0和直线l2：x＝－1，则抛物线y2＝4x上一动点P到直线l1和直线l2的距离之和的最小值是_________．
解析：由题可知l2：x＝－1是抛物线y2＝4x的准线，设抛物线的焦点F为（1，0），则动点P到l2的距离等于|PF|，则动点P到直线l1和直线l2的距离之和的最小值即为焦点F到直线l1：4x－3y＋6＝0的距离，所以最小值是＝2．
答案：2
2．（2021·上海虹口区模拟）已知点M（20，40），抛物线y2＝2px（p＞0）的焦点为F．若对于抛物线上的任意点P，|PM|＋|PF|的最小值为41，则p的值等于_________．
解析：过点P作抛物线准线的垂线，垂足为D，则|PF|＝|PD|．根据点M与抛物线的位置分类讨论，当点M（20，40）位于抛物线内时，
如图（1），|PM|＋|PF|＝|PM|＋|PD|．
当点M，P，D共线时，|PM|＋|PF|的值最小．
由最小值为41，得20＋＝41，解得p＝42．
当点M（20，40）位于抛物线外时，如图（2），当点P，M，F共线时，|PM|＋|PF|的值最小．
由最小值为41，得 ＝41，解得p＝22或58．
当p＝58时，y2＝116x，点M（20，40）在抛物线内，故舍去．
综上，p＝42或22．

答案：42或22
题型三　直线与抛物线的位置关系　　
[例]　（2019·高考全国卷Ⅲ）已知曲线C：y＝，D为直线y＝－上的动点，过D作C的两条切线，切点分别为A，B．
（1）证明：直线AB过定点；
（2）若以E为圆心的圆与直线AB相切，且切点为线段AB的中点，求四边形ADBE的面积．
[解析]　（1）证明：设D，A（x1，y1），
则x＝2y1．
因为y′＝x，所以切线DA的斜率为x1，故＝x1．
整理得2tx1－2y1＋1＝0．
设B（x2，y2），同理可得2tx2－2y2＋1＝0．
故直线AB的方程为2tx－2y＋1＝0．
所以直线AB过定点．
（2）由（1）得直线AB的方程为y＝tx＋．
由可得x2－2tx－1＝0．
于是x1＋x2＝2t，x1x2＝－1，
y1＋y2＝t（x1＋x2）＋1＝2t2＋1，
|AB|＝|x1－x2|＝× ＝2（t2＋1）．
设d1，d2分别为点D，E到直线AB的距离，
则d1＝，d2＝．
因此，四边形ADBE的面积
S＝|AB|（d1＋d2）＝（t2＋3）．
设M为线段AB的中点，则M．
因为⊥，而＝（t，t2－2），与向量（1，t）平行，
所以t＋（t2－2）t＝0，解得t＝0或t＝±1．
当t＝0时，S＝3；当t＝±1时，S＝4．
因此，四边形ADBE的面积为3或4．

直线与抛物线相交问题处理规律
（1）凡涉及抛物线的弦长、弦的中点、弦的斜率问题时都要注意利用根与系数的关系，避免求交点坐标的复杂运算．解决焦点弦问题时，抛物线的定义有广泛的应用，而且还应注意焦点弦的几何性质．
（2）对于直线与抛物线相交、相切、中点弦、焦点弦问题，以及定值、存在性问题的处理，最好是作出草图，由图像结合几何性质做出解答．并注意“设而不求”“整体代入”“点差法”的灵活应用．
（3）对于抛物线x2＝2py的切线问题，常结合导数的几何意义求解切线的斜率．由y＝得k＝y′＝．
[对点训练]
设A，B为曲线C：y＝上两点，A与B的横坐标之和为4．
（1）求直线AB的斜率；
（2）设M为曲线C上一点，C在M处的切线与直线AB平行，且AM⊥BM，求直线AB的方程．
解析：（1）设A（x1，y1），B（x2，y2），
则x1≠x2，y1＝，y2＝，x1＋x2＝4，
于是直线AB的斜率k＝＝＝1．
（2）由y＝，得y′＝．设M（x3，y3），由题设知＝1，解得x3＝2，于是M（2，1）．设直线AB的方程为y＝x＋m，故线段AB的中点为N（2，2＋m），|MN|＝|m＋1|．将y＝x＋m代入y＝得x2－4x－4m＝0．当Δ＝16（m＋1）＞0，即m＞－1时，x1，2＝2±2．从而|AB|＝|x1－x2|＝4．由题设知|AB|＝2|MN|，即4＝2（m＋1），解得m＝7．所以直线AB的方程为y＝x＋7．
　抛物线几何性质应用中的核心素养
直观想象——抛物线几何性质的创新应用
[例]　（2021·合肥调研）设抛物线C：y2＝2px（p＞0）的焦点为F，斜率为k的直线过F交C于点A，B，＝2，则直线AB的斜率为（　　）
A．2　　　　　　 B．2
C．±2 D．±2
[解析]　法一：由题意知k≠0，F，则直线AB的方程为y＝k，代入抛物线方程消去x，得y2－y－p2＝0．不妨设A（x1，y1）（x1＞0，y1＞0），B（x2，y2），因为＝2，所以y1＝－2y2．又y1y2＝－p2，所以y2＝－p，x2＝，所以kAB＝＝2．根据对称性可得直线AB的斜率为±2．
法二：如图，过A，B分别作准线的垂线，垂足分别为D，E，设直线AB交准线于M，由抛物线的定义知|AF|＝|AD|，|BF|＝|BE|，结合＝2，知|BE|＝|AD|＝|AB|，则BE为△AMD的中位线，所以|AB|＝|BM|，所以|BE|＝|BM|，所以|ME|＝＝2|BE|，所以tan∠MBE＝＝2，即此时直线AB的斜率为2，根据对称性可得直线AB的斜率为±2．

[答案]　C

求解此类问题有两种方法：一是利用条件坐标化解决，注意几何性质的运用；二是数形结合充分利用平面几何性质，结合定义转化求解，注意向量的工具作用．
[对点训练]
（2021·惠州调研）已知F是抛物线C：y＝2x2的焦点，N是x轴上一点，线段FN与抛物线C相交于点M，若2＝，则|FN|＝（　　）
A．　　　　　 B．
C． D．1
解析：法一：因为抛物线C：y＝2x2，所以F，抛物线C的准线方程为y＝－．如图，过点M作抛物线准线的垂线，交x轴于点A，交抛物线C的准线于点B，则MA∥OF，所以＝．因为2＝，所以|MA|＝×＝，|MF|＝|MB|＝＋＝，|FN|＝3|FM|＝．

法二：因为抛物线y＝2x2，所以F．设N（x0，0），则由2＝，可得M，代入抛物线方程，得＝2，解得x＝，则|FN|＝＝ ＝．
答案：A