2020-2021学年河南省许昌市高一（下）6月月考数学试卷人教A版

这是一份2020-2021学年河南省许昌市高一（下）6月月考数学试卷人教A版，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 378∘化成弧度为( )
A.21π10B.21π20C.11π10D.11π5

2. 如果角α的终边过点−3,2，则( )
A.sinα=277B.csα=217C.tanα=233D.tanα=−32

3. 下列说法正确的是( )
A.若|a→|=|b→|，则a→与b→为相等向量
B.若a→与b→方向相反，则a→与b→为相反向量
C.若AB→=DC→，则A，B，C，D四点一定可以构成平行四边形
D.两个单位向量之和可能仍然是单位向量

4. 已知sinα=45，且π2<α<π，则csπ−α+2sinπ2+α=( )
A.35B.−35C.15D.95

5. 某同学从6岁到12岁的年龄与身高的折线图如图所示，根据折线图，下列说法正确的是( )

A.9岁到10岁的身高增长速度最快
B.从6岁到12岁，每年身高平均增长了5cm
C.从6岁到12岁，身高和年龄呈负相关
D.9岁到12岁比6岁到9岁的身高增长速度更快

6. 已知e1，e2是两个不共线的向量，OA→=e1→，OB→=ne2→，OC→=14e1→+e2→，若A，B，C三点共线，则n=( )
A.12B.13C.14D.34

7. 赵爽为《周髀算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”，它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形．如图所示的是一张弦图，直角三角形的三边长分别为3，4，5，若在大正方形内随机取一点，则这一点落在小正方形内的概率为( )

A.14B.19C.116D.125

8. 已知函数fx=2sin2x−π3，则( )
A.fx=−f−xB.fπ2+x=fx
C.fx−π6=f−xD.fπ6+x+f−x=0

9. 下图是用来计算2+2×5+2×52+2×53+2×54+2×55的一个程序框图，则判断框内应填入的条件是( )

A.i>4?B.i>5？C.i>6？D.i>7？

10. 如图，在△ABC中，D为线段BC上靠近B的三等分点，E为线段AC上靠近A的三等分点．若AB→=λAD→+μBE→，则λ+μ=( )

A.0B.13C.35D.65

11. 已知函数fx=tanx+|tanx|．现给出下列4个结论：
①fx的最小正周期为π2；
②点−π2,0是fx图象的一个对称中心；
③fx的值域为[0,+∞)；
④不等式fx>2的解集为π4+kπ,π2+kπk∈Z；
其中所有正确结论的序号是( )
A.①②B.③④C.①③D.②④

12. 将函数gx=3csπx−π3的图象向左平移16个单位长度，再向下平移1个单位长度后得到函数fx的图象．若fx的定义域为−3,3，则fx所有的零点之和等于( )
A.13B.1C.73D.143
二、填空题

已知一组数据的标准差是7.2，若将这组数据中的每一个数据都加上1，得到一组新的数据，则这组新数据的标准差为________．

已知向量a→与b→的夹角为π3，且|b→|=2，b→⋅a→+b→=6，则|a→|=________．

如图，在菱形ABCD中，AB=1，∠DAB=60∘，点E为BC边上的中点，则AC→⋅DE→=________．


已知函数fx=sin2x+π6+a，对任意的x1，x2，x3∈0,π12，fx1+fx2≥fx3恒成立，则a的取值范围为________．
三、解答题

已知向量a→=1,2，b→=x,−1．
(1)若a→⊥b→，求|a→+b→|．

(2)若a→//b→，求a→−b→⋅a→的值．

已知sinα+4csα2sinα−csα=2．
(1)求tanπ−α的值．

(2)求2sin2α−cs2α的值．

疫情后，居民减少了乘坐公共交通工具的频率，于是私家车销量提升了．现对某大型连锁汽车销售店的100名销售人员去年下半年的销售量进行统计，将数据按照90,110，(110,130]，(130,150]，(150,170]分成4组，得到如图所示的频率分布直方图．

(1)求这100名销售人员去年下半年销售量的平均数．（同一组中的每个数据可用该组区间的中点值代替）

(2)汽车销售店准备从去年下半年销售量在(130,150]，(150,170]之间的销售人员中，用分层抽样的方法抽取5名销售人员进行经验交流分享，并从这5人中任意抽取2人派到其他店巡回分享经验，求这2人不是来自同一组的概率．

在△ABC中，AC=2AB=2，∠BAC=90∘，CD→=λCA→．

(1)若BD→与BC→的夹角为π4，求λ的值．

(2)求BD→⋅CD→的最小值．

国家品牌计划是央视对过去广告的招标模式实现的一次创新，为入选企业定制宣传片及企业品牌故事，在央视各频道高频次播出，希望能提升企业品牌形象，以品牌建设驱动产业升级．现根据某家电企业近5年每年的广告费用x（单位：千万元）与销售额y（单位：千万元）的数据，得到如下统计表：

(1)根据所给的5组数据，求出y关于x的线性回归方程．

(2)该家电企业结合其他数据发现该回归方程只适用于广告费用不超过10千万元的情况，当超过10千万元时，销售额y与广告费用x的关系式满足y=−1000x+245，且该企业的生产成本占销售额的60%，为使企业获得最大利润，应投入多少广告费？（利润=销售额−广告费用−生产成本）
附：回归直线的斜率和截距的最小二乘估计公式分别为b=i=1n(xi−x¯)(yi−y¯)i=1n(xi−x¯)2=i=1nxiyi−nx¯⋅y¯i=1nxi2−nx¯2，
a=y¯−bx¯.

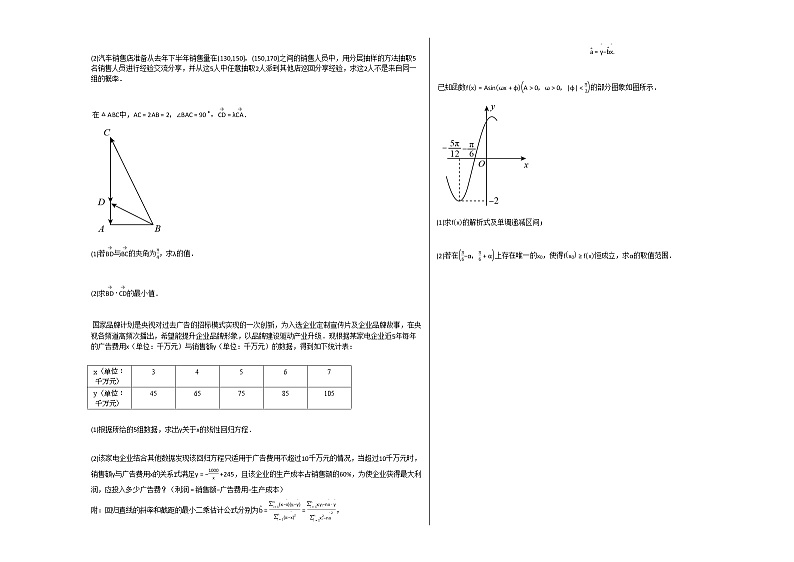
已知函数fx=Asinωx+φA>0，ω>0，|φ|<π2的部分图象如图所示．

(1)求fx的解析式及单调递减区间；

(2)若在π6−α，π6+α上存在唯一的x0，使得fx0≥fx恒成立，求α的取值范围．
参考答案与试题解析
2020-2021学年河南省许昌市高一（下）6月月考数学试卷
一、选择题
1.
【答案】
A
【考点】
弧度与角度的互化
【解析】
无
【解答】
解：378∘化成弧度为378×π180=21π10．
故选A．
2.
【答案】
A
【考点】
三角函数
【解析】
无
【解答】
解：由三角函数的定义得，sinα=yr=27=277，
csα=xr=−37=−217，
tanα=yx=−23=−233．
故选A．
3.
【答案】
D
【考点】
相等向量与相反向量
平行向量（共线向量）
空间向量的加减法
【解析】
此题暂无解析
【解答】
解：若|a→|=|b→|，只能表示a→和b→的长度相等，不能说明是相等向量，A错误；
相反向量是方向相反，模相等的两个向量，B错误；
若AB→=DC→，则A，B，C，D四点可能共线，不能构成平行四边形，C错误；
单位向量是模长等于1的向量．两个单位向量之和的模长可能仍然为1，D正确．
故选D .
4.
【答案】
B
【考点】
同角三角函数间的基本关系
运用诱导公式化简求值
【解析】
此题暂无解析
【解答】
解：因为sinα=45且π2<α<π，
所以csα=−1−sin2α=−35，
故csπ−α+2sinπ2+α
=−csα+2csα=csα=−35 .
故选B.
5.
【答案】
D
【考点】
频率分布折线图、密度曲线
【解析】
无
【解答】
解：由所给折线图可知，6岁到7岁，身高增长了2cm；7岁到8岁，身高增长了3cm；8岁到9岁，身高增长了5cm；9岁到10岁，身高增长了6cm；10岁到11岁，身高增长了9cm；11岁到12岁，身高增长了3cm．身高增长速度最快的是10岁到11岁，A错误；
从6岁到12岁，每年身高平均增长286=143cm，B错误；
随着年龄的增长，身高逐年增长，身高和年龄呈正相关，C错误；
6岁到9岁，身高增长了10cm，9岁到12岁，身高增长了18cm，D正确．
故选D．
6.
【答案】
B
【考点】
向量的共线定理
【解析】
此题暂无解析
【解答】
解：AB→=OB→−OA→=ne2→−e1→，AC→=OC→−OA→=14e2→−34e1→，
因为A，B，C三点共线，所以AB→=λAC→，
即ne2→−e1→=λ(14e2→−34e1→)，
所以ne2→−e1→=λ4e2→−3λ4e1→，
则n=λ4，−1=−3λ4，
解得n=13.
故选B.
7.
【答案】
D
【考点】
几何概型计算（与长度、角度、面积、体积有关的几何概型）
【解析】
无
【解答】
解：大正方形的边长是5，故大正方形的面积为25，
小正方形的边长为1，故小正方形的面积为1，
若在大正方形内随机取点，则这一点落在小正方形内的概率为125．
故选D．
8.
【答案】
C
【考点】
正弦函数的对称性
正弦函数的奇偶性
正弦函数的周期性
【解析】
无
【解答】
解：fx不是奇函数，A错误；
fx的最小正周期为π，B错误；
直线x=−π12是fx图象的对称轴，C正确；
fπ12=2sin2×π12−π3=2sin−π6=−1，
∴(π12,0)不是fx图象的对称中心，D错误．
故选C．
9.
【答案】
B
【考点】
程序框图
【解析】
无
【解答】
解：按照程序运行，S=2，i=1，判断条件不成立；
S=2+2×5，i=2，判断条件不成立；
S=2+2×5+2×52，i=3，判断条件不成立；
S=2+2×5+2×52+2×53，i=4，判断条件不成立；
S=2+2×5+2×52+2×53×2×54，i=5，判断条件不成立；
S=2+2×5+2×52+2×53+2×54+2×55，i=6，判断条件成立，跳出循环体输出结果．
因此，判断框内的条件应为“i>5？”．
故选B．
10.
【答案】
A
【考点】
向量的线性运算性质及几何意义
【解析】
无
【解答】
解：∵AD→=AB→+13BC→，BE→=BA→+13AC→，
∴AD→−BE→=AB→+13BC→−BA→−13AC→
=2AB→+13(BC→+CA→)
=2AB→+13BA→
=53AB→，
则AB→=35AD→−35BE→，
故λ+μ=0．
故选A．
11.
【答案】
B
【考点】
正切函数的周期性
正切函数的值域
正切函数的奇偶性与对称性
正切函数的图象
【解析】
无
【解答】
解：f(x)=tanx+|tanx|=2tanx，x∈[kπ,π2+kπ)，k∈Z，0，x∈(−π2+kπ,kπ)，k∈Z，
作出f(x)的图象，如图，
可得fx的最小正周期为π，①错误；
fx的图象没有对称中心，②错误；
fx的值域为[0,+∞)，③正确；
不等式fx>2的解集为π4+kπ,π2+kπk∈Z，④正确．
故选B．
12.
【答案】
B
【考点】
函数y=Asin（ωx+φ）的图象变换
余弦函数的图象
函数的零点
【解析】
无
【解答】
解：fx=3cs[πx+16−π3]−1=3csπx−π6−1，
令fx=0，
有csπx−π6=13，
在同一直角坐标系中作出函数y=csπx−π6与y=13的图象，
∴x1+x2+x3+x4+x5+x6
=2×−116+2×16+2×136=1.
故选B．
二、填空题
【答案】
7.2
【考点】
极差、方差与标准差
【解析】
无
【解答】
解：将该组数据中的每一个数据都加上1，新的数据的标准差保持不变，仍然是7.2．
故答案为：7.2．
【答案】
2
【考点】
平面向量数量积的运算
向量的模
【解析】
无
【解答】
解：∵b→⋅a→+b→
=a→⋅b→+b→2
=|a→|⋅|b→|csπ3+|b→|2
=|a→|+4
=6，
∴|a→|=2．
故答案为：2．
【答案】
34
【考点】
向量的三角形法则
平面向量数量积
【解析】
无
【解答】
解：AC→⋅DE→=AC→⋅DC→+CE→
=AC→⋅DC→+AC→⋅CE→
=AC→⋅AB→−12AC→⋅AD→
=|AC→|×|AB→|×cs30∘−12|AC→|×|AD→|×cs30∘
=3×1×32−12×3×1×32
=34.
故答案为：34．
【答案】
[32−1,+∞)
【考点】
函数恒成立问题
正弦函数的定义域和值域
【解析】
无
【解答】
解：当x∈[0,π12]时，2x+π6∈[π6,π3]，12≤sin2x+π6≤32，
此时fx的最大值为32+a，最小值为12+a，
对任意的x1，x2∈[0,π12]，fx1+fx2≥fx2恒成立，
则212+a≥32+a，
∴a≥32−1．
故答案为：[32−1,+∞)．
三、解答题
【答案】
解：(1)由a→⊥b→可得x−2=0，
解得x=2 ，
∴a→+b→=3,1 ，
故|a→+b→|=32+12=10．
(2)由a→//b→可得2x+1=0，
解得x=−12，
则b→=−12,−1，a→−b→=32,3 ，
∴a→−b→⋅a→=32×1+3×2=152．
【考点】
向量的数量积判断向量的共线与垂直
向量的模
平面向量数量积的运算
平行向量（共线向量）
【解析】
无
无
【解答】
解：(1)由a→⊥b→可得x−2=0，
解得x=2 ，
∴a→+b→=3,1 ，
故|a→+b→|=32+12=10．
(2)由a→//b→可得2x+1=0，
解得x=−12，
则b→=−12,−1，a→−b→=32,3 ，
∴a→−b→⋅a→=32×1+3×2=152．
【答案】
解：(1)∵sinα+4sinα2sinα−csα=2，
∴tanα+42tanα−1=2 ，
解得tanα=2 ，
故tanπ−α=−tanα=−2．
(2)2sin2α−cs2α
=2sin2α−cs2αsin2α+cs2
=2tan2α−1tan2α+1
=2×22−122+1
=75 ．
【考点】
同角三角函数间的基本关系
运用诱导公式化简求值
【解析】
无
无
【解答】
解：(1)∵sinα+4sinα2sinα−csα=2，
∴tanα+42tanα−1=2 ，
解得tanα=2 ，
故tanπ−α=−tanα=−2．
(2)2sin2α−cs2α
=2sin2α−cs2αsin2α+cs2
=2tan2α−1tan2α+1
=2×22−122+1
=75 ．
【答案】
解：(1)由图可得，平均数x¯=(100×0.0025+120×0.01+140×0.0225+160×0.015)×20=140台．
(2)销售量在(130,150]的销售人员有100×0.0225×20=45人，
销售量在(150, 170]的销售人员有100×0.015×20=30人，
分层抽样的比例为545+30=115，
所以从(130,150]组应抽取45×115=3人，
从(150.170]组应抽取30×115=2人．
记从(130,150]组抽取的3人为A1，A2，A3，从(150.170]组抽取的2人为B1，B2，
则从中任选2人基本事件共有10个，分别为：
(A1,A2)，(A1,A3)，(A1,B1)，(A1,B2)，(A2,A3)，
(A2,B1)，(A2,B2)，(A3,B1)，(A3,B2)，(B1,B2)，
其中不是来自同一组的情况共有6个，分别为：
(A1,B1)，(A1,B2)，(A2,B1)，(A2,B2)，(A3,B1)，(A3,B2)，
则这2人不是来自同一组的概率为610=35 ．
【考点】
加权平均数
列举法计算基本事件数及事件发生的概率
分层抽样方法
【解析】
无
无
【解答】
解：(1)由图可得，平均数x¯=(100×0.0025+120×0.01+140×0.0225+160×0.015)×20=140台．
(2)销售量在(130,150]的销售人员有100×0.0225×20=45人，
销售量在(150, 170]的销售人员有100×0.015×20=30人，
分层抽样的比例为545+30=115，
所以从(130,150]组应抽取45×115=3人，
从(150.170]组应抽取30×115=2人．
记从(130,150]组抽取的3人为A1，A2，A3，从(150.170]组抽取的2人为B1，B2，
则从中任选2人基本事件共有10个，分别为：
(A1,A2)，(A1,A3)，(A1,B1)，(A1,B2)，(A2,A3)，
(A2,B1)，(A2,B2)，(A3,B1)，(A3,B2)，(B1,B2)，
其中不是来自同一组的情况共有6个，分别为：
(A1,B1)，(A1,B2)，(A2,B1)，(A2,B2)，(A3,B1)，(A3,B2)，
则这2人不是来自同一组的概率为610=35 ．
【答案】
解：以A为坐标原点，分别以AB→，AC→的方向为x轴，y轴的正方向，建立平面直角坐标系xAy，
则A0,0，B1,0，C0,2，
设D(0,y)，则BD→=−1,y .
(1)∵BC→=−1,2，
∴cs⟨BD→，BC→⟩=|BD→⋅BC→||BD→||BC→|
=1+2y1+y2⋅12+22=22，
解得y=13，
即AD=13，
故λ=2−132=56．
(2)∵CD→=0,y−2，
∴BD→⋅CD→=y(y−2)=(y−1)2−1≥−1 ，
当y=1时取得最小值．
故BD→⋅CD→的最小值为−1．
【考点】
数量积表示两个向量的夹角
平面向量数量积的运算
二次函数在闭区间上的最值
【解析】
无
无
【解答】
解：以A为坐标原点，分别以AB→，AC→的方向为x轴，y轴的正方向，建立平面直角坐标系xAy，
则A0,0，B1,0，C0,2，
设D(0,y)，则BD→=−1,y .
(1)∵BC→=−1,2，
∴cs⟨BD→，BC→⟩=|BD→⋅BC→||BD→||BC→|
=1+2y1+y2⋅12+22=22，
解得y=13，
即AD=13，
故λ=2−132=56．
(2)∵CD→=0,y−2，
∴BD→⋅CD→=y(y−2)=(y−1)2−1≥−1 ，
当y=1时取得最小值．
故BD→⋅CD→的最小值为−1．
【答案】
解：(1)根据表中数据易得x¯=5，y¯=75，
i=15xiyi=2015，i=15xi2=135，
所以
b=i=15xiyi−5x¯⋅y¯i=15xi2−5x¯2=2015−5×5×75135−5×52=14，
a=y¯−bx¯=75−14×5=5.
故回归方程为y=14x+5.
(2)当0≤x≤10时，利润z=y−x−60%y=4.6x+2，
函数z=4.6x+2在[0, 10]上单调递增,
所以当x=10时，zmax=48；
当x>10时，利润z=y−x−60%y=−400x−x+98，
由函数的性质可得函数z=−400x−x+98在(10, 20)上单调递增，在(20, +∞)上单调递减，
所以zmax=−40020−20+98=58>48，此时x=20，
综上，为使企业获得最大利润，应投入20千万元广告费.
【考点】
求解线性回归方程
分段函数的应用
函数最值的应用
【解析】
此题暂无解析
【解答】
解：(1)根据表中数据易得x¯=5，y¯=75，
i=15xiyi=2015，i=15xi2=135，
所以
b=i=15xiyi−5x¯⋅y¯i=15xi2−5x¯2=2015−5×5×75135−5×52=14，
a=y¯−bx¯=75−14×5=5.
故回归方程为y=14x+5.
(2)当0≤x≤10时，利润z=y−x−60%y=4.6x+2，
函数z=4.6x+2在[0, 10]上单调递增,
所以当x=10时，zmax=48；
当x>10时，利润z=y−x−60%y=−400x−x+98，
由函数的性质可得函数z=−400x−x+98在(10, 20)上单调递增，在(20, +∞)上单调递减，
所以zmax=−40020−20+98=58>48，此时x=20，
综上，为使企业获得最大利润，应投入20千万元广告费.
【答案】
解：(1)由图可知A=2，T4=5π12−π6=π4，
则T=2πω=π，解得ω=2，
由f−5π12=−2知，2×−5π12+φ=−π2+2kπ，k∈Z，
解得φ=π3+2kπ，k∈Z.
又因为|φ|<π2，所以φ=π3，
所以fx=2sin2x+π3 .
令π2+2kπ≤2x+π3≤3π2+2kπ，k∈Z，
解得π12+kπ≤x≤7π12+kπ，k∈Z，
所以fx的单调递减区间为π12+kπ,7π12+kπ(k∈Z) .
(2)因为π6−α所以2π3−2α<2x+π3<2π3+2α，
因为在π6−α,π6+α上存在唯一的x0，使得fx0≥fx恒成立，
所以2α>2π3−π2，2α≤5π2−2π3，
解得π12<α≤11π12，
所以α的取值范围为π12,11π12 .
【考点】
由y=Asin（ωx+φ）的部分图象确定其解析式
正弦函数的单调性
函数的最值及其几何意义
函数最值的应用
【解析】
此题暂无解析
【解答】
解：(1)由图可知A=2，T4=5π12−π6=π4，
则T=2πω=π，解得ω=2，
由f−5π12=−2知，2×−5π12+φ=−π2+2kπ，k∈Z，
解得φ=π3+2kπ，k∈Z.
又因为|φ|<π2，所以φ=π3，
所以fx=2sin2x+π3 .
令π2+2kπ≤2x+π3≤3π2+2kπ，k∈Z，
解得π12+kπ≤x≤7π12+kπ，k∈Z，
所以fx的单调递减区间为π12+kπ,7π12+kπ(k∈Z) .
(2)因为π6−α所以2π3−2α<2x+π3<2π3+2α，
因为在π6−α,π6+α上存在唯一的x0，使得fx0≥fx恒成立，
所以2α>2π3−π2，2α≤5π2−2π3，
解得π12<α≤11π12，
所以α的取值范围为π12,11π12 . x（单位：千万元）
3
4
5
6
7
y（单位：千万元）
45
65
75
85
105