初中数学北师大版九年级上册第四章 图形的相似2 平行线分线段成比例当堂达标检测题

这是一份初中数学北师大版九年级上册第四章 图形的相似2 平行线分线段成比例当堂达标检测题，共11页。试卷主要包含了如图，BD＝CD，AE，如图，DF∥AC，DE∥BC等内容，欢迎下载使用。
1．如图，已知AB∥CD∥EF，若AC＝6，BD＝3，则BF的长为（ ）
A．6B．5.5C．4D．4.5
2．如图，已知D、E分别为AB、AC上的两点，且DE∥BC，AB＝8，则AD的长为（ ）
A．3B．4C．5D．6
3．如图，AB∥CD∥EF，AD＝4，则BE的长为（ ）
A．B．C．4D．6
4．如图，l1∥l2∥l3，两条直线与这三条平行线分别交于点A、B、C和D、E、F，若，则的值为（ ）
A．B．C．D．
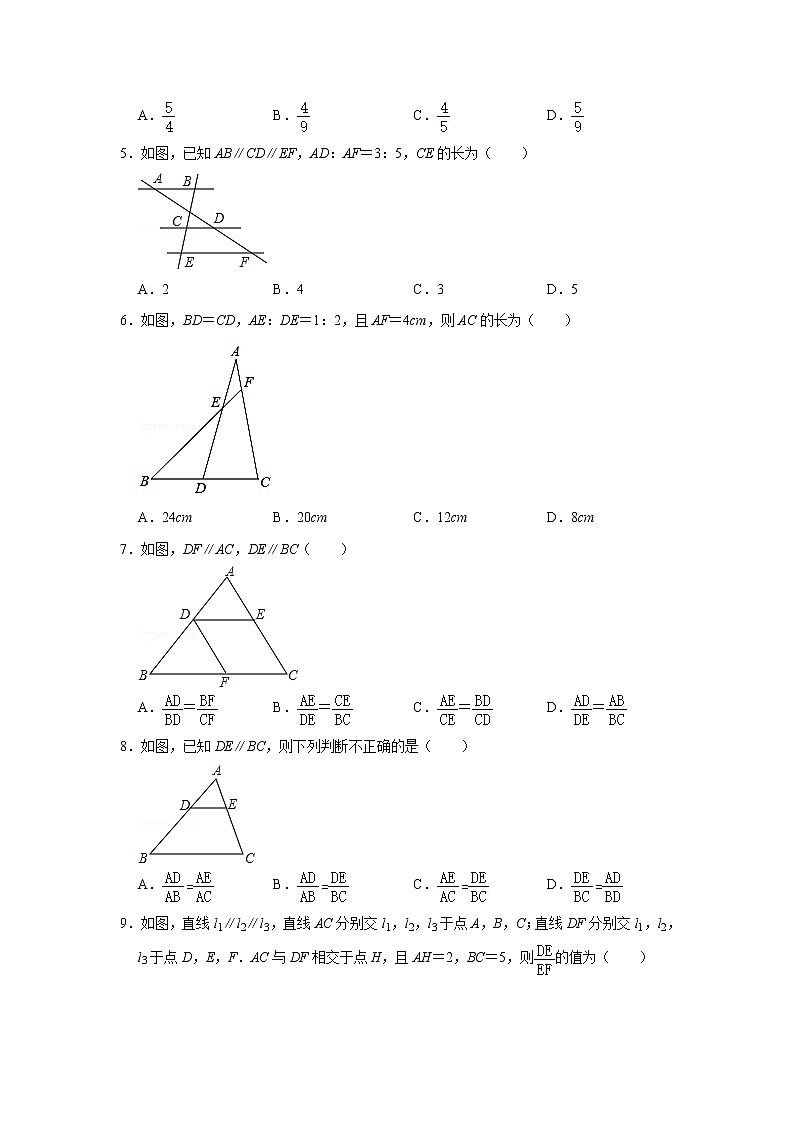
5．如图，已知AB∥CD∥EF，AD：AF＝3：5，CE的长为（ ）
A．2B．4C．3D．5
6．如图，BD＝CD，AE：DE＝1：2，且AF＝4cm，则AC的长为（ ）
A．24cmB．20cmC．12cmD．8cm
7．如图，DF∥AC，DE∥BC（ ）
A．＝B．＝C．＝D．＝
8．如图，已知DE∥BC，则下列判断不正确的是（ ）
A．B．C．D．
9．如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C；直线DF分别交l1，l2，l3于点D，E，F．AC与DF相交于点H，且AH＝2，BC＝5，则的值为（ ）
A．B．2C．D．
10．如图，已知AB∥CD，AD与BC相交于点O，那么下列式子正确的是（ ）
A．BO：BC＝1：2B．CD：AB＝2：1C．CO：BC＝1：2D．AD：DO＝3：1
11．如图，点F是▱ABCD的边CD上一点，直线BF交AD的延长线与点E（ ）
A．B．C．D．
12．在平行四边形ABCD中，E是AD上一点，连接CE并延长交BA的延长线于点F（ ）
A．∠AEF＝∠DECB．FA：CD＝AE：EC
C．FA：AB＝EF：ECD．AB＝DC
二．填空题（共4小题）
13．如图，在△ABC中，AD：DB＝2：3，AE的延长线交BC于点F，则BF：FC＝ ．
14．如图，已知在△ABC中，点D、E、F分别是边AB、AC、BC上的点，EF∥AB，且AD：DB＝3：5 ．
15．如图，AB∥GH∥CD，点H在BC上，AB＝2，CD＝4 ．
16．如图，体育兴趣小组选一名身高1.6m的同学直立于旗杆影子的顶端处，其他人分为两部分，另一部分同学测得同一时刻旗杆影长为9m，那么旗杆的高度是 m．
三．解答题（共4小题）
17．如图，已知AD∥BE∥CF，它们依次交直线l1、l2于点A、B、C和点D、E、F．
（1）如果AB＝6，BC＝8，DF＝7；
（2）如果AB：AC＝2：5，EF＝9，求DF的长．
18．如图，已知梯形ABCD中，AD∥BC，BD交于O，过O作AD的平行线交AB于M，BC＝5cm，求ON．
19．如图所示，已知AB∥EF∥CD，AC、BD相交于点E，CD＝12cm，求EF．
20．△ABC中，AB＝1，AC＝2，AE平分∠BAC交BC于E，且DF∥AE．求CF的长．
参考答案
一．选择题（共12小题）
1．解：∵AB∥CD∥EF，
∴＝，即＝，
∴BF＝4．
故选：C．
2．解：∵DE∥BC，
∴＝＝＝，
∴AD＝×8＝6．
故选：D．
3．解：∵AB∥CD∥EF，
∴＝，
∴＝，
∴EC＝，
∴BE＝BC+EC＝6+＝，
故选：A．
4．解：∵l1∥l2∥l6，
∴＝＝．
故选：C．
5．解：∵AB∥CD∥EF，
∴，
∴BE＝＝＝10，
∴CE＝BE﹣BC＝10﹣6＝6，
故选：B．
6．解：过D作DG∥BF交AC于G，则△AEF∽△ADG，
∵BD＝CD，
∴CG＝GF，AF：FG＝AE：ED＝1：2，
∵AF＝8cm，
∴FG＝2AF＝8cm＝CG，
∴AC＝AF+FG+CG＝20cm．
故选：B．
7．解：∵DF∥AC，
∴＝，所以A选项错误；
∵DE∥BC，
∴＝，所以C选项错误；
而＝，
∴＝，
∵DE∥CF，DF∥CE，
∴四边形DECF为平行四边形，
∴CF＝DE，
∴＝，即＝，所以B选项错误；
∵DE∥BC，
∴＝，即＝，所以D选项正确．
故选：D．
8．解：∵DE∥BC，
∴＝＝，
故A、B、C选项正确；
故选：D．
9．解：∵AH＝2，HB＝1，
∴AB＝8，
∵l1∥l2∥l3，
∴＝＝，
故选：D．
10．解：∵AB∥CD，
∴△AOB∽△DOC，
∴AB：CD＝AO：DO＝1：2，
∴CD：AB＝5：1，
故选：B．
11．解：∵四边形ABCD是平行四边形，
∴CD∥AB，AD∥BC，AD＝BC，
∴，故A正确；
∴，
∴，故B正确；
∴，故C错误；
∴，
∴，故D正确．
故选：C．
12．解：∵四边形ABCD是平行四边形，
∴AD∥BC，AB∥CD，
∴FA：CD＝EF：EC，
即FA：AB＝EF：EC，
∴FA：CD＝AE：DE，并不等于AE：EC，
又∠AEF与∠DEC是对顶角，所以∠AEF＝∠DEC．
故选：B．
二．填空题（共4小题）
13．解：在AE上取点G，使EG＝EF，
∵E为CD的中点，
∴DE＝CE，
又∵EG＝EF，∠DEG＝∠CEF，
∴△DGE≌△CFE，
∴DG＝FC，
根据比例关系可知：DG∥FC，
∵AD：DB＝2：3，
∴＝＝＝．
故答案为．
14．解：∵DE∥BC，
∴AE：EC＝AD：DB＝3：5，
∴CE：CA＝5：8，
∵EF∥AB，
∴CF：CB＝CE：CA＝5：2．
故答案为5：8．
15．解：∵AB∥CH∥CD，
∴，，
∴+＝+＝1，
∵AB＝2，CD＝8，
∴+＝5，
解得：GH＝；
故答案为：．
16．解：由题意得
∴1.6：4.2＝旗杆的高度：9．
∴旗杆的高度为12m．
三．解答题（共4小题）
17．解：（1）∵AD∥BE∥CF，
∴，
即＝，
解得：EF＝4；
（2）∵AD∥BE∥CF，
∴＝，
即＝，
解得；DF＝15．
18．解：∵MN∥AD，AD∥BC，
∴MN∥AD∥BC，
∵ON∥AD，
∴＝①，
∵ON∥BC，
∴＝②，
①+②得+＝+＝1，
即+＝1，
∴ON＝．
19．解：∵AB∥CD，
∴＝＝＝2，
∴＝＝＝，
∵AB∥EF，
∴＝，
即＝，
解得EF＝4cm．
20．解：分别过E作EH⊥AB于H，EG⊥AC于G，所以有EH＝EG．
从而有．
又由DF∥AE，得
所以CF＝CA＝＝．