高中数学9.1.2 余弦定理教课内容课件ppt

这是一份高中数学9.1.2 余弦定理教课内容课件ppt，共28页。PPT课件主要包含了千岛湖，情景问题，试一试等内容，欢迎下载使用。

(3) 正弦定理的变形：
(2) 三角形面积公式：
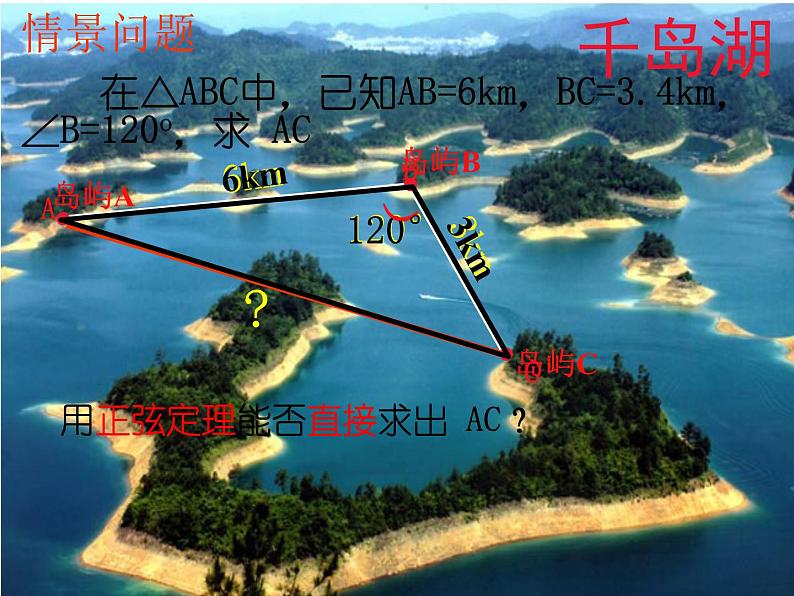
在△ABC中，已知AB=6km，BC=3.4km，∠B=120，求 AC
用正弦定理能否直接求出 AC？
如果已知一个三角形的两条边及其夹角，根据三角形全等的定理，该三角形大小形状完全确定，那么如何解出这个三角形呢？
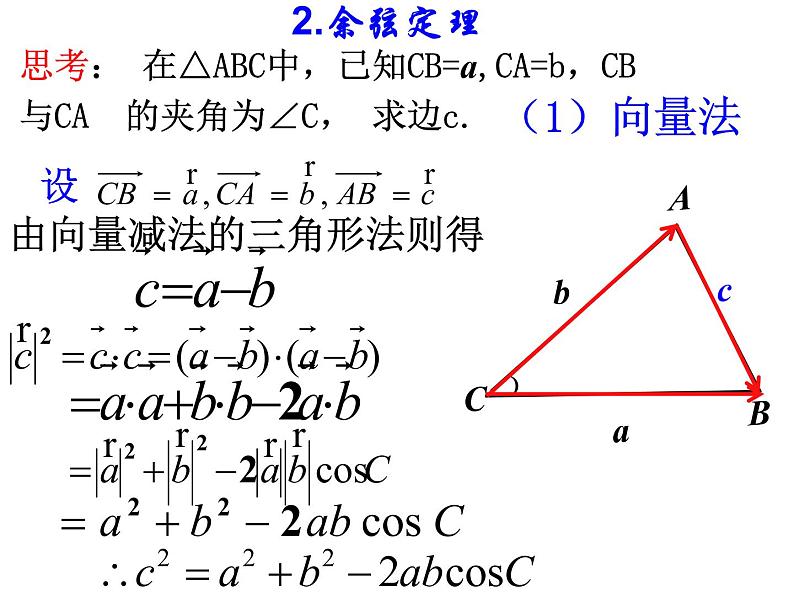
思考： 在△ABC中，已知CB=a,CA=b，CB与CA 的夹角为∠C， 求边c.
由向量减法的三角形法则得
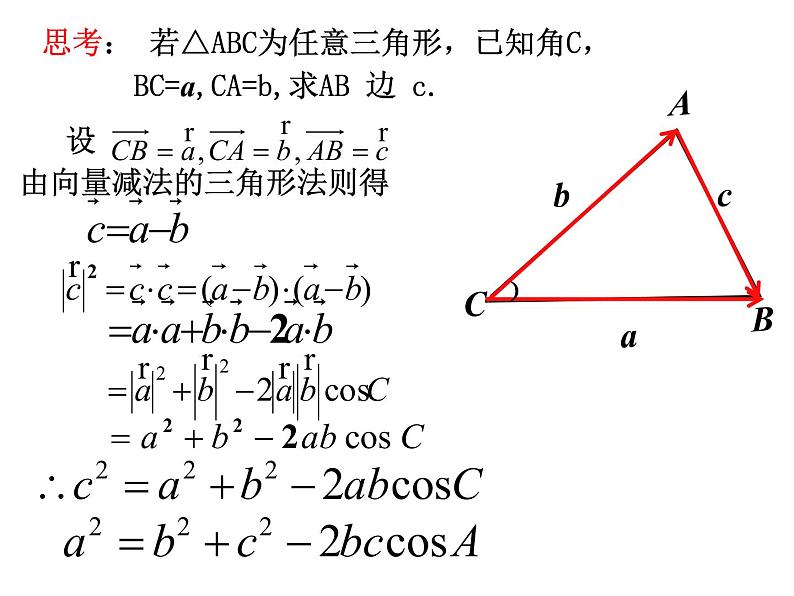
思考： 若△ABC为任意三角形，已知角C， BC=a,CA=b,求AB 边 c.
三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
证明：以CB所在的直线为x轴，过C点垂直于CB的直线为y轴，建立如图所示的坐标系，则A、B、C三点的坐标分别为：
例1，在△ABC中，已知AB=6km，BC=3km， ∠B=120，求 AC
答：岛屿A与岛屿C的距离为 km.
（1）已知两边和它们的夹角，求第三边和其他两个角；
2. 已知△ABC中，a=8,b=7,B＝600, 求c及S△ABC
整理得：c2-8c+15=0
解得：c1=3, c2=5
例 2.在△ABC中，已知a= ,b=2,c= ,解三角形
（2）已知三边，求三个角。
变式:在三角形ABC中，已知a=7,b=10,c=6 试判断△ABC的形状？
已知三角形的三边a,b,c且a>b,a>c判断三角形形状的步骤
1，根据大边对大角规则找到最大角A
2，看a2与b2+c2的大小关系
3，若a2>b2+c2则三角形是钝角三角形 若a2=b2+c2则三角形是直角三角形 若a2(A)300 (B)600 ©1200 (D)1500
3.三角形三边之比是3：5：7那么这个三角形一 定是（ ）(A)锐角三角形 (B)直角三角形©钝角三角形 (D)非锐角三角形
练.在△ABC中，已知a=7,b=8,csC= , 求最大角的余弦值
分析：求最大角的余弦值，最主要的是判断哪个角是最大角。由大边对大角，已知两边可求出第三边,找到最大角。
则有：b是最大边，那么B 是最大角
【反思·感悟】三角形中判断边、角关系的具体方法：(1)通过正弦定理实施边角转换；(2)通过余弦定理实施边角转换；(3)通过三角变换找出角之间的关系；(4)通过三角函数值符号的判断以及正、余弦函数有界性的讨论.
答案：三角形ABC为直角三角形
（3）余弦定理可以解决的有关三角形的问题： 已知两边及其夹角，求第三边和其他 两个角。2) 已知三边求三个角。3) 判断三角形的形状。