- 5.3.5 随机事件的独立性 学案 学案 1 次下载
- 5.4 统计与概率的应用 学案 学案 2 次下载
- 6.1.2 向量的加法 学案 学案 1 次下载
- 6.1.3 向量的减法 学案 学案 1 次下载
- 6.1.5 向量的线性运算 学案 学案 1 次下载
高中数学人教B版 (2019)必修 第二册第六章 平面向量初步6.1 平面向量及其线性运算6.1.1 向量的概念导学案及答案
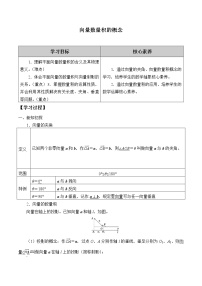
展开【学习目标】
1.理解向量的有关概念及向量的几何表示
2.理解共线向量、相等向量的概念
3.正确区分向量平行与直线平行
【学习重难点】
1.向量的概念
2.共线向量、相等向量
3.向量与几何的关系
【学习过程】
问题导学
预习教材P133-P136的内容,思考以下问题:
1.向量是如何定义的?怎样表示向量?
2.向量的相关概念有哪些?
3.两个向量能比较大小吗?
【新知初探】
1.位移与向量
(1)向量的概念
一般地,像位移这样既有大小又有方向的量称为向量(也称为矢量)。
向量的大小也称为向量的模(或长度);只有大小的量称为标量,长度、面积等都是标量。
(2)向量的表示方法
①始点为A终点为B的有向线段表示的向量,可以用符号简记为eq \(AB,\s\up6(→)),此时向量eq \(AB,\s\up6(→))的模用|eq \(AB,\s\up6(→))|表示。除了用始点和终点的两个大写字母来表示向量外,还可用一个小写字母来表示向量:在印刷时,通常用加粗的斜体小写字母如a,b,c等来表示向量;在书写时,用带箭头的小写字母如eq \(a,\s\up6(→)),eq \(b,\s\up6(→)),eq \(c,\s\up6(→))等来表示向量。
②始点和终点相同的向量称为零向量。零向量的模为0.零向量的方向是不确定。模不为0的向量通常称为非零向量。模等于1的向量称为单位向量。e是单位向量的充要条件是|e|=1.
■名师点拨
向量可以用有向线段表示,但向量不是有向线段。向量是规定了大小和方向的量,有向线段是规定了起点和终点的线段。
2.向量的相等与平行
一般地,把大小相等、方向相同的向量称为相等的向量。
如果两个非零向量的方向相同或相反,则称这两个向量平行。因为零向量的方向不确定,因此通常规定零向量与任意向量平行。两个向量a和b平行,记作a∥B.两个向量平行也称为两个向量共线。
■名师点拨
共线向量仅仅指向量的方向相同或相反;相等向量指大小和方向均相同。
【自我检测】
1.判断正误(正确的打“√”,错误的打“×”)
(1)零向量没有方向。( )
(2)向量eq \(AB,\s\up6(→))的长度和向量eq \(BA,\s\up6(→))的模相等。( )
(3)单位向量都平行。( )
(4)零向量与任意向量都平行。( )
2.在下列物理量:①质量;②温度;③角度;④弹力;⑤风速。其中可以看成是向量的有( )
A.1个
B.2个
C.3个
D.4个
3.关于零向量,下列说法中错误的是( )
A.零向量是没有方向的
B.零向量的长度为0
C.零向量只与零向量相等
D.零向量的方向是任意的
4.如图,四边形ABCD是平行四边形,则图中相等的向量是________(填序号)。
①eq \(AD,\s\up6(→))与eq \(BC,\s\up6(→));②eq \(OB,\s\up6(→))与eq \(OD,\s\up6(→));
③eq \(AC,\s\up6(→))与eq \(BD,\s\up6(→));④eq \(AO,\s\up6(→))与eq \(OC,\s\up6(→))。
探究一:向量的有关概念
1.判断下列命题是否正确,请说明理由:
(1)若向量a与b同向,且|a|>|b|,则a>b;
(2)若向量|a|=|b|,则a与b的长度相等且方向相同或相反;
(3)对于任意向量|a|=|b|,若a与b的方向相同,则a=b;
(4)向量a与向量b平行,则向量a与b方向相同或相反。
[规律方法]eq \a\vs4\al()
(1)理解零向量和单位向量应注意的问题
①零向量的方向是任意的,所有的零向量都相等。
②单位向量不一定相等,易忽略向量的方向。
(2)共线向量与平行向量
①平行向量也称为共线向量,两个概念没有区别。
②共线向量所在直线可以平行,与平面几何中的共线不同。
③平行向量可以共线,与平面几何中的直线平行不同。
2.给出下列命题:
①若a∥b,b∥c,则a∥c;
②若单位向量的起点相同,则终点相同;
③起点不同,但方向相同且模相等的几个向量是相等向量;
④向量eq \(AB,\s\up6(→))与eq \(CD,\s\up6(→))是共线向量,则A,B,C,D四点必在同一直线上。
其中正确命题的序号是________。
探究二、向量的表示及应用
1.(1)如图,B,C是线段AD的三等分点,分别以图中各点为起点和终点,可以写出________个向量。
(2)在如图所示的坐标纸上(每个小方格边长为1),用直尺和圆规画出下列向量:
①eq \(OA,\s\up6(→)),使|eq \(OA,\s\up6(→))|=4eq \r(2),点A在点O北偏东45°处;
②eq \(AB,\s\up6(→)),使|eq \(AB,\s\up6(→))|=4,点B在点A正东处;
③eq \(BC,\s\up6(→)),使|eq \(BC,\s\up6(→))|=6,点C在点B北偏东30°处。
[规律方法]
eq \a\vs4\al()(1)向量的两种表示方法
①几何表示法:先确定向量的起点,再确定向量的方向,最后根据向量的长度确定向量的终点。
②字母表示法:为了便于运算可用字母a,b,c表示,为了联系平面几何中的图形性质,可用表示向量的有向线段的起点与终点表示向量,如eq \(AB,\s\up6(→)),eq \(CD,\s\up6(→)),eq \(EF,\s\up6(→))等。
(2)两种向量表示方法的作用
①用几何表示法表示向量,便于用几何方法研究向量运算,为用向量处理几何问题打下了基础。
②用字母表示法表示向量,便于向量的运算。
2.某人从A点出发向东走了5米到达B点,然后改变方向按东北方向走了10eq \r(2)米到达C点,到达C点后又改变方向向西走了10米到达D点。
(1)作出向量eq \(AB,\s\up6(→)),eq \(BC,\s\up6(→)),eq \(CD,\s\up6(→));
(2)求eq \(AD,\s\up6(→))的模。
探究三、相等向量和共线向量
3.如图所示,O是正六边形ABCDEF的中心,且eq \(OA,\s\up6(→))=a,eq \(OB,\s\up6(→))=b,eq \(OC,\s\up6(→))=C.
(1)与a的长度相等、方向相反的向量有哪些?
(2)与a共线的向量有哪些?
(3)请一一列出与a,b,c相等的向量。
[互动探究]
1.[变问法]本例条件不变,试写出与向量eq \(BC,\s\up6(→))相等的向量。
2.[变条件,变问法]在本例中,若|a|=1,求正六边形的边长。
[规律方法]
eq \a\vs4\al()相等向量与共线向量的探求方法
(1)寻找相等向量:先找与表示已知向量的有向线段长度相等的向量,再确定哪些是同向共线。
(2)寻找共线向量:先找与表示已知向量的有向线段平行或共线的线段,再构造同向与反向的向量,注意不要漏掉以表示已知向量的有向线段的终点为起点,起点为终点的向量。
3.如图所示,四边形ABCD与ABDE是平行四边形。
(1)找出与向量eq \(AB,\s\up6(→))共线的向量;
(2)找出与向量eq \(AB,\s\up6(→))相等的向量。
【达标测评】
1.下列结论正确的个数是( )
①温度含零上和零下温度,所以温度是向量;
②向量的模是一个正实数;
③向量a与b不共线,则a与b都是非零向量;
④若|a|>|b|,则a>b.
A.0
B.1
C.2
D.3
2.设O是正方形ABCD的中心,则向量eq \(AO,\s\up6(→)),eq \(BO,\s\up6(→)),eq \(OC,\s\up6(→)),eq \(OD,\s\up6(→))是( )
A.相等的向量
B.平行的向量
C.有相同起点的向量
D.模相等的向量
3.在下列判断中,正确的是( )
①长度为0的向量都是零向量;
②零向量的方向都是相同的;
③单位向量的长度都相等;
④单位向量都是同方向向量;
⑤任意向量与零向量都共线。
A.①②③
B.②③④
C.①②⑤
D.①③⑤
4.在下列命题中:
①平行向量一定相等;②不相等的向量一定不平行;③共线向量一定相等;④相等向量一定共线;⑤长度相等的向量是相等向量;⑥平行于同一个非零向量的两个向量是共线向量。
正确命题的序号是________。
【参考答案】
【自我检测】
1.答案:(1)×
(2)√
(3)×
(4)√
2.解析:选B.①②③不可以看成向量,④⑤可以看成向量。
3.答案:A
4.答案:①④
探究一:向量的有关概念
1.【解】(1)不正确。因为向量由两个因素来确定,即大小和方向,所以两个向量不能比较大小。
(2)不正确。由|a|=|b|只能判断两向量的长度相等,不能确定它们的方向关系。
(3)正确。因为|a|=|b|,且a与b同向,由两向量相等的条件,可得a=b.
(4)不正确。因为向量a与向量b若有一个是零向量,则其方向不定。
2.解析:①错误。若b=0,则①不成立。
②错误。起点相同的单位向量,终点未必相同。
③正确。对于一个向量只要不改变其大小和方向,是可以任意移动的。
④错误。共线向量即平行向量,只要求方向相同或相反即可。并不要求两个向量eq \(AB,\s\up6(→)),eq \(CD,\s\up6(→))必须在同一直线上。
答案:③
探究二、向量的表示及应用
1.【解】(1)可以写出12个向量,分别是:eq \(AB,\s\up6(→)),eq \(AC,\s\up6(→)),eq \(AD,\s\up6(→)),eq \(BC,\s\up6(→)),eq \(BD,\s\up6(→)),eq \(CD,\s\up6(→)),eq \(BA,\s\up6(→)),eq \(CA,\s\up6(→)),eq \(DA,\s\up6(→)),eq \(CB,\s\up6(→)),eq \(DB,\s\up6(→)),eq \(DC,\s\up6(→)),故填12.
(2)①由于点A在点O北偏东45°处,所以在坐标纸上点A距点O的横向小方格数与纵向小方格数相等。又|eq \(OA,\s\up6(→))|=4eq \r(2),小方格边长为1,所以点A距点O的横向小方格数与纵向小方格数都为4,于是点A位置可以确定,画出向量eq \(OA,\s\up6(→))如图所示。
②由于点B在点A正东处,且|eq \(AB,\s\up6(→))|=4,所以在坐标纸上点B距点A的横向小方格数为4,纵向小方格数为0,于是点B位置可以确定,画出向量eq \(AB,\s\up6(→))如图所示。
③由于点C在点B北偏东30°处,且|eq \(BC,\s\up6(→))|=6,依据勾股定理可得,在坐标纸上点C距点B的横向小方格数为3,纵向小方格数为3eq \r(3)≈5.2,于是点C位置可以确定,画出向量eq \(BC,\s\up6(→))如图所示。
2.解:(1)作出向量eq \(AB,\s\up6(→)),eq \(BC,\s\up6(→)),eq \(CD,\s\up6(→)),如图所示:
(2)由题意得,△BCD是直角三角形,其中∠BDC=90°,BC=10eq \r(2)米,CD=10米,所以BD=10米。△ABD是直角三角形,其中∠ABD=90°,AB=5米,BD=10米,所以AD=eq \r(52+(10)2)=5eq \r(5)(米),所以|eq \(AD,\s\up6(→))|=5eq \r(5)米。
3.【解】(1)与a的长度相等、方向相反的向量有eq \(OD,\s\up6(→)),eq \(BC,\s\up6(→)),eq \(AO,\s\up6(→)),eq \(FE,\s\up6(→))。
(2)与a共线的向量有eq \(EF,\s\up6(→)),eq \(BC,\s\up6(→)),eq \(OD,\s\up6(→)),eq \(FE,\s\up6(→)),eq \(CB,\s\up6(→)),eq \(DO,\s\up6(→)),eq \(AO,\s\up6(→)),eq \(DA,\s\up6(→)),eq \(AD,\s\up6(→))。
(3)与a相等的向量有eq \(EF,\s\up6(→)),eq \(DO,\s\up6(→)),eq \(CB,\s\up6(→));与b相等的向量有eq \(DC,\s\up6(→)),eq \(EO,\s\up6(→)),eq \(FA,\s\up6(→));与c相等的向量有eq \(FO,\s\up6(→)),eq \(ED,\s\up6(→)),eq \(AB,\s\up6(→))。
[互动探究]
1.解:与向量eq \(BC,\s\up6(→))相等的向量有eq \(OD,\s\up6(→)),eq \(AO,\s\up6(→)),eq \(FE,\s\up6(→))。
2.解:由正六边形性质知,△FOA为等边三角形,所以边长AF=|a|=1.
3.解:(1)依据图形可知eq \(DC,\s\up6(→)),eq \(ED,\s\up6(→)),eq \(EC,\s\up6(→))与eq \(AB,\s\up6(→))方向相同,eq \(BA,\s\up6(→)),eq \(CD,\s\up6(→)),eq \(DE,\s\up6(→)),eq \(CE,\s\up6(→))与eq \(AB,\s\up6(→))方向相反,所以与向量eq \(AB,\s\up6(→))共线的向量为eq \(BA,\s\up6(→)),eq \(CD,\s\up6(→)),eq \(DC,\s\up6(→)),eq \(ED,\s\up6(→)),eq \(DE,\s\up6(→)),eq \(EC,\s\up6(→)),eq \(CE,\s\up6(→))。
(2)由四边形ABCD与ABDE是平行四边形,知eq \(DC,\s\up6(→)),eq \(ED,\s\up6(→))与eq \(AB,\s\up6(→))长度相等且方向相同,所以与向量eq \(AB,\s\up6(→))相等的向量为eq \(DC,\s\up6(→))和eq \(ED,\s\up6(→))。
【达标测评】
1.解析:选B.①错误。温度是数量不是向量;②错误。零向量的模为0.③正确。因为零向量与任意向量共线;④错误。向量不能比较大小。
2.解析:选D.由正方形的性质知|eq \(AO,\s\up6(→))|=|eq \(BO,\s\up6(→))|=|eq \(OC,\s\up6(→))|=|eq \(OD,\s\up6(→))|。
3.解析:选D.由定义知①正确,②由于零向量的方向是任意的,故两个零向量的方向是否相同不确定,故不正确。显然③⑤正确,④不正确,故选D.
4.解析:由向量的相关概念可知④⑥正确。
答案:④⑥
高中数学人教B版 (2019)必修 第二册6.1.1 向量的概念导学案: 这是一份高中数学人教B版 (2019)必修 第二册6.1.1 向量的概念导学案,共15页。学案主要包含了位移与向量,向量的应用,向量的相等与平行等内容,欢迎下载使用。
2020-2021学年第六章 平面向量初步6.1 平面向量及其线性运算6.1.1 向量的概念学案: 这是一份2020-2021学年第六章 平面向量初步6.1 平面向量及其线性运算6.1.1 向量的概念学案,共3页。学案主要包含了学习目标,学习过程,作业布置等内容,欢迎下载使用。
2020-2021学年6.1.1 向量的概念导学案: 这是一份2020-2021学年6.1.1 向量的概念导学案,共3页。学案主要包含了学习目标,学习重难点,学习过程等内容,欢迎下载使用。