2019-2020学年天津市和平二十一中九上期末数学试卷

这是一份2019-2020学年天津市和平二十一中九上期末数学试卷，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共12小题；共60分）
1. 下列关于 x 的方程：① ax2+bx+c=0；② 3x−92−x+12=1；③ x+3=2x；④ a2+a+1x2−a=0；⑤ x+1=x−1，其中一元二次方程的个数是
A. 1B. 2C. 3D. 4

2. 从标号分别为 1，2，3，4，5 的 5 张卡片中，随机抽取 1 张．下列事件中，必然事件是
A. 标号小于 6B. 标号大于 6C. 标号是奇数D. 标号是 3

3. 如果关于 x 的方程 x2−4x+m=0 有两个不相等的实数根，那么在下列数值中，m 可以取的是
A. 3B. 5C. 6D. 8

4. 已知 ab=23，则代数式 a+bb 的值为
A. 52B. 53C. 23D. 32

5. 某型号的手机经过连续两次降价，每个售价由原来的 1185 元降到了 580 元，设平均每次降价的百分率为 x，列出方程正确的是
A. 5801+x2=1185B. 11851+x2=580
C. 5801−x2=1185D. 11851−x2=580

6. 如图，现分别旋转两个标准的转盘，两个转盘分别被分成两等份和三等份，则转盘所转到的两个数字之积为奇数的概率是
A. 35B. 13C. 12D. 16

7. 正三角形的高、外接圆半径、边心距之比为
A. 3:2:1B. 4:3:2C. 4:2:1D. 6:4:3

8. 下列说法正确的是
A. 三点确定一个圆
B. 一个三角形只有一个外接圆
C. 和半径垂直的直线是圆的切线
D. 三角形的内心到三角形三个顶点距离相等

9. 同一平面直角坐标系中，一次函数 y=ax+1 与二次函数 y=x2+a 的图象可能是
A. B.
C. D.

10. 如图是二次函数 y=ax2+bx+c 的部分图象，由图象可知不等式 ax2+bx+c<0 的解集是
A. −15
C. x<−1 且 x>5D. x<−1 或 x>5

11. 已知二次函数 y=kx2−7x−7 的图象与 x 轴没有交点，则 k 的取值范围为
A. k>−74B. k≥−74 且 k≠0
C. k<−74D. k>−74 且 k≠0

12. 二次函数 y=ax2+bx+c（a，b，c 为常数，且 a≠0）中的 x 与 y 的部分对应值如下表：
x−1013y−1353
下列结论：
（1）ac<0；
（2）当 x>1 时，y 的值随 x 值的增大而减小；
（3）x=3 是方程 ax2+b−1x+c=0 的一个根；
（4）当 −10．
其中正确的有
A. 4 个B. 3 个C. 2 个D. 1 个

二、填空题（共6小题；共30分）
13. 二次函数 y=−2x−12+3 的图象的顶点坐标是 ．

14. 中心角为 45∘ 的正多边形的边数是 ．

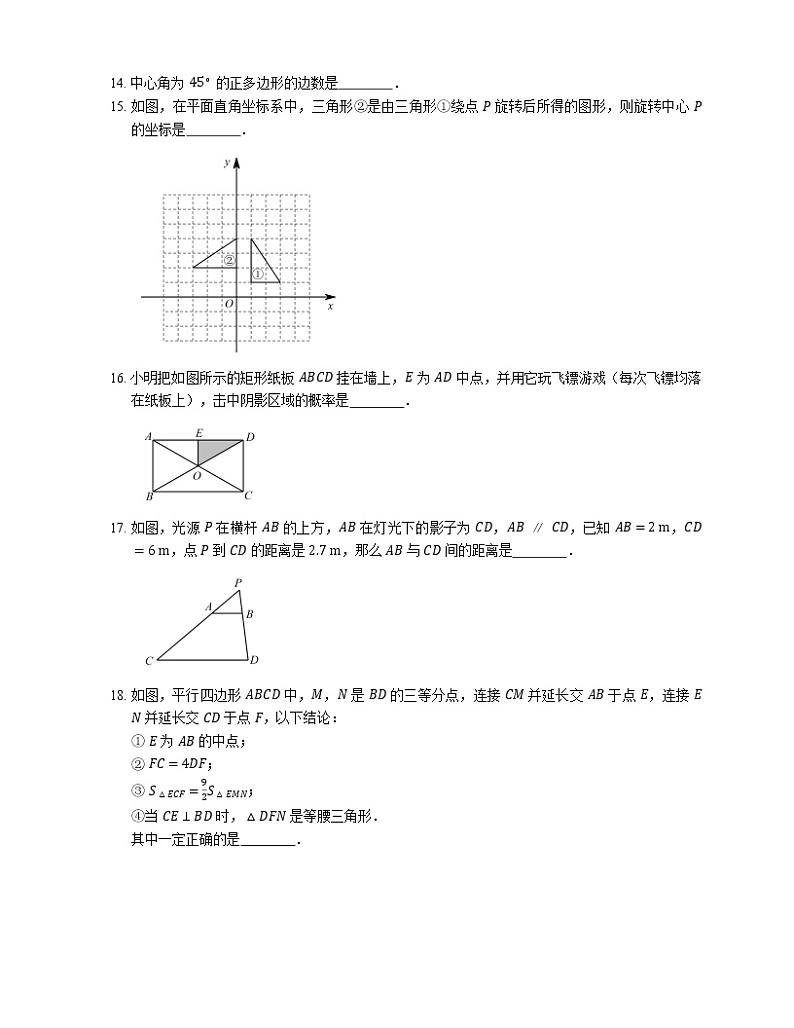
15. 如图，在平面直角坐标系中，三角形②是由三角形①绕点 P 旋转后所得的图形，则旋转中心 P 的坐标是 ．

16. 小明把如图所示的矩形纸板 ABCD 挂在墙上，E 为 AD 中点，并用它玩飞镖游戏（每次飞镖均落在纸板上），击中阴影区域的概率是 ．

17. 如图，光源 P 在横杆 AB 的上方，AB 在灯光下的影子为 CD，AB∥CD，已知 AB=2 m，CD=6 m，点 P 到 CD 的距离是 2.7 m，那么 AB 与 CD 间的距离是 ．

18. 如图，平行四边形 ABCD 中，M，N 是 BD 的三等分点，连接 CM 并延长交 AB 于点 E，连接 EN 并延长交 CD 于点 F，以下结论：
① E 为 AB 的中点；
② FC=4DF；
③ S△ECF=92S△EMN；
④当 CE⊥BD 时，△DFN 是等腰三角形．
其中一定正确的是 ．

三、解答题（共7小题；共91分）
19. 如图，一次函数 y1=−x+2 的图象与反比例函数 y2=mx 的图象交于点 A−1,3，Bn,−1．
（1）求反比例函数的解析式；
（2）当 y1>y2 时，直接写出 x 的取值范围．

20. （1）解方程：x2+4x−5=0（配方法）．
（2）已知：关于 x 的方程 2x2+kx−1=0．
① 求证：方程有两个不相等的实数根；② 若方程的一个根是 x=−1，求另一个根及 k 值．

21. 如图，Rt△ABC 内接于 ⊙O，点 D 是 Rt△ABC 斜边 AB 上的一点，过点 D 作 AB 的垂线交 AC 于 E，过点 C 作 ∠ECP=∠AED，CP 交 DE 的延长线于点 P，连接 PO 交 ⊙O 于点 F．
（1）求证：PC 是 ⊙O 的切线；
（2）若 PC=3，PF=1，求 AB 的长．

22. 如图，正方形 ABCD 中，M 为 BC 上一点，F 是 AM 的中点，EF⊥AM，垂足为 F，交 AD 的延长线于点 E，交 DC 于点 N．
（1）求证：△ABM∽△EFA．
（2）若 AB=12，BM=5，求 DE 的长．

23. 某校在基地参加社会实践活动中，带队老师问学生：基地计划新建一个矩形的生物园地，一边靠旧墙（墙足够长），另外三边用总长 69 米的不锈钢栅栏围成，与墙平行的一边留一个宽为 3 米的出入口，如图所示，如何设计才能使园地的面积最大?下面是两位学生争议的情境：
请根据上面的信息，解决问题：
（1）设 AB=x 米（x>0）， 试用含 x 的代数式表示 BC 的长；
（2）请你判断谁的说法正确，为什么?

24. 已知，等腰直角 △ABC 中，点 O 是斜边的中点，△MPN 是直角三角形，固定 △ABC，滑动 △MPN，在滑动过程中始终保持点 P 在直线 AC 上，且 PE⊥AB，PF⊥BC，垂足分别为 E，F．
（1）如图 1，当点 P 与点 O 重合时，OE，OF 的数量和位置关系分别是 ；
（2）当 △MPN 移动到图 2 的位置时，（1）中的结论还成立吗?请说明理由；
（3）如图 3，等腰直角 △ABC 的腰长为 6，点 P 在 AC 的延长线上时，Rt△MPN 的边 PM 与 AB 的延长线交于点 E，直线 BC 与直线 NP 交于点 F，OE 交 BC 于点 H，且 EH:HO=2:5，则 BE 的长是多少?

25. 如图，已知二次函数 y=−x2+bx+c（b，c 为常数）的图象经过点 A3,1，点 C0,4，顶点为 M，过点 A 作 AB∥x 轴，交 y 轴于点 D，交该二次函数图象于点 B，连接 BC．
（1）求该二次函数的解析式及点 M 的坐标；
（2）若将该二次函数图象向下平移 m（m>0）个单位，使平移后得到的二次函数图象的顶点落在 △ABC 的内部（不包括 △ABC 的边界），求 m 的取值范围；
（3）点 P 是直线 AC 上的动点，若以点 P，点 C，点 M 构成的三角形与 △BCD 相似，请直接写出所有点 P 的坐标（直接写出结果，不必写解答过程）．
答案
第一部分
1. B
2. A
3. A
4. B
5. D
6. B
7. A
8. B
9. C
10. D
【解析】由图象得：对称轴是 x=2，其中一个点的坐标为 5,0，
∴ 图象与 x 轴的另一个交点坐标为 −1,0．
利用图象可知：
ax2+bx+c<0 的解集即是 y<0 的解集，
∴ x<−1 或 x>5．
11. C
12. B
第二部分
13. 1,3
14. 八边形
15. 0,1
16. 18
17. 1.8 m
18. ①③④
第三部分
19. （1） 把 A−1,3 代入 y2=mx 可得 m=−1×3=−3，
所以反比例函数解析式为 y=−3x．
（2） 把 Bn,−1 代入 y=−3x 得 −n=−3，
解得 n=3，
则 B 的坐标为 3,−1，
所以当 x<−1 或 0y2．
20. （1） 移项，得
x2+4x=5.x2+4x+4=5+4.x+22=9.x+2=±3.
解得
x1=1,x2=−5.
（2） ①∵Δ=k2+8>0，
∴ 方程有两个不相等的实数根；
② 当 x=−1 时，2×−12−k−1=0，
解得：k=1，
则原方程为：2x2+x−1=0，
即 2x−1x+1=0，
解得：x1=0.5，x2=−1，
所以另一个根为 x=0.5，k 值为 1．
21. （1） 如图，连接 OC，
∵ PD⊥AB，
∴ ∠ADE=90∘，
∵ OA=OC，
∴ ∠EAD=∠ACO，
∵ ∠ECP=∠AED，
∴ ∠PCO=∠ECP+∠ACO=∠AED+∠EAD=90∘，
∴ PC⊥OC，
∴ PC 是 ⊙O 切线．
（2） 设 ⊙O 的半径为 x，则 OC=x，OP=1+x，
∵ PC=3，且 OC⊥PC，
∴ 在 Rt△POC 中由勾股定理得 32+x2=1+x2，
解得 x=4，
∴ AB=2x=8．
22. （1） 因为四边形 ABCD 是正方形，
所以 AB=AD，∠B=90∘，AD∥BC .
所以 ∠AMB=∠EAF .
又 EF⊥AM，
所以 ∠AFE=90∘ .
所以 ∠B=∠AFE .
所以 △ABM∽△EFA．
（2） 因为 ∠B=90∘，AB=12，BM=5，
所以 AM=122+52=13，AD=12 .
因为 F 是 AM 的中点，
所以 AF=12AM=6.5 .
因为 △ABM∽△EFA，
所以 BMAF=AMAE，
即 56.5=13AE .
所以 AE=16.9 .
所以 DE=AE−AD=4.9．
23. （1） 设 AB=x 米，可得 BC=69+3−2x=72−2x 米；
（2） 小英说法正确；理由如下：
矩形面积 S=x72−2x=−2x−182+648，
∵ 69−2x>0，
∴ x<34.5，
∴ 0∴当 x=18 时，S 取最大值，
此时 x≠72−2x，
∴面积最大的不是正方形．
24. （1） 相等且垂直
（2） 成立，理由如下：
∵△MPN 是直角三角形，
∴∠MPN=90∘．
如图，连接 OB，
∴∠OBE=∠C=45∘，
∵△ABC，△MPN 是直角三角形，PE⊥AB，PF⊥BC，
∴∠ABC=∠MPN=∠BEP=∠BFP=90∘，
∴ 四边形 EBFP 是矩形，
∴BE=PF，
∵PF=CF，
∴BE=CF，
∵ O 为 AC 中点，
∴ OB=OC=12AC，
在 △OEB 和 △OFC 中，
BE=CF,∠OBE=∠OCF,OB=OC,
∴△OEB≌△OFC，
∴ OE=OF，∠EOB=∠FOC，
∴ ∠EOB+∠BOF=∠FOC+∠BOF，即 ∠EOF=∠BOC=90∘，
∴ EO⊥FO．
（3） 如图，找 BC 的中点 G，连接 OG，
∵O 是 AC 中点，
∴OG∥AB，OG=12AB，
∵AB=6，
∴OG=3，
∵OG∥AB，
∴△BHE∽△GOH，
∵EH:HO=2:5，
∴BE:OG=2:5，
∴ BE=65．
25. （1） 把点 A3,1，点 C0,4 代入二次函数 y=−x2+bx+c 得，−32+3b+c=1,c=4 解得 b=2,c=4.
∴ 二次函数解析式为 y=−x2+2x+4，
配方得 y=−x−12+5，
∴ 点 M 的坐标为 1,5．
（2） 设直线 AC 解析式为 y=kx+n，把点 A3,1，C0,4 代入得，3k+n=1,n=4 解得 k=−1,n=4.
∴ 直线 AC 的解析式为 y=−x+4，如图所示，
对称轴直线 x=1 与 △ABC 两边 AC，AB 分别交于点 E，点 F．
把 x=1 代入直线 AC 解析式 y=−x+4 解得 y=3，则点 E 坐标为 1,3，点 F 坐标为 1,1．
∴ 1<5−m<3，解得 2 （3） P 点坐标有 4 个，分别为 P113,113，P2−13,133，P33,1，P4−3,7．