2019-2020学年天津市河北区双建中学九上期末数学试卷

这是一份2019-2020学年天津市河北区双建中学九上期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 用电器的输出功率 P 与通过的电流 I 、用电器的电阻 R 之间的关系是 P=I2R，下面说法正确的是
A. P 为定值时，I 与 R 成反比B. P 为定值时，I2 与 R 成反比
C. P 为定值时，I 与 R 成正比D. P 为定值时，I2 与 R 成正比

2. 下列说法正确的是
A. 分别在 △ABC 的边 AB，AC 的反向延长线上取点 D，E，使 DE∥BC，则 △ADE 是 △ABC 放大后的图形
B. 两个位似图形的面积之比等于位似比
C. 位似多边形中对应对角线之比等于位似比
D. 位似图形的周长之比等于位似比的平方

3. 下列命题中，正确的个数是
① 13 个人中至少有 2 人的生日是同一个月是必然事件；
②为了解我班学生的数学成绩，从中抽取 10 名学生的数学成绩是总体的一个样本；
③一名篮球运动员投篮命中概率为 0.7，他投篮 10 次，一定会命中 7 次；
④小颖在装有 10 个黑、白球的袋中，多次进行摸球试验，发现摸到黑球的频率在 0.6 附近波动，据此估计黑球约有 6 个．
A. 1B. 2C. 3D. 4

4. 如图，在 △ABC 中，点 D，E，F 分别在边 AB，AC，BC 上，且 DE∥BC，EF∥AB．若 AD=2BD，则 CFBF 的值为
A. 12B. 13C. 14D. 23

5. 若点 x1,y1 、 x2,y2 、 x3,y3 都是反比例函数 y=−a2−1x 的图象上的点，并且 x1<0A. y1
6. 在中华经典美文阅读中，小明同学发现自己的一本书的宽与长之比为黄金比．已知这本书的长为 20 cm，则它的宽约为
A. 12.36 cmB. 13.6 cmC. 32.36 cmD. 7.64 cm

7. 如图，一扇形纸扇完全打开后，外侧两竹条 AB 和 AC 的夹角为 120∘，AB 长为 25 cm，贴纸部分的宽 BD 为 15 cm，若纸扇两面贴纸，则贴纸的面积为
A. 175π cm2B. 350π cm2C. 8003π cm2D. 150π cm2

8. 一天晚上，小丽在清洗两只颜色分别为粉色和白色的有盖茶杯时，突然停电了，小丽只好把杯盖和茶杯随机搭配在一起，则其颜色搭配一致的概率是
A. 14B. 12C. 34D. 1

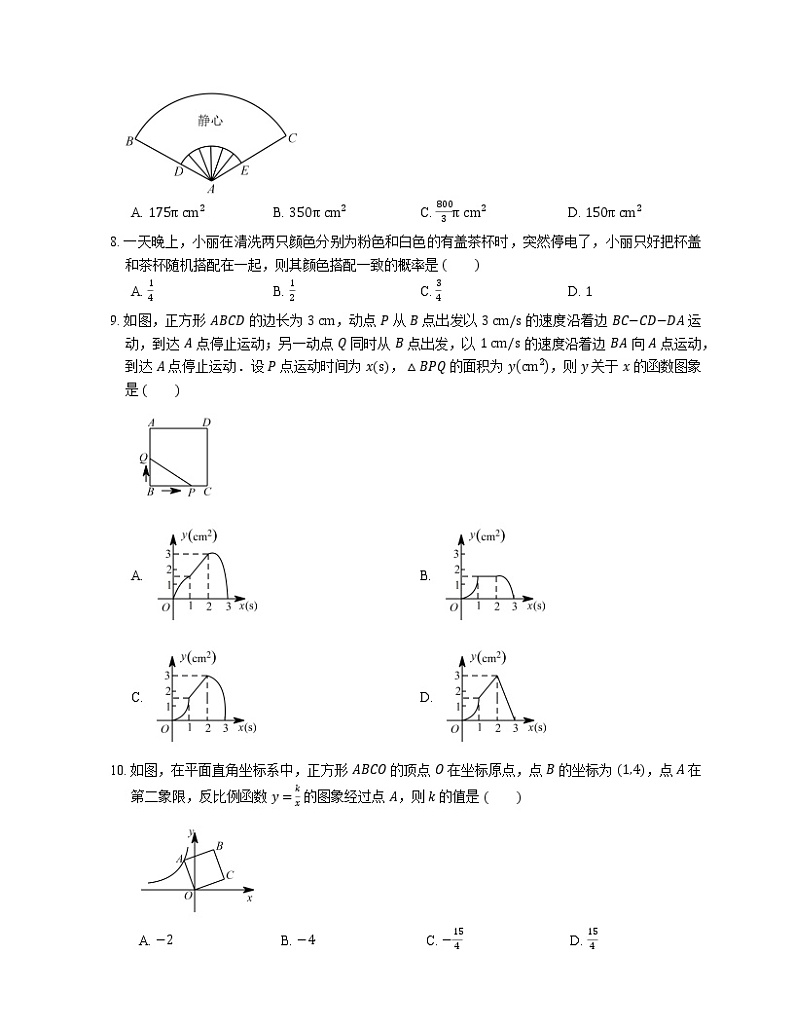
9. 如图，正方形 ABCD 的边长为 3 cm，动点 P 从 B 点出发以 3 cm/s 的速度沿着边 BC−CD−DA 运动，到达 A 点停止运动；另一动点 Q 同时从 B 点出发，以 1 cm/s 的速度沿着边 BA 向 A 点运动，到达 A 点停止运动．设 P 点运动时间为 xs，△BPQ 的面积为 ycm2，则 y 关于 x 的函数图象是
A. B.
C. D.

10. 如图，在平面直角坐标系中，正方形 ABCO 的顶点 O 在坐标原点，点 B 的坐标为 1,4，点 A 在第二象限，反比例函数 y=kx 的图象经过点 A，则 k 的值是
A. −2B. −4C. −154D. 154

二、填空题（共8小题；共40分）
11. 若把二次函数 y=x2+6x+2 化为 y=x−h2+k 的形式，其中 h，k 为常数，则 h+k= ．

12. 已知点 −1,y1，2,y2，3,y3 在反比例函数 y=−k2−1x 的图象上，则用“<”连接 y1，y2，y3 的结果为 ．

13. 如图是一个能自由转动的正六边形转盘，这个转盘被三条分割线分成形状相同，面积相等的三部分，且分别标为“1”“2”“3”三个数字，指针的位置固定不动．让转盘自由转动两次，当每次转盘停止后，记录指针指向的数（当指针指向分割线时，视其指向分割线左边的区域），则两次指针指向的数都是奇数的概率为 ．

14. 在一个不透明的布袋中有除颜色外其它都相同的红、黄、蓝球共 200 个，某位同学经过多次摸球试验后发现，其中摸到红色球和蓝色球的频率稳定在 35% 和 55%，则口袋中可能有黄球 个．

15. 如图，在平行四边形 ABCD 中，E 是边 BC 上的点，分别连接 AE，BD，二者相交于点 O，若 AD=5，BODO=35，则 EC= ．

16. 已知正六边形 ABCDEF 的边心距为 3 cm，则正六边形的半径为 cm．

17. 一个不透明的盒子里有 4 个除所标数字外其他完全相同的小球，小球上分别标有 1，−1，−2，−3 四个不同的数字，每次摸球前先将盒子里的球摇匀，任意摸出一个球记下数字后再放回盒子，那么两次摸出的小球上两个数字乘积是负数的概率为 ．

18. 如图，矩形 ABCD 中，AD=2，AB=5，P 为 CD 边上的动点，当 △ADP 与 △BCP 相似时，DP= ．

三、解答题（共6小题；共78分）
19. 反比例函数 y=2x 的图象与一次函数 y=kx+b 的图象交于点 Am,2，点 B−2,n, 一次函数图象与 y 轴的交点为 C，连接 AO．
（1）求一次函数的解析式；
（2）求 △AOC 的面积．

20. 如图，D 是 △ABC 的边 AB 上一点，连接 CD，若 AD=2，BD=4，∠ACD=∠B，求 AC 的长．

21. 如图，点 O 为 Rt△ABC 斜边 AB 上的一点，以 OA 为半径的 ⊙O 与 BC 切于点 D，与 AC 交于点 E，连接 AD．
（1）求证：AD 平分 ∠BAC；
（2）若 ∠BAC=60∘，OA=2，求阴影部分的面积（结果保留 π）．

22. 如图，甲、乙分别是 4 等分、 3 等分的两个圆转盘，指针固定，转盘转动停止后，指针指向某一数字．
（1）直接写出转动甲盘停止后指针指向数字“1”的概率；
（2）小华和小明利用这两个转盘做游戏，两人分别同时转动甲、乙两个转盘，停止后，指针各指向一个数字，若两数字之积为非负数则小华胜；否则，小明胜．你认为这个游戏公平吗?请你利用列举法说明理由．

23. 如图，在 △ABC 中，AB=8 cm，BC=16 cm，点 P 从点 A 出发沿 AB 边向点 B 以 2 cm/s 的速度移动，点 Q 从点 B 出发沿 BC 边向点 C 以 4 cm/s 的速度移动，如果 P，Q 同时出发，经过几秒后 △PBQ 和 △ABC 相似?

24. 如图，直线 y=12x+2 分别交 x 轴，y 轴于点 A，C，点 P 是该直线与反比例函数在第一象限内的一个交点，PB⊥x 轴于点 B，且 S△ABP=9．
（1）求证：△AOC∽△ABP；
（2）求点 P 的坐标；
（3）设点 R 与点 P 在同一反比例函数的图象上，且点 R 在直线 PB 的右侧，作 RT⊥x 轴于点 T，当 △BRT 与 △AOC 相似时，求点 R 的坐标．
答案
第一部分
1. B
2. C
3. C
4. A
5. B
【解析】∵−a2−1<0，
∴ 反比例函数图象位于二、四象限，在每个象限内，y 随 x 的增大而增大，
∵x1<0 ∴y26. A【解析】设宽为 x cm，
则 x20=5−12，
解得 x≈12.36．
7. B【解析】由题意得 贴纸部分的面积=2×120π×252360−120π×25−152360=350π cm2．
8. B
9. C
10. C
第二部分
11. −10
12. y213. 49
【解析】本题考查求概率．
根据题意，列表如下：
由表中可以得出，转盘自由转动两次共有 9 种等可能结果，其中两次都指向奇数的有 4 种，
故 P两次都指向奇数=49．
14. 20
15. 2
16. 2
【解析】如图所示，
连接 OA，OB，过 O 作 OG⊥AB，
∵ 多边形 ABCDEF 是正六边形，
∴∠OAG=60∘，
∴OG=OA⋅sin∠OAB=32AO=3，解得 AO=2．
17. 38
18. 1 或 4 或 2.5
第三部分
19. （1） ∵ 反比例函数 y=2x 的图象经过点 Am,2，点 B−2,n，
∴m=1，n=−1，
∵y=kx+b 经过点 A1,2，B−2,−1，
∴k+b=2,−2k+b=−1.
∴k=1,b=1.
∴ 一次函数解析式为 y=x+1．
（2） 当 x=0 时，y=1，
∴ 点 C 的坐标为 0,1．
∵ 一次函数 y=x+1 交 y 轴于 C0,1，
∴S△AOC=12×1×1=12．
20. 在 △ABC 和 △ACD 中，
∵∠ACD=∠B，∠A=∠A，
∴△ABC∽△ACD．
∴ACAB=ADAC，即 AC2=AD⋅AB=AD⋅AD+BD=2×6=12．
∴AC=23．
21. （1）
如图，连接 OD．
∵BC 是 ⊙O 的切线，D 为切点，
∴OD⊥BC．
又 AC⊥BC，
∴OD∥AC，
∴∠ADO=∠CAD．
又 OD=OA，
∴∠ADO=∠OAD，
∴∠CAD=∠OAD，即 AD 平分 ∠BAC．
（2）
如图，连接 OE，ED．
∵∠BAC=60∘，OE=OA，
∴△OAE 为等边三角形，
∴∠AOE=60∘，
∴∠ADE=30∘．
又 ∠OAD=12∠BAC=30∘，
∴∠ADE=∠OAD，
∴ED∥AO，
∴S△AED=S△OED，
∴ 阴影部分的面积为 S扇形ODE=60×π×4360=23π．
22. （1） 甲盘停止后指针指向数字“1”的概率 =14；
（2） 不公平．理由如下：
列表枚举所有情况如下表：
∵ 由两个转盘各转出一数字作积的所有可能情况有 12 种，每种情况出现的可能性相同，其中两个数字之积为非负数的有 7 个，为负数的有 5 个，
∴P小华获胜=712，P小明获胜=512．
∴ 这个游戏不公平．
23. 设经过 x 秒后 △PBQ 和 △ABC 相似．
则 AP=2x cm，BQ=4x cm，
∵ AB=8 cm，
∴ BP=8−2xcm，
①若 △BPQ∽△BCA，则 BPBC=BQAB，
即 8−2x16=4x8，
解得 x=0.8，
②若 △BPQ∽△BAC，则 BPAB=BQBC，
即 8−2x8=4x16，
解得 x=2．
综上所述，经过 0.8 秒或 2 秒后 △PBQ 和 △ABC 相似．
24. （1） ∵ PB⊥x轴，
∴ ∠ABP=90∘，
∵ ∠CAO=∠PAB，∠AOC=∠ABP=90∘，
∴ △AOC∽△ABP．
（2） 设 Aa,0，C0,c，由题意得 12a+2=0,c=2, 解得：a=−4,c=2,
∴ A−4,0，C0,2，即 AO=4，OC=2，
∵ S△ABP=9，
∴ AB⋅BP=18，
∵ △AOC∽△ABP，
∴ AOAB=OCBP，即 4AB=2BP，
∴ 2BP=AB，
∴ 2BP2=18，
∴ BP2=9，
∴ BP=3，
∴ AB=6，
∴ OB=2，
∴ P 点坐标为 2,3．
（3） 设反比例函数的解析式为 y=kx，将 P2,3 代入，
得 k2=3，解得 k=6，
∴ 反比例函数的解析式为 y=6x，
设 R 点的坐标为 x,y，
当 △BTR∽△AOC 时，
AOOC=BTRT，即 42=x−2y，
∴ 2y=x−2，
∴ y=6x,2y=x−2, 解得：x=13+1,y=13−12 或 x=1−13,y=−1−132（不合题意，舍去），
此时点 R 的坐标为 13+1,13−12；
当 △BTR∽△COA 时，
AOOC=RTBT，即 42=yx−2，
∴ y=2x−4，
∴ y=6x,y=2x−4,
解得：x=3,y=2 或 x=−1,y=−6（不合题意，舍去），
∴ 点 R 的坐标为 3,2，
综上所述，点 R 的坐标为 13+1,13−12 或 3,2．