2018-2019学年天津市河北区九上期末数学试卷

这是一份2018-2019学年天津市河北区九上期末数学试卷，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 如图，⊙O 是正五边形 ABCDE 的外接圆，则正五边形的中心角 ∠AOB 的度数是
A. 72∘B. 60∘C. 54∘D. 36∘

2. 有一条弧的长为 2π cm，半径为 2 cm，则这条弧所对的圆心角的度数是
A. 90∘B. 120∘C. 180∘D. 135∘

3. 下列事件是必然事件的是
A. n 边形的每个内角都相等B. 同位角相等
C. 分式方程有增根D. 三角形内角和等于 180∘

4. 用 2，3，4 三个数字排成一个三位数，则排出的数是偶数的概率为
A. 12B. 14C. 35D. 23

5. 如图，点 P 是平行四边形 ABCD 边 AB 上的一点，射线 CP 交 DA 的延长线于点 E，则图中相似的三角形有
A. 0 对B. 1 对C. 2 对D. 3 对

6. 如图，在 △ABC 中，D，E 分别是 AB 和 AC 上的点，且 DE∥BC，AEEC=52，DE=10，则 BC 的长为
A. 16B. 14C. 12D. 11

7. 已知点 A−2,y1，B3,y2 是反比例函数 y=kxk<0 图象上的两点，则有
A. y1<0
8. 函数 y=ax2−a 与 y=axa≠0 在同一直角坐标系中的图象可能是
A. B.
C. D.

9. 对于反比例函数 y=kxk≠0，下列所给的四个结论中，正确的是
A. 若点 2,4 在其图象上，则 −2,4 也在其图象上
B. 当 k>0 时，y 随 x 的增大而减小
C. 过图象上任一点 P 作 x 轴、 y 轴的垂线，垂足分别 A，B，则矩形 OAPB 的面积为 k
D. 反比例函数的图象关于直线 y=x 和 y=−x 成轴对称

10. 如图，D 是等边 △ABC 边 AB 上一点，且 AD:DB=1:2，现将 △ABC 折叠，使点 C 与 D 重合，折痕为 EF，点 E，F 分别在 AC 和 BC 上，则 CE:CF=
A. 34B. 45C. 56D. 67

二、填空题（共7小题；共35分）
11. 正六边形的外接圆的半径与内切圆的半径之比为 ．

12. 若 △ABC∽△AʹBʹCʹ，且 △ABC 与 △AʹBʹCʹ 的面积之比为 1:3，则相似比为 ．

13. 在一个不透明的口袋中装有 5 个红球和若干个白球，它们除颜色外其他完全相同，通过多次摸球实验后发现，摸到红球的频率稳定在 0.25 附近，则估计口袋中白球大约有 个．

14. 已知圆锥的底面圆半径为 3，母线长为 5，则圆锥的全面积是 ．

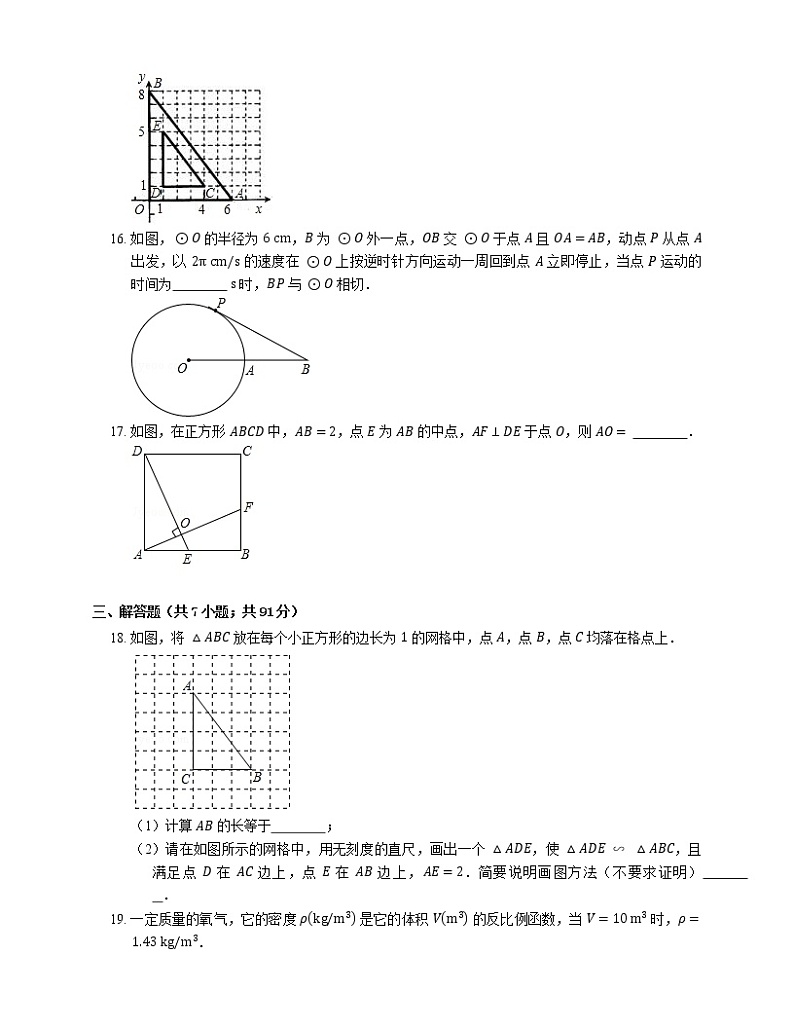
15. 如图，在平面直角坐标系中，已知点 O0,0，A6,0，B0,8，以某点为位似中心，作出 △AOB 的位似 △CDE，则位似中心的坐标为

16. 如图，⊙O 的半径为 6 cm，B 为 ⊙O 外一点，OB 交 ⊙O 于点 A 且 OA=AB，动点 P 从点 A 出发，以 2π cm/s 的速度在 ⊙O 上按逆时针方向运动一周回到点 A 立即停止，当点 P 运动的时间为 s 时，BP 与 ⊙O 相切．

17. 如图，在正方形 ABCD 中，AB=2，点 E 为 AB 的中点，AF⊥DE 于点 O，则 AO= ．

三、解答题（共7小题；共91分）
18. 如图，将 △ABC 放在每个小正方形的边长为 1 的网格中，点 A，点 B，点 C 均落在格点上．
（1）计算 AB 的长等于 ；
（2）请在如图所示的网格中，用无刻度的直尺，画出一个 △ADE，使 △ADE∽△ABC，且满足点 D 在 AC 边上，点 E 在 AB 边上，AE=2．简要说明画图方法（不要求证明） ．

19. 一定质量的氧气，它的密度 ρkg/m3 是它的体积 Vm3 的反比例函数，当 V=10 m3 时，ρ=1.43 kg/m3．
（1）求 ρ 与 V 的函数关系式；
（2）当 V=2 m3 时，求氧气的密度 ρ．

20. 现有两组相同的扑克牌，每组两张，两张牌的牌面数字分别是 2 和 3，从每组牌中各随机摸出一张牌，称为一次试验．
（1）小红与小明用一次试验做游戏，如果摸到的牌面数字相同小红获胜，否则小明获胜，请用列表法或画树状图的方法说明这个游戏是否公平?
（2）小丽认为：“在一次试验中，两张牌的牌面数字和可能为 4 、 5 、 6 三种情况，所以出现'和为 4 '的概率是 13 ”，她的这种看法是否正确?说明理由．

21. 如图，为了计算河两岸间的宽度，我们在河对岸的岸边选定一个目标作为点 A，再在河岸的这一边选点 B 和点 C，使 AB⊥BC，然后再选点 E，使 EC⊥BC，BC 与 AE 的交点为 D．测得 BD=120 米，DC=60 米，EC=50 米，请求出两岸之间 AB 的距离．

22. 如图，AB⊥BC，DC⊥BC，E 是 BC 上一点，且 AE⊥DE．
（1）求证：△ABE∽△ECD；
（2）若 AB=4，AE=BC=5，求 ED 的长．

23. 如图，在 △ABC 中，∠C=90∘，AB=10，AC=8，将线段 AB 绕点 A 按逆时针方向旋转 90∘ 到线段 AD．△EFG 由 △ABC 沿 CB 方向平移得到，且直线 EF 过点 D．
（1）求 ∠1 的大小；
（2）求 AE 的长．

24. 如图，在平面直角坐标系 xOy 中，反比例函数 y=mx 的图象与一次函数 y=kx−2 的图象交点为 A3,2，Bx,y．
（1）求反比例函数与一次函数的解析式及 B 点坐标；
（2）若 C 是 y 轴上的点，且满足 △ABC 的面积为 10，求 C 点坐标．
答案
第一部分
1. A【解析】∵⊙O 是正五边形 ABCDE 的外接圆，
∴∠AOB=360∘÷5=72∘．
2. C【解析】由题意得，2π=nπ×2180，解得：n=180．
即这条弧所对的圆心角的度数是 180∘．
3. D【解析】A．n 边形的每个内角都相等是随机事件；
B．同位角相等是随机事件；
C．分式方程有增根是随机事件；
D．三角形内角和等于 180∘ 是必然事件．
4. D【解析】∵ 用 2，3，4 三个数字排成一个三位数，等可能的结果有：234，243，324，342，423，432，
∵ 排出的数是偶数的有：234，324，342，432，
∴ 排出的数是偶数的概率为：46=23．
5. D
【解析】∵ 四边形 ABCD 是平行四边形，
∴AB∥DC，AD∥BC，
∴△EAP∽△EDC，△EAP∽△CBP，
∴△EDC∽△CBP，故有 3 对相似三角形．
6. B【解析】∵AEEC=52，
∴AEAC=57，
∵DE∥BC，
∴△ADE∽△ABC，
∴AEAC=DEBC，
∴57=10BC，
∴BC=14．
7. B【解析】∵ 反比例函数 y=kxk<0 中，k<0，
∴ 此函数图象在二、四象限，
∵−2<0，
∴ 点 A−2,y1 在第二象限，
∴y1>0，
∵3>0，
∴B3,y2 点在第四象限，
∴y2<0，
∴y1，y2 的大小关系为 y2<08. A【解析】当 a>0 时，函数 y=ax2−a 的图象开口向上，但当 x=0 时，y=−a<0，故B不可能；
当 a<0 时，函数 y=ax2−a 的图象开口向下，但当 x=0 时，y=−a>0，故C，D不可能．
可能的是A．
9. D【解析】A．若点 2,4 在其图象上，则 −2,4 不在其图象上，故本选项不符合题意；
B．当 k>0 时，y 随 x 的增大而减小，错误，应该是当 k>0 时，在每个象限，y 随 x 的增大而减小，故本选项不符合题意；
C．错误，应该是过图象上任一点 P 作 x 轴、 y 轴的线，垂足分别 A，B，则矩形 OAPB 的面积为 k，故本选项不符合题意；
D．正确，本选项符合题意．
10. B
【解析】解法一：设 AD=k，则 DB=2k，
∵△ABC 为等边三角形，
∴AB=AC=3k，∠A=∠B=∠C=∠EDF=60∘，
∴∠EDA+∠FDB=120∘，
又 ∠EDA+∠AED=120∘，
∴∠FDB=∠AED，
∴△AED∽△BDF，
∴EDFD=ADBF=AEBD．
设 CE=x，则 ED=x，AE=3k−x，
设 CF=y，则 DF=y，FB=3k−y，
∴xy=k3k−y=3k−x2k，
∴ky=x3k−y,2kx=y3k−x,
∴xy=45，
∴CE:CF=4:5．
解法二：设 AD=k，则 DB=2k，
∵△ABC 为等边三角形，
∴AB=AC=3k，∠A=∠B=∠C=∠EDF=60∘，
∴∠EDA+∠FDB=120∘，
又 ∠EDA+∠AED=120∘，
∴∠FDB=∠AED，
∴△AED∽△BDF，由折叠，得 CE=DE，CF=DF，
∴△AED 的周长为 4k，△BDF 的周长为 5k，
∴△AED 与 △BDF 的相似比为 4:5，
∴CE:CF=DE:DF=4:5．
第二部分
11. 2:3
【解析】设正六边形的半径是 r，则外接圆的半径 r，
内切圆的半径是正六边形的边心距，因而是 32r，
因而正六边形的外接圆的半径与内切圆的半径之比为 2:3．
12. 1:3
【解析】∵△ABC∽△AʹBʹCʹ，△ABC 与 △AʹBʹCʹ 的面积之比为 1:3，
∴△ABC 与 △AʹBʹCʹ 的相似比为 1:3．
13. 15
【解析】设白球个数为 x 个，
∵ 摸到红色球的频率稳定在 0.25 左右，
∴ 口袋中得到红色球的概率为 0.25，
∴5x+5=14，解得：x=15，即白球的个数为 15 个．
14. 24π
【解析】底面周长是：2×3π=6π，
则侧面积是：12×6π×5=15π，
底面积是：π×32=9π，
则全面积是：15π+9π=24π．
15. 2,2
【解析】【分析】直接利用位似图形的性质得出位似中心．
【解析】解：如图所示，点 P 即为位似中点，其坐标为 2,2，
故答案为：2,2．
【点评】此题主要考查了位似变换，正确掌握位似中心的定义是解题关键．
16. 1 或 5
【解析】连接 OP．
∵ 直线 BP 与 ⊙O 相切，
∴∠OPB=90∘，
∵AB=OA=OP，
∴OB=2OP，
∴∠PBO=30∘，
∴POB=60∘，
∴ 弧 AP 的长是 60⋅π⋅6180=2π，即时间是 2π÷2π=1（秒）；
当在 Pʹ 点时，直线 BP 与 ⊙O 相切，
此时优弧 APPʹ 的长是 360−60⋅π⋅6180=10π，即时间是 10π÷2π=5（秒）．
17. 255
【解析】∵ 四边形 ABCD 是正方形，
∴AD=BC=2，∠DAE=90∘，
∵AE=EB=1，
∴DE=22+12=5，
∵AO⊥DE，
∴12×DE×AO=12×AE×AD，
∴AO=255．
第三部分
18. （1） 5
【解析】AB=32+42=5．
（2） 取点 M，N，连接 MN 交 AC 于点 D，使得 ADCD=53，取点 P，连接 PC 交 AB 于点 E，使得 AEEB=23，连接 DE，△ADE 即为所求
19. （1） 设 ρ=kVk≠0，
∴1.43=k10，
∴k=14.3，
∴ρ=14.3V=14310V．
（2） 当 V=2 m3 时，ρ=14.32=7.15 kg/m3．
20. （1） 列表正确或树状图正确．
P小明获胜=P数字不同=12，
∵P小红获胜=P小明获胜，
∴ 这个游戏公平．
（2） 不正确．
因为“和为 4 ”只出现了一次，由列表或树状图可知和的情况总共有 4 种，故“和为 4 ”的概率应为 14．
21. ∵AB⊥BC，EC⊥BC，
∴∠ABC=∠BCE=90∘，
∵∠ADB=∠CDE，
∴△ABD∽△ECD，
∴ABCE=BDCD，即：AB50=12060，解得 AB=100．
答：两岸之间 AB 的距离为 100 米．
22. （1） ∵AB⊥BC，DC⊥BC，
∴∠B=∠C=90∘，∠BAE+∠AEB=90∘，
∵AE⊥DE，
∴∠AED=90∘，
∴∠AEB+∠DEC=90∘，
∴∠DEC=∠BAE，
∴△ABE∽△ECD．
（2） 在 Rt△ABE 中，
∵AB=4，AE=5，
∴BE=3，
∵BC=5，
∴EC=5−3=2，
由（1）得：△ABE∽△ECD，
∴ABAE=ECCD，
∴45=2DE，
∴DE=52．
23. （1） ∵ 线段 AD 是由线段 AB 绕点 A 按逆时针方向旋转 90∘ 得到，
∴∠DAB=90∘，AD=AB，
∴∠ABD=45∘，
∵△EFG 是 △ABC 沿 CB 方向平移得到，
∴AB∥EF，
∴∠1=∠ABD=45∘．
（2） 由平移的性质得，AE∥CG，AB∥EF，
∴∠DEA=∠DFC=∠ABC，∠ADE+∠DAB=180∘，
∵∠DAB=90∘，
∴∠ADE=90∘，
∵∠ACB=90∘，
∴∠ADE=∠ACB，
∴△ADE∽△ACB，
∴ADAC=AEAB，
∵AC=8，AB=AD=10，
∴AE=12.5．
24. （1） ∵ 点 A3,2 在反比例函数 y=mx 和一次函数 y=kx−2 上，
∴2=m3，2=k3−2，解得 m=6，k=2，
∴ 反比例函数解析式为 y=6x 和一次函数解析式为 y=2x−4；
∵ 点 B 是一次函数与反比例函数的另一个交点，
∴6x=2x−4，解得 x1=3，x2=−1，
∴B 点的坐标为 −1,−6．
（2）
∵ 点 M 是一次函数 y=2x−4 与 y 轴的交点，
∴ 点 M 的坐标为 0,−4，
设 C 点的坐标为 0,yC，
由题意知 12×3×yC−−4+12×1×yC−−4=10，
解得 yC+4=5．
当 yC+4≥0 时，yC+4=5，解得 yC=1；
当 yC+4≤0 时，yC+4=−5，解得 yC=−9，
∴ 点 C 的坐标为 0,1 或 0,−9．