2018年哈尔滨市平房区中考三模数学试卷

这是一份2018年哈尔滨市平房区中考三模数学试卷，共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. −7 的倒数是
A. 7B. −7C. 17D. −17

2. 下列运算结果为 a6 的是
A. a2+a3B. a2⋅a3C. −a23D. a8÷a2

3. 下列图形中，是中心对称图形，但不是轴对称图形的是
A. B.
C. D.

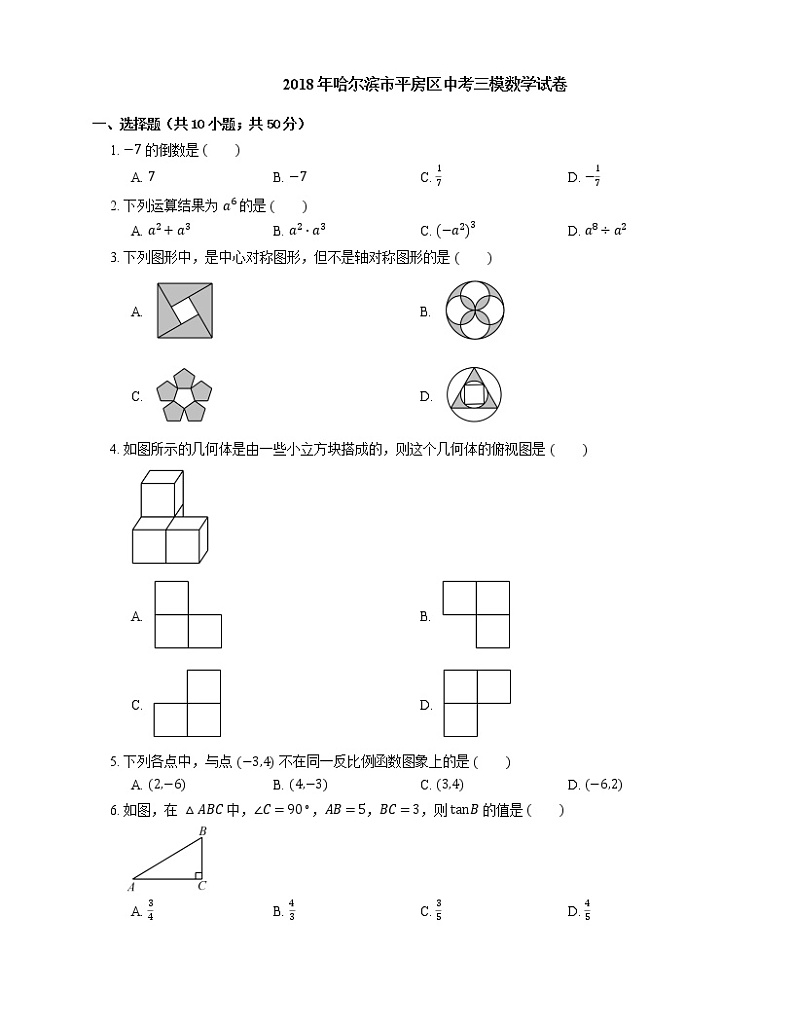
4. 如图所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是
A. B.
C. D.

5. 下列各点中，与点 −3,4 不在同一反比例函数图象上的是
A. 2,−6B. 4,−3C. 3,4D. −6,2

6. 如图，在 △ABC 中，∠C=90∘，AB=5，BC=3，则 tanB 的值是
A. 34B. 43C. 35D. 45

7. 我们定义一种新运算 a⊕b=a+ba−b，例如 5⊕2=5+25−2=73，则式子 7⊕−3 的值为
A. 15B. 25C. −15D. −25

8. 如图，在平行四边形 ABCD 中，点 E 在 AD 边上，CE，BA 的延长线交于点 F，下列结论错误的是
A. AFFE=ABCEB. CEEF=DEAEC. EFCF=AFABD. AEAD=EFCF

9. 如图，将一个矩形纸片 ABCD，沿着 BE 折叠，使 C，D 两点分别落在点 C1，D1 处．若 ∠C1BA=50∘，则 ∠ABE 的度数为
A. 10∘B. 20∘C. 30∘D. 40∘

10. 已知二次函数 y=ax2+bx+c 的部分图象如图所示，若连接该函数与坐标轴的交点所得到的三角形面积为 20，则该函数的最大值为
A. 133B. 143C. 5D. 163

二、填空题（共10小题；共50分）
11. 将 670000 用科学记数法表示为 ．

12. 计算：−18+2= ．

13. 在函数 y=4x2x−3 中，自变量 x 的取值范围是 ．

14. 因式分解：4ax2−16axy+16ay2= ．

15. 不等式组 x+2<3,−2x<4 的非负整数解为 ．

16. 一个扇形的面积是 12π cm2，圆心角是 60∘，则此扇形的半径是 cm．

17. 某工厂三月份的利润为 16 万元，五月份的利润为 25 万元，则平均每月利润的增长的百分率为 ．

18. 李老师想从小明、小红、小丽和小亮四个人中用抽签的方式抽取两个人做流动值周生，则小红和小丽同时被抽中的概率是 ．

19. 已知：在 △ABC 中，AH⊥BC，垂足为点 H，若 AB+BH=CH，∠ABH=70∘，则 ∠BAC= ．

20. 在 Rt△ABC 中，AB=AC=17，点 D 在 BC 上，点 E 在直线 BC 的下方，连接 AD，DE，BE，CE，若 CE∥AB，CEAD=413，∠CDE=12∠BAD，则 CD= ．

三、解答题（共7小题；共91分）
21. 先化简，再求代数式 2a+1+a+2a2−1÷3aa−1 的值，其中 a=tan60∘−2cs45∘．

22. 如图，方格纸中每个小正方形的边长均为 1，线段 AB 的两个端点在小正方形的顶点上．
（1）在图中画一个以 AB 为腰的等腰三角形 △ABE，点 E 在小正方形的顶点上，且 △ABE 的面积为 152；
（2）在图中画一个等腰三角形 △ABF，点 F 在小正方形的顶点上，且 tan∠AFB=12，连接 EF，请直接写出线段 EF 的长．

23. 为贯彻落实十九大会议精神，践行“绿水青山就是金山银山”的发展理念，积极推动生态文明理念融入学校教育，某中学拟举办“爱家乡、览名山”活动，围绕“哈尔滨市周边五大名山，即：香炉山、凤凰山、金龙山、帽儿山、二龙山，你最喜欢那一座山?（每名学生必选且只选一座山）”的问题在全校范围内随机抽取了部分学生进行问卷调查，根据调查结果绘制了如图所示的不完整统计图．请根据统计图的信息回答下列问题：
（1）本次调查共抽取了多少名学生?
（2）求本次调查中，最喜欢风凰山的学生人数，并补全条形统计图；
（3）若该中学共有学生 1200 名，请你估计该中学最喜欢香炉山的学生约有多少名．

24. 已知：如图，在 Rt△ABC 中，∠ACB=90∘，点 D，E 分别是 AB，AC 的中点，点 F 在 BC 延长线上，连接 EF，且 ∠CEF=∠BAC．
（1）如图 1，求证：四边形 CDEF 是平行四边形；
（2）如图 2，连接 AF，BE，在不添加任何辅助线的情况下，请直接写出图 2 中所有与 △AED 面积相等的三角形．

25. 某学校为了增强学生体质，开设了体育活动小组，并计划购买一些篮球和排球．已知每个篮球的售价比每个排球的售价多 20 元，用 1100 元购进的篮球数量是用 450 元购进排球数量的 2 倍．
（1）求每个篮球和每个排球的单价各是多少元；
（2）若学校计划购进篮球和排球共 50 个，且购进的总费用不超过 4900 元，则学校最多可以购进篮球多少个?

26. 已知：PA 是 ⊙O 的切线，点 B 在 ⊙O 上，连接 OB，OP，连接 AB 交 OP 于点 C，∠OBA=∠OPA．
（1）如图 1，求证：AC=BC；
（2）如图 2，OP 交 ⊙O 于点 D，过点 D 作 DF∥AP 交 AB 于点 E，连接 OE，求证：∠CED=2∠COE；
（3）如图 3，在（2）的条件下，延长 PO 交 ⊙O 于点 N，连接 AN 交 DF 于点 M，连接 OM，EP，若 ∠MOE=45∘，S△EDP=52，求线段 BE 的长．

27. 已知：在平面直角坐标系 xOy 中，直线 y=−x+3 分别交 x，y 轴于点 A，C，点 B 在 x 轴负半轴上，过点 A 作 AK⊥BC 于点 K，若 sin∠ABC=55，AK=955．
（1）如图 1，求点 B 坐标；
（2）如图 2，点 P 为 AC 延长线上一点，过点 P 作 PQ∥AB 交直线 BC 于点 Q，设点 P 的横坐标为 t，PQ 长为 d，求 d 与 t 的函数关系式（不必写出自变量 t 的取值范围）；
（3）在（2）的条件下，连接 OK，过点 P 作 PH⊥x 轴于点 H，点 F 为 HB 上一点，连接 PF，点 D 在 PF 上，将点 F 沿 x 轴正方向平移 d2 个单位到点 G，连接 DG，交 PH 于点 E，若 GE=AK，∠FDG=∠AKO，EH=PE+FH，求点 P 坐标．
答案
第一部分
1. D
2. D
3. A【解析】A、不是轴对称图形，是中心对称图形，故此选项正确；
B、是轴对称图形，也是中心对称图形，故此选项错误；
C、是轴对称图形，不是中心对称图形，故此选项错误；
D、是轴对称图形，不是中心对称图形，故此选项错误．
4. A【解析】从几何体上面看，是左边 2 个，右边 1 个正方形．
5. C
【解析】∵−3×4=2×−6=4×−3=−6×2=−12，3×4≠−12，
∴ 点 2,−6，4,−3，−6,2 和 −3,4 在反比例函数 y=−12x 的图象上，而点 3,4 不在反比例函数 y=−12x 的图象上．
6. B【解析】在 △ABC 中，
∵∠C=90∘，AB=5，BC=3，
∴AC=AB2−BC2=52−32=4，则 tanB=ACBC=43．
7. B【解析】根据题中的新定义得：7⊕−3=7+−37−−3=25．
8. C【解析】∵ 四边形 ABCD 是平行四边形，
∴AB∥CD，AB=CD，AD∥BC，AD=BC，
∴△AEF∽△BCF，△AEF∽△DEC，
∴AFFE=ABCE，CEEF=DEAE，AEAD=EFCF=AFBF．
9. B【解析】设 ∠ABE=x，根据折叠前后角相等可知，∠C1BE=∠CBE=50∘+x，
∵∠ABC=90∘，
∴50∘+x+x=90∘，解得 x=20∘．
10. D
【解析】∵ 抛物线与 x 轴的一个交点坐标为 3,0，对称轴为直线 x=−1，
∴ 抛物线与 x 轴另一交点坐标为 −5,0，
∴S=12×3−−5c=20，
∴c=5．
将点 −5,0，3,0 代入 y=ax2+bx+5，
得：25a−5b+5=0,9a+3b+5=0, 解得：a=−13,b=−23,
∴ 抛物线的解析式为 y=−13x2−23x+5=−13x+12+163，
∴ 该函数的最大值为 163．
第二部分
11. 6.7×105
12. −22
13. x≠32
【解析】函数 y=4x2x−3 中，2x−3≠0，解得 x≠32．
14. 4ax−2y2
【解析】原式=4ax2−4xy+4y2=4ax−2y2．
15. x=0
【解析】解不等式 x+2<3，得：x<1，
解不等式 −2x<4，得：x>−2，
则不等式组的解集为 −2 ∴ 不等式组的非负整数解为 x=0．
16. 62
17. 25%
【解析】设该工厂平均每月利润增长的百分率是 x，
依题意得：161+x2=25，
∴1+x=±1.25，
∴x1=0.25=25%，x2=−2.25（负值舍去）．
即该工厂平均每月利润增长的百分率是 25%．
18. 16
【解析】画树状图如图所示：
∵ 共有 12 种等可能的结果，小红和小丽同时被抽中的有 2 种情况，
∴ 小红和小丽同时被抽中的概率是：212=16．
19. 75∘ 或 35∘
【解析】当 ∠ABC 为锐角时，过点 A 作 AD=AB，交 BC 于点 D，如图 1 所示．
∵AB=AD，
∴∠ADB=∠ABH=70∘，BH=DH．
∵AB+BH=CH，CH=CD+DH，
∴CD=AB=AD，
∴∠C=12∠ADB=35∘，
∴∠BAC=180∘−∠ABH−∠C=75∘．
当 ∠ABC 为钝角时，如图 2 所示．
∵AB+BH=CH，
∴AB=BC，
∴∠BAC=∠ACB=12∠ABH=35∘．
20. 122
【解析】如图，延长 AD，CE 交于 G 点，作 AH⊥BC 于 H，在 CG 上截取 CF=AC，
∵AB=AC=17，∠BAC=90∘，
∴∠ABC=∠ACB=45∘．
∵AB∥CE，
∴∠ABC=∠BCG=45∘，
∴∠ACB=∠BCG，
在 △ADC 和 △FDC 中，
CD=DC,∠ACD=∠FCD,AC=FC,
∴△ADC≌△FDC，
∴DF=AD，∠ADC=∠CDF．
∵CEAD=413，
∴ 设 AD=13a=DF，CE=4a，
设 ∠CDE=x∘，则 ∠BAD=2x∘，
∵∠ADC=∠ABC+∠BAD=45∘+2x∘，
∴∠CDF=45∘+2x∘，
∴∠EDF=45∘+x∘，且 ∠DEF=∠CDE+∠DCE=45∘+x∘，
∴∠FDE=∠DEF，
∴DF=EF=13a．
∵CF=EF+CE=13a+4a=17，
∴a=1，
∴AD=13，CE=4．
在 Rt△AHC 中，AC=17，∠ACH=45∘，
∴AH=CH=1722，
在 Rt△ADH 中，DH=AD2−AH2=722，
∴CD=DH+CH=122．
第三部分
21. 原式=2a−2a+1a−1+a+2a+1a−1⋅a−13a=3aa+1a−1⋅a−13a=1a+1,
∵a=tan60∘−2cs45∘=3−2×22=3−1,
∴原式=13−1+1=13=33.
22. （1） 如图所示，△ABE 即为所求．
（2） 如图所示，△ABF 即为所求；在 Rt△BEF 中，EF=52+52=52．
23. （1） 20÷25%=80（名），
答：本次调查共抽取了 80 名学生．
（2） 补全的条形统计图如图所示：
（3） 1200×2480=360（名），
答：估计该中学最喜欢香炉山的学生约有 360 名．
24. （1） 如图 1
∵ 点 D，E 分别是 AB，AC 的中点，
∴ DE 是 △ABC 的中位线，
∴ DE∥BC，
∵ ∠ACB=90∘，AD=DB，
∴ CD=AD=DB，
∴ ∠A=∠DCA，
∵ ∠CEF=∠A，
∴ ∠CEF=∠ECD，
∴ EF∥CD，
∴ 四边形 CDEF 是平行四边形．
（2） 如图 2 中，与 △AED 面积相等的三角形有：△AEF，△ECF，△EDC，△EDB．
理由：∵ 四边形 CDEF 是平行四边形，
∴ △EFC 与 △DEC 的面积相等，
∵ AE=EC，DE∥BC，
∴ △ADE 与 △EDC，△EDC 与 △EDB 的面积相等，
∴ 与 △AED 面积相等的三角形有：△AEF，△ECF，△EDC，△EDB．
25. （1） 设每个篮球和每个排球的单价分别为 x 元，x−20 元，
根据题意可得：
1100x=2×450x−20.
解得：
x=110.
经检验 x=110 是原方程的解，并且满足题意．
所以
x−20=90.
答：每个篮球和每个排球的单价各是 110 元，90 元．
（2） 设购进篮球 a 个，排球 50−a 个，根据题意可得：
110a+9050−a≤4900.
解得：
a≤20.
答：学校最多可以购进篮球 20 个．
26. （1） 连接 OA，如图 1．
∵OA=OB，
∴∠OAB=∠OBA，
∵PA 是 ⊙O 的切线，
∴OA⊥AP，
∴∠OAB+∠BAP=90∘，
∵∠OBA=∠OPA，
∴∠OPA+∠BAP=90∘，
∴AB⊥OP，
∴AC=BC．
（2） 连接 OA 交 DF 于点 G，如图 2．
∵OA⊥AP，
∴∠OAP=90∘，
∵DF∥AP，
∴∠OGD=∠OAP=90∘，
∴∠GOD+∠ODG=90∘，
∵AB⊥OP，
∴∠CED+∠CDE=90∘，
∴∠GOD=∠CED，
在 △AOC 和 △DOG 中，
∠AOC=∠DOG,∠ACO=∠DGO,OA=OD,
∴△AOC≌△DOG，
∴OC=OG，
在 Rt△GOE 与 Rt△COE 中，
OE=OE,OG=OC,
∴Rt△GOE≌Rt△COE，
∴∠AOE=∠DOE，
∴∠GOD=2∠EOD，
∵∠GOD=∠CED，
∴∠CED=2∠EOD．
（3） 连接 AO，AD，作 OL⊥AN 于点 L，如图 3．
设 ∠EOC=α，则 ∠CED=2α，
∴∠MOD=45∘+α，∠EDC=90∘−2α，
∴∠OMD=180∘−∠MOD−∠EDC=45∘+α，
∴∠MOD=∠OMD，
∴OD=MD=ON，
∵OA⊥DF
∴AF=AD，
∴∠AND=∠ADF，
∵OL⊥AN，
∴∠OLN=90∘，
∵ND 是 ⊙O 的直径，
∴∠DAN=90∘，
在 △NOL 和 △DMA 中，
∠LNO=∠ADM,∠NLO=∠DAN,ON=MD,
∴△NOL≌△DMA，
∴OL=AM，
∵L 为 AN 的中点，O 为 ND 的中点，
∴LO 为 △AND 的中位线，
∴AD=2OL=2AM，
在 △AOE 和 △DOE 中，
AO=DO,∠AOE=∠DOE,OE=OE,
∴△AOE≌△DOE，
∴AE=DE，
∴∠EAD=∠EDA，
∵∠EAD+∠EAM=90∘，∠EDA+∠DMA=90∘，
∴∠AME=∠EAM，
∴EM=AE=ED，
∵S△EDP=12ED⋅AG=52，
∴S△AMD=12MD⋅AG=12AM⋅AD=5，
∴AM=5，AD=25，
∴MD=ON=OD=5，
∴tan∠CAD=tan∠ADM=AMAD=12，
在 Rt△ACD 中，设 CD=x，AC=2x，
由勾股定理可知：4x2+x2=20，解得：x1=2，x2=−2（舍去），
∴CD=2，AC=4，
∴AE=12MD=52，
∴CE=AC−CE=32，
∴BE=BC+CE=112．
27. （1） ∵AK⊥BC，
∴∠AKC=90∘，
在 Rt△ABK 中，AK=955，
∴sin∠ABC=AKAB=955AB=55
∴AB=9，
∵ 直线 y=−x+3 分别交 x，y 轴于点 A，C，
∴C0,3，A3,0，
∴OB=AB−OA=6，
∴B−6,0．
（2） ∵B−6,0，C0,3，
设直线 BC 的解析式为 y=k1x+b1，
∴0=−6k1+b1,3=b1,
解得：k1=12,b1=3.
∴ 直线 BC 的解析式为 y=12x+3，
∵ 点 P 为 AC 延长线上一点，
∴Pt,−t+3，
把 y=−t+3 代入 y=12x+3 得，x=−2t，
∴d=−2t−t=−3tt<0．
（3） 如图，过点 O 作 OM⊥OK 交 KA 延长线于点 M，
∴∠AOC=∠AKC=90∘，
∴∠KCO=∠OAM，
在 △OCK 和 △OAM 中 ∠KCO=∠MAO,∠KOC=∠MOA,OA=OC,
∴△OCK≌△OAM，
∴OK=OM，
∴∠OKM=∠FDG=45∘，
设 ∠DPE=α，
∴∠DEP=∠HEG=45∘−α，
∵PH⊥OB，
∴∠EGH=45∘+α，
在 FN 上取一点 N 作 NR⊥HB 与过点 E 作 ER⊥PH 交于点 R，
∴ 四边形 BHER 是矩形，连接 PR，
∵EH=PE+HF，
∴EH=NH，
∴ 矩形 BHER 是正方形，
∴ER=RN，
在 △REP 和 △RNF 中 ∠PRE=∠FRN,ER=RN,∠REP=∠RNF,
∴△REP≌△RNF，
∴RF=RP，PE=NF，
∴∠RPF=∠RFP=45∘，
在 △RNF 和 △EHG 中 ∠RFN=∠EGH,∠RNF=∠EHG,RN=EH,
∴△RNF≌△EHG，
∴FN=HG=PE，
∴EH=FG=12d=−32t，
∴PE=HG=PH−EH=3−t+32t=3+12t，EG=AK=955，
在 Rt△HEG 中，EH2+GH2=EG2，
∴−32t2+3+12t2=9552，
∴t1=65（舍去）或 t2=−125，
将 t=−125 代入 y=−x+3 中，得 y=275，
∴P−125,275．