2019年云南省昆明市盘龙区、禄劝县中考二模数学试卷

这是一份2019年云南省昆明市盘龙区、禄劝县中考二模数学试卷，共14页。试卷主要包含了填空题，选择题，解答题等内容，欢迎下载使用。

一、填空题（共6小题；共30分）
1. −1 的相反数是 ．

2. 分解因式：x3−2x2+x= ．

3. 通过画出多边形的对角线，可以把多边形内角和问题转化为三角形内角和问题．如果从某个多边形的一个顶点出发的对角线共有 2 条，那么该多边形的内角和是 度．

4. 如图，四边形 ABCD 内接于 ⊙O，∠BCD=120∘，则 ∠BOD= 度．

5. 若关于 x 的一元二次方程 kx2−2x−1=0 有两个不相等的实数根，则实数 k 的取值范围是 ．

6. 矩形 ABCD 中，AB=6，BC=8．点 P 在矩形 ABCD 的内部，点 E 在边 BC 上，满足 △PBE∽△DBC，若 △APD 是等腰三角形，则 PE 的长为 ．

二、选择题（共8小题；共40分）
7. 世界上最小的鸟是生活在古巴的吸蜜蜂鸟，它的质量约为 0.056 盎司．将 0.056 用科学记数法表示为
A. 5.6×10−1B. 5.6×10−2C. 5.6×10−3D. 0.56×10−1

8. 函数 y=11−x 的自变量 x 的取值范围是
A. x>1B. x≠1C. x<1D. x≤1

9. 下列运算正确的是
A. 2a2b−ba2=a2bB. a6÷a2=a3
C. ab23=a2b5D. a+22=a2+4

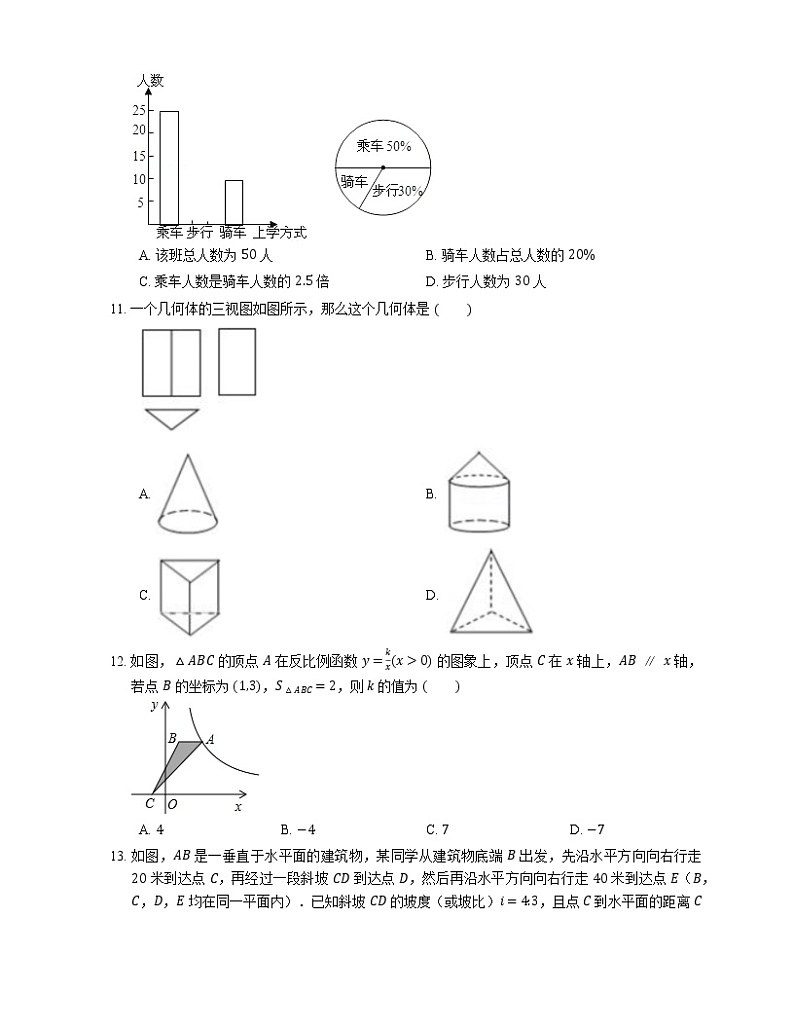
10. 下面两图是某班全体学生上学时，乘车，步行，骑车的人数分布条形统计图和扇形统计图（两图均不完整），则下列结论中错误的是
A. 该班总人数为 50 人B. 骑车人数占总人数的 20%
C. 乘车人数是骑车人数的 2.5 倍D. 步行人数为 30 人

11. 一个几何体的三视图如图所示，那么这个几何体是
A. B.
C. D.

12. 如图，△ABC 的顶点 A 在反比例函数 y=kxx>0 的图象上，顶点 C 在 x 轴上，AB∥x 轴，若点 B 的坐标为 1,3，S△ABC=2，则 k 的值为
A. 4B. −4C. 7D. −7

13. 如图，AB 是一垂直于水平面的建筑物，某同学从建筑物底端 B 出发，先沿水平方向向右行走 20 米到达点 C，再经过一段斜坡 CD 到达点 D，然后再沿水平方向向右行走 40 米到达点 E（B，C，D，E 均在同一平面内）．已知斜坡 CD 的坡度（或坡比）i=4:3，且点 C 到水平面的距离 CF 为 8 米，在 E 处测得建筑物顶端 A 的仰角为 24∘，则建筑物 AB 的高度约为 （参考数据：sin24∘=0.41，cs24∘=0.91，tan24∘=0.45）
A. 21.7 米B. 224 米C. 274 米D. 28.8 米

14. 如图，△ABC 中，∠ACB=90∘，AB=10，tanA=12．点 P 是斜边 AB 上一个动点．过点 P 作 PQ⊥AB，垂足为 P，交边 AC（或边 CB）于点 Q，设 AP=x，△APQ 的面积为 y，则 y 与 x 之间的函数图象大致为
A. B.
C. D.

三、解答题（共9小题；共117分）
15. 计算：3−8+π−20190−4cs30∘+−12．

16. 设 M=1a2−1÷1+1a−1．
（1）化简 M；
（2）当 a=1 时，记此时 M 的值为 f1=11×2=1−12；
当 a=2 时，记此时 M 的值为 f2=12×3=12−13；
当 a=3 时，记此时 M 的值为 f3=13×4=13−14；
⋯⋯
当 a=n 时，记此时 M 的值为 fn= ；
则 f1+f2+⋯+fn= ．
（3）解关于 x 的不等式组：x−22−2−x4≤f1+f2+f3,−x<1, 并将解集在数轴上表示出来．

17. 如图，以点 B 为圆心，适当长为半径画弧，交 BA 于点 D，交 BC 于点 E；分别以点 D，E 为圆心，大于 12DE 的长为半径画弧，两弧在 ∠ABC 的内部相交于点 F；画射线 BF，过点 F 作 FG⊥AB 于点 G，作 FH⊥BC 于点 H．
求证：BG=BH．

18. 某校七、八年级各有 10 名同学参加市级数学竞赛，各参赛选手的成绩如下（单位：分）：
七年级：89，92，92，92，93，95，95，96，98，98
八年级：88，93，93，93，94，94，95，95，97，98
整理得到如下统计表：
年级最高分平均分中位数众数方差七年级9894am7.6八年级98n94936.6
根据以上信息，完成下列问题：
（1）填空：a= ；m= ；n= ；
（2）两个年级中， 年级成绩更稳定；
（3）七年级两名最高分选手分别记为：A1，A2，八年级第一、第二名选手分别记为 B1，B2，现从这四人中，任意选取两人参加市级经验交流，请用树状图法或列表法求出这两人分别来自不同年级的概率．

19. 某水果店 5 月份购进甲、乙两种水果共花费 1700 元，其中甲种水果 8 元/千克，乙种水果 18 元/千克．6 月份，这两种水果的进价上调为：甲种水果 10 元/千克，乙种水果 20 元/千克．
（1）若该店 6 月份购进这两种水果的数量与 5 月份都相同，将多支付货款 300 元，求该店 5 月份购进甲、乙两种水果分别是多少千克?
（2）若 6 月份将这两种水果进货总量减少到 120 千克，且甲种水果不超过乙种水果的 3 倍，则 6 月份该店需要支付这两种水果的货款最少应是多少元?

20. 如图，PA 与 ⊙O 相切于点 A，过点 A 作 AB⊥OP，垂足为 C，交 ⊙O 于点 B．连接 PB，AO，并延长 AO 交 ⊙O 于点 D，与 PB 的延长线交于点 E．
（1）求证：PB 是 ⊙O 的切线；
（2）若 OC=3，AC=4，求 sin∠PAB 的值．

21. 某乡镇实施产业扶贫，帮助贫困户承包了荒山种植某品种蜜柚，到了收获季节，已知该蜜柚的成本价为 8 元/千克，投入市场销售时，调查市场行情，发现该蜜柚销售不会亏本，且每天销售量 y（千克）与销售单价 x（元/千克）之间的函数关系如图所示．
（1）求 y 与 x 的函数关系式，并写出 x 的取值范围；
（2）当该品种的蜜柚定价为多少时，每天销售获得的利润最大?最大利润是多少?
（3）某农户今年共采摘蜜柚 4800 千克，该品种蜜柚的保质期为 40 天，根据（2）中获得最大利润的方式进行销售，能否销售完这批蜜柚?请说明理由．

22. 如图 1 所示，在四边形 ABCD 中，点 O，E，F，G 分别是 AB，BC，CD，AD 的中点，连接 OE，EF，FG，GO，GE．
（1）证明：四边形 OEFG 是平行四边形；
（2）将 △OGE 绕点 O 顺时针旋转得到 △OMN，如图 2 所示，连接 GM，EN．
①若 OE=3，OG=1，求 ENGM 的值；
②试在四边形 ABCD 中添加一个条件，使 GM，EN 的长在旋转过程中始终相等．（不要求证明）

23. 如图①，已知抛物线 y=ax2−3ax−4aa<0 的图象与 x 轴交于 A，B 两点（A 在 B 的左侧），与 y 的正半轴交于点 C，连接 BC，二次函数的对称轴与 x 轴的交点 E．
（1）抛物线的对称轴与 x 轴的交点 E 坐标为 ，点 A 的坐标为 ；
（2）若以 E 为圆心的圆与 y 轴和直线 BC 都相切，试求出抛物线的解析式；
（3）在（2）的条件下，如图②，Qm,0 是 x 的正半轴上一点，过点 Q 作 y 轴的平行线，与直线 BC 交于点 M，与抛物线交于点 N，连接 CN，将 △CMN 沿 CN 翻折，M 的对应点为 Mʹ．在图②中探究：是否存在点 Q，使得 Mʹ 恰好落在 y 轴上?若存在，请求出 Q 的坐标；若不存在，请说明理由．
答案
第一部分
1. 1
【解析】根据相反数的定义，得 −1 的相反数是 1．
2. xx−12
【解析】x3−2x2+x=xx2−2x+1=xx−12．
3. 540
【解析】从某个多边形的一个顶点出发的对角线共有 2 条，则将多边形分割为 3 个三角形．
所以该多边形的内角和是 3×180∘=540∘．
4. 120
【解析】∵ 四边形 ABCD 内接于 ⊙O，∠BCD=120∘，
∴∠A=180∘−∠BCD=180∘−120∘=60∘，
故 ∠BOD=2∠A=2×60∘=120∘．
5. k>−1 且 k≠0
【解析】∵ 关于 x 的一元二次方程 kx2−2x−1=0 有两个不相等的实数根，
∴k≠0 且 Δ>0，即 −22−4×k×−1>0，解得 k>−1 且 k≠0．
∴k 的取值范围为 k>−1 且 k≠0．
6. 65 或 3
【解析】∵ 四边形 ABCD 为矩形，
∴∠BAD=90∘，
∴BD=AB2+AD2=10，
当 PD=DA=8 时，BP=BD−PD=2，
∵△PBE∽△DBC，
∴BPBD=PECD，即 210=PE6，
解得，PE=65，
当 PʹD=PʹA 时，点 Pʹ 为 BD 的中点，
∴PʹEʹ=12CD=3．
第二部分
7. B
8. C【解析】由题意得 1−x>0，解得 x<1．
9. A【解析】A、 2a2b−ba2=a2b，正确；
B、 a6÷a2=a4，故此选项错误；
C、 ab23=a2b6，故此选项错误；
D、 a+22=a2+4a+4，故此选项错误；
故选：A．
10. D
【解析】根据条形图可知：乘车的人数是 25 人，
∴ 总数是 25÷50%=50 人；
骑车人数在扇形图中占总人数的 20%；
则乘车人数是骑车人数的 2.5 倍；
步行人数为 30%×50=15 人．
11. C【解析】由正视图和左视图可确定此几何体为柱体，由俯视图是三角形可得此几何体为三棱柱．故选：C．
12. C【解析】∵AB∥x 轴，若点 B 的坐标为 1,3，
∴ 设点 Aa,3．
∵S△ABC=12a−1×3=2，
∴a=73．
∴ 点 A73,3．
∵ 点 A 在反比例函数 y=kxx>0 的图象上，
∴k=7．
13. A【解析】作 BM⊥ED 交 ED 的延长线于 M，
∵CF⊥DE，
在 Rt△CDF 中，
∵CFDF=43，CF=8，
∴DF=6，
∴CD=10，
∴CF=8，
∵ 四边形 BMNC 是矩形，
∴BM=CF=8，BC=MF=20，EM=MF+DF+DE=66，
在 Rt△AEM 中，tan24∘=AMEM，
∴0.45=8+AB66，
∴AB=21.7（米）．
14. B【解析】设 BC=a，则 AC=2a（a>0），
∴ 在 Rt△ACB 中，AB=AC2+BC2，
∴ a=25，BC=25，AC=45，
当 0≤x≤8 时，易证 △APQ∽△ACB，
∴ APAC=QPBC=x45，
∴ y=S△APQ=12AP×PQ=14x2，
当 8在 Rt△ABC 中，tanB=1tanA=2，
∴ PQ=BPtanB=210−x，
∴ y=S△APQ=12AP×PQ=12×x×2×10−x=10x−x2，
画出图象如答案B中图象所示．
第三部分
15. 原式=−2+1−4×32+23=−2+1−23+23=−1.
16. （1） M=1a−1a+1÷aa−1=1a−1a+1⋅a−1a=1a2+a.
（2） 1n−1n+1；nn+1
【解析】由题意可得 fn=1nn+1=1n−1n+1，
f1+f2+⋯+fn=1−12+12−13+13−14+⋯+1n−1n+1=1−1n+1=nn+1.
（3） 原不等式组化为
x−22−2−x4≤1−12+12−13+13−14, ⋯⋯①−x<1. ⋯⋯②
解不等式 ① 得：
x≤3.
解不等式 ② 得
x>−1.∴
不等式组的解集为：−1在数轴上表示如下：
17. 由作法可知 BF 是 ∠ABC 的角平分线，
∴∠ABF=∠CBF．
∵FG⊥AB，FH⊥BC，
∴∠FGB=∠FHB．
在 △GBF 和 △HBF 中，
∠FGB=∠FHB,∠GBF=∠HBF,BF=BF,
∴△GBF≌△HBFAAS，
∴BG=BH．
18. （1） 94；92；94
【解析】a=94；m=92，
n=11088+93+93+93+94+94+95+95+97+98=94．
（2） 八
【解析】七年级和八年级的平均数相同，但八年级的方差较小，所以八年级的成绩稳定．
（3） 列表得：
乙甲A1A2B1B2A1A1,A2A1,B1A1,B2A2A2,A1A2,B1A2,B2B1B1,A1B1,A2B1,B2B2B2,A1B2,A2B2,B1
共有 12 种等可能的结果，这两人分别来自不同年级的有 8 种情况，
∴P这两人分别来自不同年级的概率=812=23．
19. （1） 设该店 5 月份购进甲种水果 x 千克，购进乙种水果 y 千克．
根据题意得：
8x+18y=1700,10x+20y=1700+300.
解得：
x=100,y=50.
答：该店 5 月份购进甲种水果 100 千克，购进乙种水果 50 千克．
（2） 设购进甲种水果 a 千克，需要支付的货款为 w 元，则购进乙种水果 120−a 千克．
根据题意得：w=10a+20120−a=−10a+2400．
∵ 甲种水果不超过乙种水果的 3 倍，
∴a≤3120−a，解得：a≤90．
∵k=−10<0，
∴w 随 a 值的增大而减小，
∴ 当 a=90 时，w 取最小值，最小值 −10×90+2400=1500．
∴ 月份该店需要支付这两种水果的货款最少应是 1500 元．
20. （1） 连接 OB．
∵PA 为 ⊙O 相切于点 A，
∴∠OAP=90∘．
∵PO⊥AB，
∴AC=BC．
∴PA=PB．
在 △PAO 和 △PBO 中，
PA=PB,AO=BO,PO=PO,
∴△PAO≌△PBOSSS，
∴∠OBP=∠OAP=90∘，即 PB⊥OB．
∵OB 为 ⊙O 的半径，
∴PB 是 ⊙O 的切线．
（2） 在 Rt△ACO 中，OC=3，AC=4，
∴AO=5．
∵∠PAB+∠CAO=90∘，∠AOC+∠CAO=90∘，
∴∠PAB=∠AOC，
∴sin∠PAB=ACAO=45．
21. （1） 设 y 与 x 的函数关系式为 y=kx+b，
将 10,200，15,150 代入，
得：10k+b=200,15k+b=150, 解得：k=−10,b=300,
∴y 与 x 的函数关系式为 y=−10x+3008≤x≤30．
（2） 设每天销售获得的利润为 w，
则 w=x−8y=x−8−10x+300=−10x−192+1210，
∵8≤x≤30，
∴ 当 x=19 时，w 取得最大值，最大值为 1210．
（3） 由（2）知，当获得最大利润时，定价为 19 元/千克，
则每天的销售量为 y=−10×19+300=110 千克．
∵ 保质期为 40 天，
∴ 总销售量为 40×110=4400，
又 ∵4400<4800，
∴ 不能销售完这批蜜柚．
22. （1） 如图 1，连接 AC，
∵ 点 O，E，F，G 分别是 AB，BC，CD，AD 的中点，
∴OE∥AC，OE=12AC，GF∥AC，GF=12AC，
∴OE∥GF，OE=GF，
∴ 四边形 OEFG 是平行四边形．
（2） ① ∵△OGE 绕点 O 顺时针旋转得到 △OMN，
∴OG=OM，OE=ON，∠GOM=∠EON，
∴OGOE=OMON，
∴△OGM∽△OEN，
∴ENGM=OEOG=3．
②添加 AC=BD，如图 2，连接 AC，BD，
∵ 点 O，E，F，G 分别是 AB，BC，CD，AD 的中点，
∴OG=EF=12BD，OE=GF=12AC，
∵AC=BD，
∴OG=OE，
∵△OGE 绕点 O 顺时针旋转得到 △OMN，
∴OG=OM，OE=ON，∠GOM=∠EON，
∴OG=OE，OM=ON，
在 △OGM 和 △OEN 中，
∵OG=OE,∠GOM=∠EON,OM=ON,
∴△OGM≌△OENSAS，
∴GM=EN．
23. （1） 32,0；−1,0
【解析】∵ 对称轴 x=−−3a2a=32，
∴ 点 E 坐标 32,0．
令 y=0，则有 ax2−3ax−4a=0，
∴x=−1 或 4．
∴ 点 A 坐标 −1,0．
（2） 如图①中，设 ⊙E 与直线 BC 相切于点 D，连接 DE，则 DE⊥BC．
∵DE=OE=32，EB=52，OC=−4a，
∴DB=EB2−DE2=2.52−1.52=2，
∵tan∠OBC=DEBD=OCOB，
∴1.52=−4a4，
∴a=−34，
∴ 抛物线解析式为 y=−34x2+94x+3．
（3） 如图②中，由题意 ∠MʹCN=∠NCB，
∵MN∥OMʹ，
∴∠MʹCN=∠CNM，
∴MN=CM，
∵ 直线 BC 解析式为 y=−34x+3，
∴Mm,−34m+3，Nm,−34m2+94m+3，作 MF⊥OC 于 F，
∵sin∠BCO=FMMC=BOBC，
∴mCM=45，
∴CM=54m；
①当 N 在直线 BC 上方时，−34x2+94x+3−−34x+3=54m，
解得：m=73 或 0（舍弃），
∴Q173,0；
②当 N 在直线 BC 下方时，−34m+3−−34m2+94m+3=54m，
解得 m=173 或 0（舍弃），
∴Q2173,0．
综上所述：点 Q 坐标为 73,0 或 173,0．