2020-2021年安徽合肥市九年级上学期数学第一次月考试卷及答案

这是一份2020-2021年安徽合肥市九年级上学期数学第一次月考试卷及答案，共9页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。

 九年级上学期数学第一次月考试卷
一、单项选择题
1.以下函数是二次函数的是〔     〕
A. y=2x2-3                       B. y=ax2                       C. y=2〔x+3〕2-2x2                       D. 
2.函数y＝﹣x2﹣4x﹣3图象顶点坐标是(   )
A. (2，﹣1)                            B. (﹣2，1)                            C. (﹣2，﹣1)                            D. (2，1)
3.二次函数y=mx2+x+m〔m-2〕的图像经过原点，那么m的值为〔     〕
A. 0或2                                      B. 0                                      C. 2                                      D. 无法确定
4.函数 的图象经过的象限是〔    〕
A. 第一、二、三象限             B. 第一、二象限             C. 第三、四象限             D. 第一、二、四象限
5.如图，正方形ABOC的边长为2，反比例函数 的图象过点A，那么k的值是〔   〕

A. 2                                         B. ﹣2                                         C. 4                                         D. ﹣4
6.如图，正 的顶点A在反比例函数 (x＞0)的图象上，那么点B的坐标为〔    〕

A. (2，0)                           B. ( ，0)                           C. (2 ，0)                           D. ( ，0)
7.如图，抛物线y=ax2+bx+c〔a＞0〕的对称轴是直线x=1，且经过点P〔3，0〕，那么a-b+c的值为〔      〕

A. 0                                           B. -1                                           C. 1                                           D. 2
8.函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是〔   〕
A.           B.           C.           D. 
9.如图△OAP，△ABQ均是等腰直角三角形，点P，Q在函数y= 〔x＞0〕的图象上，直角顶点A，B均在x轴上，那么点B的坐标为〔　　〕

A. 〔 ，0〕                B. 〔 ，0〕                C. 〔3，0〕                D. 〔 ，0〕
10.如图 和 都是边长为2的等边三角形，它们的边 在同一条直线l上，点C，E重合，现将 沿着直线l向右移动，直至点B与F重合时停止移动．在此过程中，设点移动的距离为x，两个三角形重叠局部的面积为y，那么y随x变化的函数图像大致为〔   〕

A.                                   B. 
C.                                   D. 
二、填空题
11.抛物线 的顶点在y轴上，那么b的值为________．
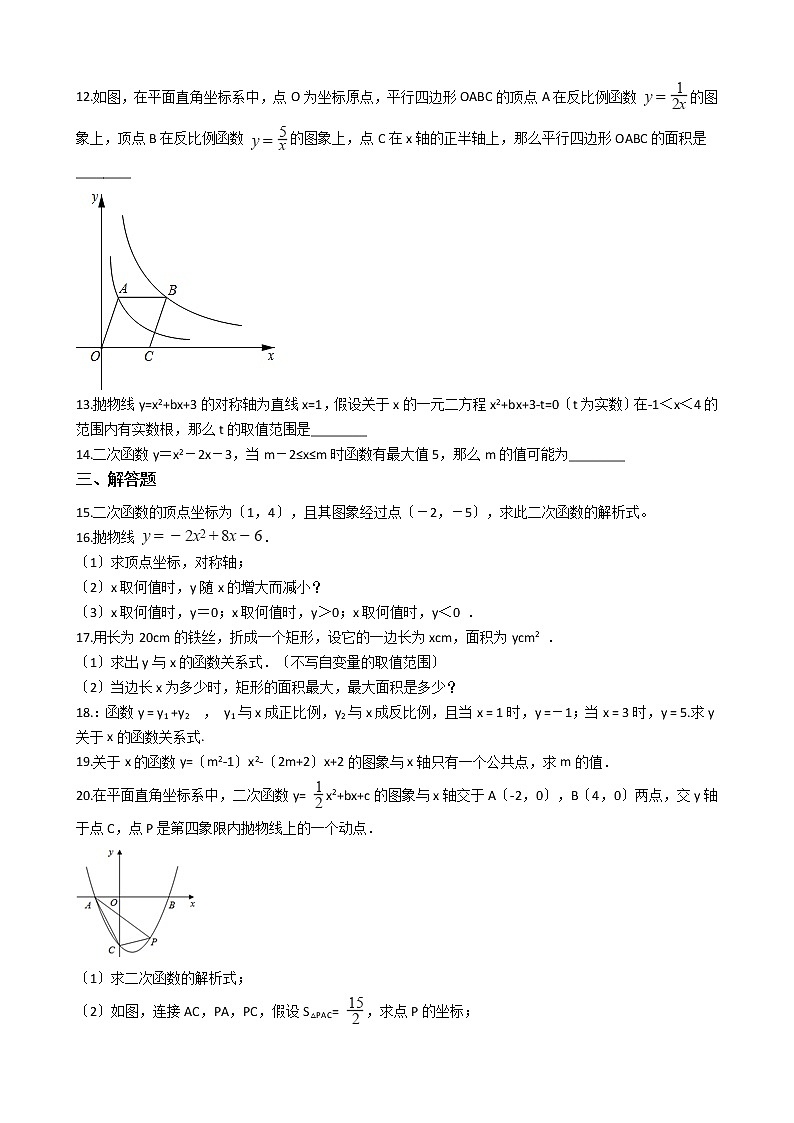
12.如图，在平面直角坐标系中，点O为坐标原点，平行四边形OABC的顶点A在反比例函数 的图象上，顶点B在反比例函数 的图象上，点C在x轴的正半轴上，那么平行四边形OABC的面积是________

13.抛物线y=x2+bx+3的对称轴为直线x=1，假设关于x的一元二方程x2+bx+3-t=0〔t为实数〕在-1＜x＜4的范围内有实数根，那么t的取值范围是________
14.二次函数y＝x2－2x－3，当m－2≤x≤m时函数有最大值5，那么m的值可能为________
三、解答题
15.二次函数的顶点坐标为〔1，4〕，且其图象经过点〔－2，－5〕，求此二次函数的解析式。
16.抛物线 ．
〔1〕求顶点坐标，对称轴；
〔2〕x取何值时，y随x的增大而减小？
〔3〕x取何值时，y＝0；x取何值时，y＞0；x取何值时，y＜0 ．
17.用长为20cm的铁丝，折成一个矩形，设它的一边长为xcm，面积为ycm2 ．
〔1〕求出y与x的函数关系式．〔不写自变量的取值范围〕
〔2〕当边长x为多少时，矩形的面积最大，最大面积是多少？
18.：函数y = y1 +y2 ， y1与x成正比例，y2与x成反比例，且当x = 1时，y =－1；当x = 3时，y = 5.求y关于x的函数关系式.
19.关于x的函数y=〔m2-1〕x2-〔2m+2〕x+2的图象与x轴只有一个公共点，求m的值．
20.在平面直角坐标系中，二次函数y= x2+bx+c的图象与x轴交于A〔-2，0〕，B〔4，0〕两点，交y轴于点C，点P是第四象限内抛物线上的一个动点．

〔1〕求二次函数的解析式；         
〔2〕如图，连接AC，PA，PC，假设S△PAC= ，求点P的坐标；
21.如图，A〔-4，n〕，B〔2，-4〕是一次函数y1=kx+b的图像和反比例函数 的图像的两个交点

〔1〕求反比例函数和一次函数的解析式
〔2〕求直线与x轴的交点C的坐标及△AOB的面积
〔3〕当x取何值时，y1=y2；当x取何值时，y1>y2
22.如图1，排球场长为18m ， 宽为9mm ． 队员站在底线O点处发球，球从点Om的C点发出，运动路线是抛物线的一局部，当球运动到最高点Am ． 即BAm ． 这时水平距离OB＝7m ， 以直线OB为x轴，直线OC为y轴，建立平面直角坐标系，如图2．

〔1〕假设球向正前方运动〔即x轴垂直于底线〕，求球运动的高度y〔m〕与水平距离x〔m〕之间的函数关系式〔不必写出x取值范围〕．并判断这次发球能否过网？是否出界？说明理由；
〔2〕假设球过网后的落点是对方场地①号位内的点P〔如图1，点P距底线1mm〕，问发球点O在底线上的哪个位置？〔参考数据： 〕
23.在平而直角坐标系中，点 ，直线 经过点A．抛物线 恰好经过 三点中的两点．
〔1〕判断点B是否在直线 上．并说明理由；
〔2〕求 的值；
〔3〕平移抛物线 ，使其顶点仍在直线 上，求平移后所得抛物线与 轴交点纵坐标的最大值．

答案解析局部
一、单项选择题
1.【解析】【解答】解：A. 是二次函数，故A.符合题意；
B. 中a是变量，故B.不符合题意；
C. 是一次函数，故C.不符合题意；
D. 中分母含有变量，故D.不符合题意．
故答案为：A．
【分析】一般地，形如 〔a，b，c是常数，且 〕的函数时二次函数，据此解题即可．
2.【解析】【解答】∵y=-x2-4x-3=-〔x2+4x+4-4+3〕=-〔x+2〕2+1
∴顶点坐标为〔-2，1〕；
故答案为：B.
【分析】将二次函数的一般式化为顶点式，从而求出结论.
3.【解析】【解答】解：∵二次函数y=mx2+x+m〔m-2〕的图象经过原点，
∴将〔0，0〕代入解析式，得：m〔m-2〕=0，
解得：m=0或m=2，
又∵二次函数的二次项系数m≠0，
∴m=2．
故答案为：C．
【分析】根据题意将〔0，0〕代入解析式，得出关于m的方程，解之得出m的值，由二次函数的定义进行分析可得答案．
4.【解析】【解答】解：∵ 的顶点坐标公式为( ， )
∴ 的顶点坐标为( ， )，
而 ，开口向上，
所以抛物线过第一，二象限．
故答案为：B．
【分析】利用公式法先求顶点坐标，再判断经过的象限．
5.【解析】【解答】解：因为图象在第二象限，
所以k＜0，
根据反比例函数系数k的几何意义可知|k|=2×2=4，
所以k=﹣4．
故答案为：D．
【分析】观察图像，可知双曲线分布在第二、四象限，根据正方形ABOC的边长为2，得出其面积为4，即可得k的值。
6.【解析】【解答】解：如图，过点A作 轴于C，

是正三角形，
，
，
设 ，那么 ，
点A那么坐标是 ，
把这点代入反比例函数的解析式就得到 ，
，
根据图象在第一象限， ，
那么 ，
，
那么点B的坐标为 ．
故答案为：A．
【分析】过点A作 轴于C，根据条件知道 是正三角形，然后设 AC=a ，那么 ，这样点A的坐标可以用a表示，再把这点代入反比例函数的解析式就可以求出a从而求出点B的坐标．
7.【解析】【解答】因为对称轴x=1且经过点P〔3，0〕
所以抛物线与x轴的另一个交点是〔-1，0〕
代入抛物线解析式y=ax2+bx+c中，得a-b+c=0．
故答案为：A．
【分析】根据抛物线的对称轴x=1及它经过点P〔3，0〕，可得出抛物线与x轴的另一个交点坐标为〔-1，0〕，将其代入函数解析式，可解答。
8.【解析】【解答】解：当a＞0时，二次函数的图象开口向上，
一次函数的图象经过一、三或一、二、三或一、三、四象限，
故A、D不正确；
由B、C中二次函数的图象可知，对称轴x=﹣ ＞0，且a＞0，那么b＜0，
但B中，一次函数a＞0，b＞0，排除B．
应选：C．
【分析】根据a、b的符号，针对二次函数、一次函数的图象位置，开口方向，分类讨论，逐一排除．
9.【解析】【解答】解：∵△OAP是等腰直角三角形，
∴PA=OA ，
∴设P点的坐标是〔a，a〕，
把〔a，a〕代入解析式得到a=2，
∴P的坐标是〔2，2〕，
那么OA=2，
∵△ABQ是等腰直角三角形，
∴BQ=AB，
∴设点Q的纵坐标是b，
∴点Q的横坐标是b+2，
把Q的坐标代入解析式y= ，
∴ ，
∴b= ﹣1，
∴b+2= ﹣1+2= +1，
∴点B的坐标为〔 +1，0〕，
故答案为：B．
【分析】由△OAP是等腰直角三角形可以得到PA=OA，可以设P点的坐标是〔a，a〕，把〔a，a〕代入反比例函数解析式即可求出a=2，然后求出P的坐标，从而求出OA，再根据△ABQ是等腰直角三角形用同样的方法即可求出点B的坐标．
10.【解析】【解答】C点移动到F点,重叠局部三角形的边长为x,由于是等边三角形,那么高为 ,面积为y=x· · = ,
B点移动到F点,重叠局部三角形的边长为(4－x),高为 ,面积为
y=(4－x)· · = ,
两个三角形重合时面积正好为 .
由二次函数图象的性质可判断答案为A,
故答案为：A.
【分析】根据图象可得出重叠局部三角形的边长为x,根据特殊角三角函数可得高为 ,由此得出面积y是x的二次函数,直到重合面积固定,再往右移动重叠局部的边长变为(4－x),同时可得
二、填空题
11.【解析】【解答】解：根据题意，把解析式转化为顶点形式为：
y=x2-〔b-2〕x+3b=〔x- 〕2+3b-〔 〕2 ，
顶点坐标为〔 ，3b-〔 〕2〕，
∵顶点在y轴上，
∴
∴b=2．
【分析】把抛物线解析式转化为顶点形式，即可得顶点坐标，再根据顶点在y轴上，即x=0，即可得b的值．
12.【解析】【解答】解：如图，作 轴于点D，延长BA交y轴于点E，

∵四边形OABC是平行四边形，
∴ ， ，
∴ 轴，
∴ ，
∴ ，
根据系数k的几何意义得， ， ， ，
∴四边形OABC的面积 ；
【分析】根据平行四边形的性质和反比例函数系数k的几何意义即可求解；
13.【解析】【解答】解：∵抛物线y=x2+bx+3的对称轴为直线x=1，
∴ =1，得b=-2，
∴y=x2-2x+3=〔x-1〕2+2，
∴当-1＜x＜4时，y的取值范围是2≤y＜11，
当y=t时，t=x2-2x+3，即x2+bx+3-t=0，
∵关于x的一元二次方程x2+bx+3-t=0〔t为实数〕在-1＜x＜4的范围内有实数根，
∴t的取值范围是2≤t＜11，
故答案为：2≤t＜11．
【分析】由题意根据抛物线y=x2+bx+3的对称轴为直线x=1，可以求得b的值，然后即可得到该函数的解析式，再根据二次函数的性质，即可得到当-1＜x＜4时，y的取值范围，然后令y=t，即可转化为方程x2+bx+3-t=0，从而可以得到t的取值范围．
14.【解析】【解答】解：y=x2-2x-3=〔x-1〕2-4，
∵抛物线的对称轴为直线x=1，
∴当m-2≤x≤m＜4时，x=-2时二次函数y=x2-2x-3的最大值为：y=4+4-3=5，符合题意，此时m=0；
当m≥4时，x=m时二次函数y=x2-2x-3的最大值为：m2-2m-3=5，
解得m1=4，m2=-2〔舍去〕．
综上所述，m的值为0或4都符合题意，6和-2都不符合题意．
故答案为：0或4
【分析】先求出抛物线的对称轴为直线x=-1，然后确定当x=4时取得最大值，代入函数解析式进行计算即可得解．
三、解答题
15.【解析】【分析】二次函数的顶点坐标为〔1，4〕，设抛物线的顶点式为y=a〔x-1〕2+4〔a≠0〕，将点〔-2，-5〕代入求a即可.
16.【解析】【分析】〔1〕根据配方法的步骤要求，将抛物线解析式的一般式转化为顶点式，可确定顶点坐标和对称轴；〔2〕由对称性x=-2，抛物线开口向下，结合图象，宽为确定函数的增减性；〔3〕判断函数值的符合，可以令y=0，解一元二次方程组x，再去根据抛物线的开口方向，确定函数值的符合与x的取值范围的对应关系.
17.【解析】【分析】〔1〕一边长为xcm，那么另一边长为〔20-2x〕，根据面积公式即可解答；〔2〕把函数解析式用配方法化简，得出y的最大值．
18.【解析】【分析】根据正比例函数和反比例函数的定义得到y1=kx，y2= ，那么y=kx+ ，再利用当x=1时，y= -1，当x=3时，y=5得到关于k、m的方程组，然后解方程组求出k、m，即可得到y与x之间的函数关系式；
19.【解析】【分析】需要分类讨论：该函数是一次函数和二次函数两种情况．
20.【解析】【分析】〔1〕根据题意，将点A、B坐标分别代入二次函数解析式中，即可解题；〔2〕〕连结OP，设 ，先求得点C的坐标，再根据 ，结合三角形面积公式解题即可．
21.【解析】【分析】〔1〕根据题意，点A、B在一次函数及反比例函数图象上，那么点A、B的坐标均符合两个解析式，将点B、A分别代入反比例函数求k、n的值，再将点A、B分别代入一次函数解析式中即可解题；〔2〕令直线 ，解得直线与x轴的交点坐标C，根据 及三角形面积公式解题即可；〔3〕观察图象，图象的公共点即为解析式的公共解，两个交点将图象分成四个区域，找到 的区域，写出其x的取值范围即可．
22.【解析】【分析】〔1〕求出抛物线表达式，再确定x＝9和x＝18时，对应函数的值即可求解；〔2〕当y＝0时，y＝﹣ 〔x﹣7〕2+2.88＝0，解得：x＝19或﹣5〔舍去﹣5〕，求出PQ＝6 ＝8.4，即可求解．
23.【解析】【分析】〔1〕先将A代入 ，求出直线解析式，然后将将B代入看式子能否成立即可；〔2〕先跟抛物线 与直线AB都经过〔0，1〕点，且B，C两点的横坐标相同，判断出抛物线只能经过A，C两点，然后将A，C两点坐标代入 得出关于a，b的二元一次方程组；〔3〕设平移后所得抛物线的对应表达式为y=-〔x-h〕2+k，根据顶点在直线 上，得出k=h+1，令x=0，得到平移后抛物线与y轴交点的纵坐标为-h2+h+1，在将式子配方即可求出最大值．