2019-2020学年山东青岛崂山区九上期末数学试卷
展开一、选择题(共8小题;共40分)
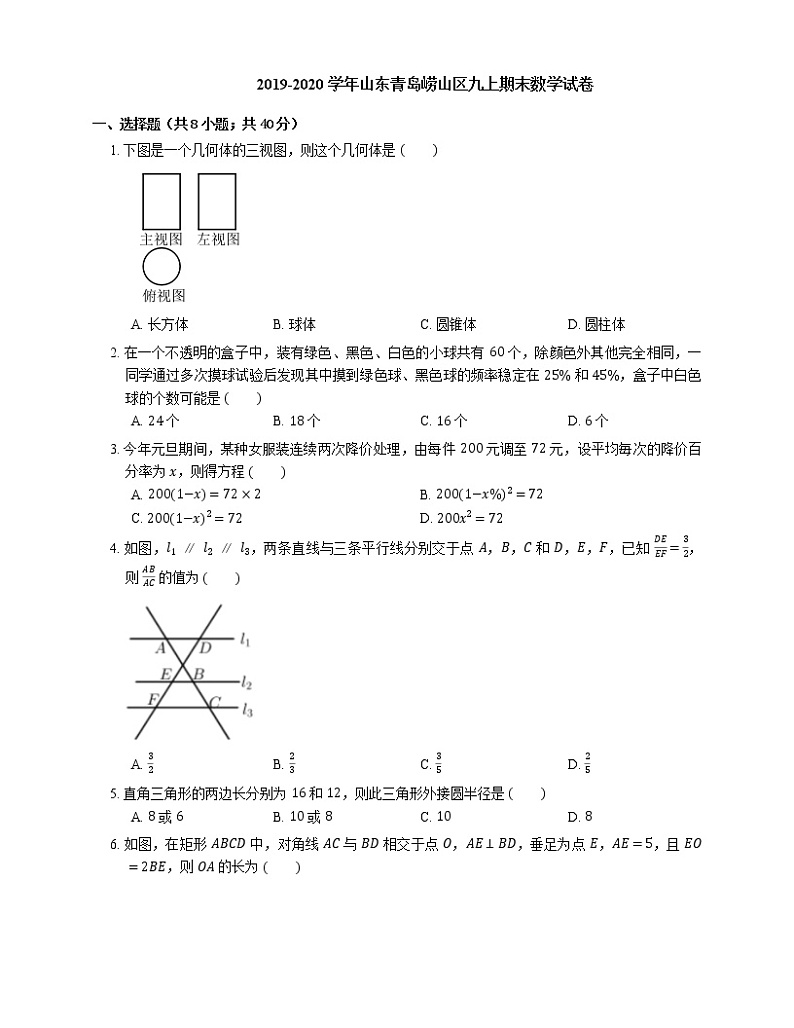
1. 下图是一个几何体的三视图,则这个几何体是
A. 长方体B. 球体C. 圆锥体D. 圆柱体
2. 在一个不透明的盒子中,装有绿色、黑色、白色的小球共有 60 个,除颜色外其他完全相同,一同学通过多次摸球试验后发现其中摸到绿色球、黑色球的频率稳定在 25% 和 45%,盒子中白色球的个数可能是
A. 24 个B. 18 个C. 16 个D. 6 个
3. 今年元旦期间,某种女服装连续两次降价处理,由每件 200 元调至 72 元,设平均毎次的降价百分率为 x,则得方程
A. 2001−x=72×2B. 2001−x%2=72
C. 2001−x2=72D. 200x2=72
4. 如图,l1∥l2∥l3,两条直线与三条平行线分别交于点 A,B,C 和 D,E,F,已知 DEEF=32,则 ABAC 的值为
A. 32B. 23C. 35D. 25
5. 直角三角形的两边长分别为 16 和 12,则此三角形外接圆半径是
A. 8 或 6B. 10 或 8C. 10D. 8
6. 如图,在矩形 ABCD 中,对角线 AC 与 BD 相交于点 O,AE⊥BD,垂足为点 E,AE=5,且 EO=2BE,则 OA 的长为
A. 5B. 25C. 35D. 151313
7. 如图,在平面直角坐标中,正方形 ABCD 与正方形 BEFG 是以原点 O 为位似中心的位似图形,且相似比为 13,点 A,B,E 在 x 轴上,若正方形 BEFG 的边长为 12,则 C 点坐标为
A. 6,4B. 6,2C. 4,4D. 8,4
8. 已知反比例函数 y=abx 的图象如图所示,则二次函数 y=ax2−2x 和一次函数 y=bx+a 在同一平面直角坐标系中的图象可能是
A. B.
C. D.
二、填空题(共6小题;共30分)
9. 计算 sin260∘+cs60∘⋅2−1 .
10. 小莉身高 1.50 m,在阳光下的影子长为 1.20 m,在同一时刻站在阳光下,小林的影子长比小莉长 0.2 m,则小林的身高为 m.
11. 如图,A,B,C,D 是 ⊙O 上四个点,连接 OA,OC,过 A 作 AE⊥OC 交圆周于点、 E,连接 OE,若 ∠ABC=140∘,则 ∠OEA 的度数为 .
12. 如图,在平行四边形 ABCD 中,E 是 AB 边上的点,AE=3BE,连接 AC,DE 相交于 O,则 S△AOE:S△ACD= .
13. 如图,已知反比例函数 y=kxk>0 的图象经过 Rt△OAB 斜边 OB 的中点 D,与直角边 AB 相交于点 C,若 △OBC 的面积为 8,则 k 的值为 .
14. 如图,在 Rt△ABC 中,∠ABC=90∘,BD 为 AC 边上的中线,过点 C 作 CE⊥BD 于点 E,过点 A 作 BD 的平行线,交 CE 的延长线于点 F,在 AF 的延长线上截取 FG=BD,连接 BG,DF.若 AG=26,BG=10,则 CF 的长为 .
三、解答题(共10小题;共130分)
15. 已知:△ABC.
求作:菱形 DBEC,使菱形的顶点 D 落在 AC 边上.
结论:
16. 解方程.
(1)解方程:x2−5x+1=0(配方法).
(2)已知二次函数:y=mx2−12x+18 与 x 轴只有一个交点,求此交点坐标.
17. 在学习“轴对称现象”内容时,老师让同学们寻找身边的轴对称图形.小明利用手中的一副三角尺和一个量角器(如图所示)进行探究.
(1)小明在这三件文具中任取一件,结果是轴对称图形的概率是 (取三件中任意一件的可能性相同).
(2)小明发现在 A,B 两把三角尺中各选一个角拼在一起(无重叠无缝隙)会得到一个更大的角,若每个角选取的可能性相同、请用画树状图或列表的方法说明拼成的角是钝角的概率是多少.
18. 一位橄榄球选手掷球时,橄榄球从出手开始行进的高度 ym 与水平距离 xm 之间的关系如图所示,已知橄榄球在距离原点 6 m 时,达到最大高度 7 m,橄榄球在距离原点 13 米处落地,请根据所给条件解决下面问题:
(1)求出 y 与 x 之间函数关系式.
(2)求运动员出手时橄榄球的高度.
19. 如图,山顶有一塔 AB.塔高 33 m,计划在塔的正下方沿直线 CD 开通穿山隧道 EF.从与 E 点相距 80 m 的 C 处测得 A,B 的仰角分别为 27∘,22∘,从与 F 点相距 50 m 的 D 处测得 A 的仰角为 45∘.求隧道 EF 的长度.(参考数据:tan22∘≈0.40,tan27∘≈0.51.)
20. 阅读材料:以下是我们教科书中的一段内容,请仔细阅读,并解答有关问题.
公元前 3 世纪,古希腊学家阿基米德发现:若杠杆上的两物体与支点的距离与其重量成反比,则杠杆平衡,后来人们把它归纳为“杠杆原理”,通俗地说,杠杆原理为:阻力 × 阻力臂 = 动力 × 动力臂.
(1)【问题解决】
若工人师傅欲用撬棍动一块大石头,已知阻力和阻力臂不变,分别为 1500 N 和 0.4 m.
(1)动力 FN 与动力臂 lm 有怎样的函数关系?当动力臂为 1.5 m 时,撬动石头需要多大的力?
(2)若想使动力 FN 不超过题(1)中所用力的一半,则动力臂至少要加长多少?
(2)【数学思考】
请用数学知识解释:我们使用撬棍,当阻力与阻力臂一定时,为什么动力臂越长越省力.
21. 如图,四边形 ABCD 是平行四边形,连接对角线 AC,过点 D 作 DE∥AC 与 BC 的延长线交于点 E,连接 AE 交 DC 于 F.
(1)求证:BC=CE.
(2)连接 BF,若 ∠DAF=∠FBE,且 AD=2CF,求证:四边形 ABCD 是正方形.
22. 社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为 52 米,宽为 28 米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为 640 平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位 64 个,据调查分析,当每个车位的月租金为 200 元时,可全部租出;当每个车位的月租金每上涨 10 元,就会少租出 1 个车位,当每个车位的月租金上涨多少元时,停车场的月租金收入为 14400 元?
23. 问题提出:
如图所示,有三根针和套在一根针上的若干金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
1.每次只能移动 1 个金属片;
2.较大的金属片不能放在较小的金属片上面.
把 n 个金属片从 1 号针移到 3 号针,最少移动多少次?
问题探究:为了探究规律,我们采用一般问题特殊化的方法,先从简单的情形入手,再逐次递进,最后得出一般性结论.
探究一:当 n=1 时,只需把金属片从 1 号针移到 3 号针,用符号 1,3 表示,共移动了 1 次.
探究二:当 n=2 时,为了避免将较大的金属片放在较小的金属片上面,我们利用 2 号针作为“中间针”,移动的顺序是:
1.把第 1 个金属片从 1 号针移到 2 号针:
2.把第 2 个金属片从 1 号针移到 3 号针;
3.把第 1 个金属片从 2 号针移到 3 号针,
用符号表示为:1,21,32,3 共移动了 3 次.
探究三:当 n=3 时,把上面两个金属片作为一个整体,则归结为 n=2 的情形,移动的顺序是:
1.把上面两个金属片从 1 号针移到 2 号针;
2.把第 3 个金属片从 1 号针移到 3 号针;
3.把上面两个金属片从 2 号针移到 3 号针.,
其中(1)和(3)都需要借助中间针,用符号表示为:1,31,23,2;1,3;2,12,31,3 共移动了 7 次.
(1)探究四:请仿照前面步骤进行解答:
当 n=4 时,把上面 3 个金属片作为一个整体,移动的顺序是: .
(2)探究五:根据上面的规律你可以发现当 n=5 时,需要移动 .
(3)探究六:把 n 个金属片从 1 号针移到 3 号针,最少移动 次.
(4)探究七:如果我们把 n 个金属片从 1 号针移到 3 号针,最少移动的次数记为 an,当 n≥2 时如果我们把 n−1 个金属片从 1 号针移到 3 号针,最少移动的次数记为 an−1,那么 an 与 an−1 的关系是 an= .
24. 已知,如图 1,在平行四边形 ABCD 中,对角线 AC=6 cm,BC=8 cm,AB=10 cm,如图 2,点 G 从点 B 出发,沿 BC 方向匀速运动,速度为 1 cm/s,过点 G 作 GH⊥BC 交 AB 于点 H;将平行四边形 ABCD 沿对角线 AC 剪开,△DEF 从图 1 的位置与点 G 同时出发,沿射线 BC 方向匀速运动,速度为 2 cm/s,当点 G 停止运动时,△DEF 也停止运动.设运动时间为 t0
(2)设四边形 AHGD 的面积为 Scm2,试确定 S 与 t 的函数关系式.
(3)当 t 为何值时,S 有最大值?
(4)连接 EG,试求当 AG 平分 ∠BAC 时,四边形 EGFD 与四边形 AHGE 面积之比.
答案
第一部分
1. D【解析】主视图为长方形,左视图为长方形,俯视图为圆,
∴ 这个几何体为圆柱.
2. B【解析】绿球:60×25%=15(个).
黑球:60×45%=27(个).
∴ 白球:60−15−27=18(个).
∴ 故选B.
3. C【解析】每次降价百分率为 x,
则第一次为 2001−x,
第二次为 2001−x2,
∴2001−x2=72.
故选:C.
4. C【解析】由平行线分线段成比例定理可得:
DEEF=ABBC=32,
∴ABAC=ABAB+BC=33+2=35,
故答案选C.
5. B
【解析】应分为两种情况讨论:
①当 16 为斜边时,此时外接圆直径为 8;
②当 16 和 12 为直角三角形直角边时,
根据勾股定理可知:162+122=202,
此时斜边长为 20,
故外接圆半径为 10.
故选B.
6. C【解析】由题意得:四边形 ABCD 为矩形,
∴OA=OB,
设 BE=x,则 EO=2BE=2x,
∴OB=OA=BE+OE=3x,
在 Rt△AEO 中,AE2+OE2=OA2,
∴25+4x2=9x2,
解得 x1=5,x2=−5(舍),
∴OA=3x=35.
故选C.
7. A【解析】∵ 正方形 ABCD 与正方形 BEFG 是以原点 O 为位似中心的位似图形,且相似比为 1:3,
∴AD:BG=1:3,
∵BG=12,
∴AD=BC=4,
∵AD∥BG ,
∴△OAD∽△OBG,
∴OA:OB=1:3,
解得:OA=2,
∴OB=6,
∴C 点坐标为:6,4.
故选:A.
8. C【解析】∵ 当 x=0 时, y=ax2−2x=0 ,即抛物线 y=ax2−2x 经过原点,故A错误;
∵ 反比例函数 y=abx 的图象在第一、三象限,
∴ab>0 ,即 a , b 同号,
当 a<0 时,抛物线 y=ax2−2x 的对称轴 x=1a<0 ,对称轴在 y 轴左边,故D错误;
当 a>0 时, b>0 ,直线 y=bx+a 经过第一、二、三象限,故B错误,C正确.
故选:C.
第二部分
9. 1
【解析】sin260∘+cs60∘⋅2−1=322+12×12=34+14=1.
10. 1.75
【解析】设小林身高为 x,
则 +0.2,
∴x=1.75.
故答案为:1.75.
11. 10∘
【解析】∵A,B,C,D 是 ⊙O 上四个点,
∴ 四边形 ABCD 为 ⊙O 的内接四边形,
∴∠ABC+∠D=180∘,
∵∠ABC=140∘,
∴∠D=180∘−140∘=40∘,
∴∠AOC=2∠D=80∘,
∵AE⊥OC,
∴AC=CE,
∴∠AOC=∠COE=80∘,
∴∠AOE=∠AOC+∠COE=160∘,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠OEA=12180∘−∠AOE=12×180∘−160∘=10∘.
12. 9:28
【解析】∵ 四边形 ABCD 为平行四边形,
∴AB=CD,AE∥CD,
∴△AOE∽△COD,
∴AOOC=AECD.
∵AE=3BE,
∴AECD=34,
∴AOOC=34.
且 S△AOES△COD=AECD2=916,
∵△AOD 和 △COD 以 AO,CO 为底时,高是相同的.
∴S△AODS△DOC=AOOC=34,
设 S△AOB=9S,
则 S△COD=16S,S△AOD=12S,
S△ACD=S△AOD+S△COD=28S.
∴S△AOB:S△ACD=9S:28S=9:28.
13. 163
【解析】过 D 点作 x 轴的垂线交 x 轴于 E 点,
∵△ODE 的面积和 △OAC 的面积相等,
∴△OBC 的面积和四边形 DEAB 的面积相等且为 4.
设 D 点的横坐标为 x,纵坐标就为 kx,
∵D 为 OB 的中点,
∴EA=x,AB=2kx.
∴ 面积 DEAB 为:12kx+2kx⋅x=8,
∴k=163.
故答案为:163.
14. 12
【解析】∵AG∥BD,BD=FG,
∴ 四边形 BGFD 是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又 ∵ 点 D 是 AC 中点,
∴BD=DF=12AC,
∴ 四边形 BGFD 是菱形,
∴GF=BG=10,则 AF=26−10=16,AC=2×10=20,
∵ 在 Rt△ACF 中,∠CFA=90∘,
∴AF2+CF2=AC2,即 162+CF2=202,得:CF=12.
第三部分
15. 作图步骤如下:
分别以 B,C 为圆心,任意长度为半径画圆,
取两圆相交时的交点 M,N,
连接 M,N 交 BC 于 O 点,交 AC 于 D 点,
以 O 为圆心,OD 长度为半径画圆交 MN 于 E 点,
连接 BE,CE,
则四边形 DBEC 为菱形,如图.
16. (1)
x2−5x+1=0.x2−5x+522=−1+522.x−522=254−44=214.∴x−52=±212.∴x1=212+52=5+212.x2=−212+52=5−212.∴
原方程解为:
x1=5+212,x2=5−212.
(2) 与 x 轴只有 1 个交点,
∴Δ=b2−4ac=−122−4m×18=144−72m=0,
∴m=2,
∴y=2x2−12x+18=2x2−6x+9=2x−32,
∴y=0 时,2x−32=0,
∴x−3=0,
∴x=3.
∴ 交点为 3,0.
17. (1) 23
(2) 设角为 90∘,60∘,45∘,30∘ 分别为 A1,A2,B,C1,C2,D,
画树状图如图所示:
一共有 18 种结果,每种结果出现的可能性是相同的,
而其中可以拼成的这个角是钝角的结果有 12 种,
∴ 这个角是钝角的概率是 1218=23.
18. (1) 设橄榄球运动高度和水平距离满足的解析式为:y=ax−h2+k.
由题意可得:函数顶点坐标为 6,7,与 x 轴交点坐标为 13,0.
将 13,0 代入 y=ax−62+7 中得:49a+7=0,解得 a=−17.
∴ 解析式为 y=−17x−62+7.
(2) 令 x=0,y=−17×36+7=137.
答:运动员出手时高度为 137 m.
19. 如图,延长 AB 交 CD 于点 H,则 AH⊥CD.
在 Rt△ACH 中,∠ACH=27∘,
∵tan27∘=AHCH,
∴AH=CH⋅tan27∘.
在 Rt△BCH 中,∠BCH=22∘,
∵tan22∘=BHCH,
∴BH=CH⋅tan22∘,
∵AB=AH−BH,
∴CH⋅tan27∘−CH⋅tan22∘=33.
∴CH≈300.
∴AH=CH⋅tan27∘≈153.
在 Rt△ADH 中,∠D=45∘,
∵tan45∘=AHHD,
∴HD=AH=153.
∴EF=CD−CE−FD=CH+HD−CE−FD=300+153−80−50=323.
因此,隧道 EF 的长度约为 323 m.
20. (1) (1)根据“杠杆定律”有 FL=1500×0.4,
∴ 函数的解析式为 F=600L,
当 L=1.5 时,F=6001.5=400,
因此,撬动石头需要 400 N 的力.
(2)由(1)知 FL=600,
∴ 函数解析式可以表示为:l=600F,
当 F=400×12=200 时,l=600200=3,3−1.5=1.5m,
因此若用力不超过 400 N 的一半,则动力臂至少要加长 1.5 米.
(2) ∵ 撬棍工作原理遵循“杠杆定律”,当阻力与阻力臂一定时,其乘积为常数,
设其为 k,则动力 F 与动力臂 L 的函数关系式为 F=kL,
根据反比例函数的性质可知,动力 F 随动力臂 l 的增大而减小,
∴ 动力臂越长越省力.
21. (1) ∵ 四边形 ABCD 是平行四边形,
∴AD=BC,AD∥BC,
∵DE∥AC,
∴ 四边形 ACED 是平行四边形,
∴AD=CE,
∴BC=CE.
(2) ∵ 四边形 ACED 是平行四边形,
∴AD∥CE,DF=FC=12DC,
∴∠DAF=∠FEB,
∵∠DAF=∠FBE,
∴∠FEB=∠FBE,
∴FB=FE,
∵BC=CE,
∴∠FCB=90∘,
∴ 平行四边形 ABCD 为矩形,
∵AD=2CF,CF=12DC,
∴AD=DC,
∴ 矩形 ABCD 为正方形.
即四边形 ABCD 为正方形.
22. (1) 如图.
设通道宽是 x m,则铺起砖部分矩形长 52−2xm,宽 28−2xm,
故
S=52−2x28−2x=640.
解得
x=34舍,x=6 m.
故通道宽 6 m.
(2) 设每个车位月租金上涨 m 元,
则单位月租金为 200+m 元,可租出 64−m10 个车位,
则
200+m64−m10=14400.
解得
m=400 或 40.
即当每个车位的月租金上涨 400 元或 40 元时,总租金为 14400 元.
23. (1) 1,3,1,2,3,2,1,3,2,1,2,3,1,3,1,2,3,2,3,1,2,1,3,2,1,3,1,2,3,2
【解析】n=4 时,把上面 3 个金属片作为一个整体:
1.把上面三个金属片从 1 号针移到 2 号针;
2.把第 4 个金属片从 1 号针移到 3 号针;
3.把上面三个金属片从 2 号针移到 3 号针其中 1 和 3 都需借助中间针;
当把上面三个金属片从 1 号移到 2 号需把前面两个金属片移到 3 号 1,3,
另一个金属片移到 2 号 1,2,再将两个金属移到 2 号 3,2,
而把前面 2 个金属片移到 3 号,
需 1 个移到 2 号 1,2,1 个移到 3 号 1,3,再将 2 号移到 3 号 2,3,
当把上面三个金属片从 2 号针移到 3 号针需把前面 2 个金属片移到 1 号 2,1,
另一个移到 3 号 2,3,再将 2 个移到 3 号 1,3,
而把前 2 个移到 1 号,一个移 1 号 2,1,一个移 3 号 2,3,再将 3 号移 1 号 3,1,
∴ 移动顺序为:1,3,1,2,3,2,1,3,2,1,2,3,1,3,1,2,3,2,3,1,2,1,3,2,1,3,1,2,3,2.
(2) 31
【解析】∵n=1 时,移动 1 次,
n=2 时,移动 3 次 =22−1,
n=3 时,移动 7 次 =23−1,
n=4 时,移动 15 次 24−1,
n=5 时,移动 25−1=31.
(3) 2n−1
(4) 2n−1
【解析】an=2n−1,an−1=2n−1−1,
∴an−an−1=2n−2n−1=2n−1.
24. (1) ∵ 点 F 在线段 GD 的垂直平分线上,
∴FG=FD.
∵ 四边形 ABCD 是平行四边形,
∴AB=DF=10,
∴FG=10.
∵BG=t,AE=CF=2t,
∴BF=BC+CF=8+2t
=BG+FG=10+t,
∴8+2t=10+t,
∴t=1.
(2) 连接 AG.
S四边形AHGD=S△AHG+S△ADG=12HG⋅CG+12AD⋅AC.
∵tan∠B=HGBG=ACBC=68=34,
∴HG=34t,CG=BC−BG=8−t,AD=AE+DE=2t+8,
∴S四边形AHGD=S△AHG+S△ADG=12×34t×8−t+12×2t+8×6=3t−38t2+6t+24=−38t2+9t+24.
∴S=−38t2+9t+240
∴ 当 0
(4) ∵AG 平分 ∠BAC,
∴S△ABGS△ACG=ABAC=BGCG=106=53,
∴BG=58BC=58×8=5,CG=3,
∴AE=CF=10,FG=CG+CF=13,
∴HG=34BG=154,
∴S四边形EGFD=12DE+FG×EF=12×8+13×6=63,
S四边形AHGE=S△AHG+S△AEG=12HG×CG+12×AE×AC=12×154×3+12×10×6=458+30=2858,
∴S四边形EGFDS四边形AHGE=504285,
∴ 四边形 EGFD 与四边形 AHGE 面积之比为 504:285.
2018-2019学年山东省青岛市崂山区九上期末数学试卷: 这是一份2018-2019学年山东省青岛市崂山区九上期末数学试卷,共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2018-2019学年山东省青岛市崂山区七上期末数学试卷: 这是一份2018-2019学年山东省青岛市崂山区七上期末数学试卷,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2019-2020学年山东青岛黄岛区九上期末数学试卷: 这是一份2019-2020学年山东青岛黄岛区九上期末数学试卷,共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












