2019-2020学年山东省青岛市即墨区第二十八中学九上期末数学试卷

这是一份2019-2020学年山东省青岛市即墨区第二十八中学九上期末数学试卷，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 一元二次方程 x2=2x 的根是
A. x=2B. x=0C. x1=0，x2=2D. x1=0，x2=−2

2. 已知 ab=23，那么 aa+b 的值为
A. 13B. 25C. 35D. 34

3. 一元二次方程 x2−8x+1=0 配方后可变形为
A. x−42=15B. x+42=15C. x−42=17D. x+42=17

4. 在四边形 ABCD 中，对角线 AC，BD 相交于点 O，AO=CO，BO=DO，添加下列条件，不能判定四边形 ABCD 是菱形的是
A. AB=ADB. AC=BD
C. AC⊥BDD. ∠ABO=∠CBO

5. 用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色．那么可配成紫色的概率是
A. 14B. 34C. 13D. 12

6. 一个不透明的口袋里装有除颜色外都相同的 5 个白球和若干个红球，在不允许将球倒出来数的前提下，小亮为了估计其中的红球数，采用如下方法：现将口袋中的球摇匀，再从口袋里随机摸出一球，记下颜色，然后把它放回口袋中，不断重复上述过程，小亮共摸了 100 次，其中有 10 次摸到白球．因此小亮估计口袋中的红球大约有 个．
A. 45B. 48C. 50D. 55

7. 如图，在矩形 ABCD 中，AB=4，BC=6，点 E 为 BC 的中点，将 △ABE 沿 AE 折叠，使点 B 落在矩形内点 F 处，连接 CF，则 CF 的长为
A. 95B. 185C. 165D. 125

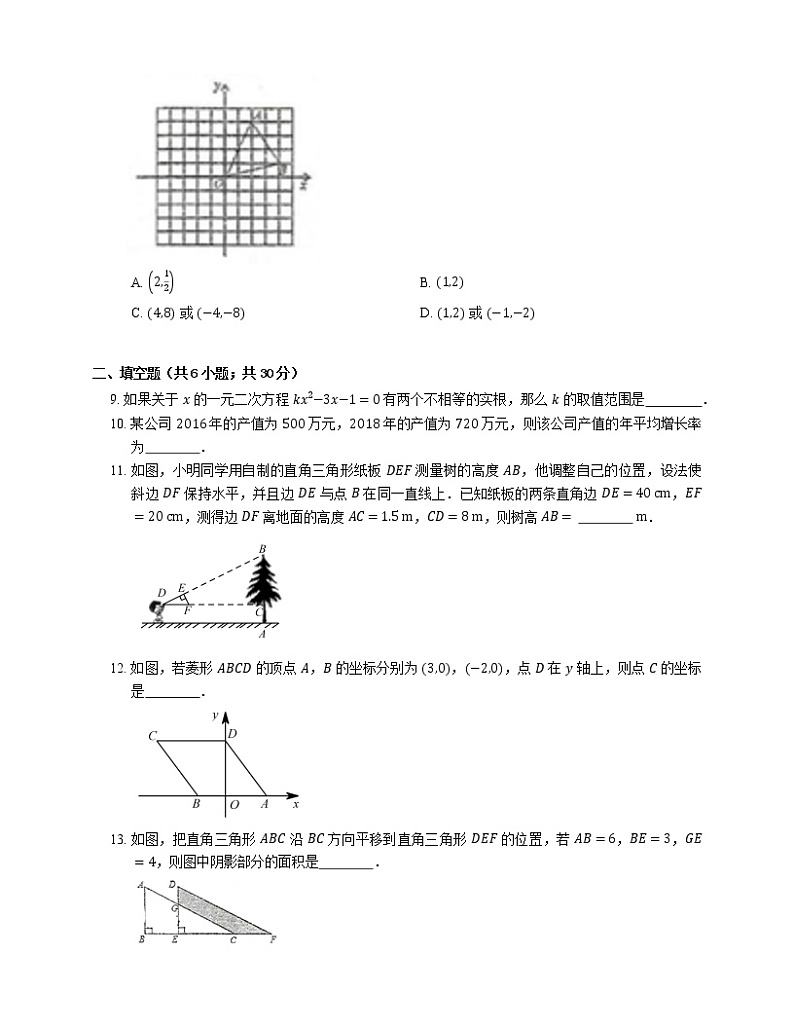
8. 如图，在平面直角坐标系中，已知点 A2,4，B4,1，以原点 O 为位似中心，将 △OAB 缩小为原来的 12，则点 A 的对应点 Aʹ 的坐标是
A. 2,12B. 1,2
C. 4,8 或 −4,−8D. 1,2 或 −1,−2

二、填空题（共6小题；共30分）
9. 如果关于 x 的一元二次方程 kx2−3x−1=0 有两个不相等的实根，那么 k 的取值范围是 ．

10. 某公司 2016 年的产值为 500 万元，2018 年的产值为 720 万元，则该公司产值的年平均增长率为 ．

11. 如图，小明同学用自制的直角三角形纸板 DEF 测量树的高度 AB，他调整自己的位置，设法使斜边 DF 保持水平，并且边 DE 与点 B 在同一直线上．已知纸板的两条直角边 DE=40 cm，EF=20 cm，测得边 DF 离地面的高度 AC=1.5 m，CD=8 m，则树高 AB= m．

12. 如图，若菱形 ABCD 的顶点 A，B 的坐标分别为 3,0，−2,0，点 D 在 y 轴上，则点 C 的坐标是 ．

13. 如图，把直角三角形 ABC 沿 BC 方向平移到直角三角形 DEF 的位置，若 AB=6，BE=3，GE=4，则图中阴影部分的面积是 ．

14. 如图，下列几何体是由棱长为 1 的小立方体按一定规律在地面上摆成的，若将露出的表面都涂上颜色（底面不涂色），则第 n 个几何体中只有两个面涂色的小立方体共有 个．

三、解答题（共10小题；共130分）
15. 一块直角三角形的木板余料，要在上面裁出一块正方形木板，要求：正方形的一个顶点在 C 点，有两条边在木板的直角边上，且面积最大．

16. 解方程．
（1）3x2+x−5=0（公式法）．
（2）x−32+2xx−3=0．

17. 小颖和小丽做“摸球”游戏：在一个不透明的袋子中装有编号为 1∼4 的四个球（除编号外都相同），从中随机摸出一个球，记下数字后放回，再从中摸出一个球，记下数字，若两次数字之和大于 5，则小颖胜，若两次数字之和小于 5，小丽胜，这个游戏对双方公平吗?请说明理由．

18. 已知 2+3 是方程 x2−4x+c=0 的一个根，求方程的另一个根及 c 的值．

19. 如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园 ABCD（围墙 MN 最长可利用 25 m），现在已备足可以砌 50 m 长的墙的材料，试设计一种砌法，使矩形花园的面积为 300 m2．

20. 有一块三角形的余料 ABC，∠BAC 为 90∘，一条直角边 AC 为 1.5 米，另一条直角边 AB 为 2 米，要把它加工成一个矩形，使矩形的一边 EF 落在 BC 上，其余两个顶点 D，G 分别在 AB，AC 上，且 DG=2DE，求矩形 DEFG 的长和宽分别是多少?

21. 如图，平行四边形 ABCD 中，过 A 作 AM⊥BC 于 M，交 BD 于 E，过 C 作 CN⊥AD 于 N，交 BD 于 F，连接 AF，CE．
（1）求证：△ABE≌△CDF．
（2）当四边形 ABCD 满足什么条件时，四边形 AECF 是菱形?证明你的结论．

22. 某校九年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作，已知该水果的进价为 8 元/千克，下面是他们在活动结束后的对话．
小丽：如果以 10 元/千克的价格销售，那么每天可售出 100 千克．
小强：如果以 12 元/千克的价格销售，那么每天可售出 80 千克．
小红：通过调查验证，我发现每天的销售量 y（千克）与销售单价 x（元）之间存在一次函数关系.
小强：我发现每天的销售量在 70 千克至 100 千克之间．
那么当销售单价为何值时，该超市销售这种水果每天获取的利润为 320 元?

23. 阅读理解．
如图 1，△ABC 中，沿 ∠BAC 的平分线 AB1 折叠，剪掉重叠部分；将余下部分沿 ∠B1A1C 的平分线 A1B2 折叠，剪掉重叠部分；⋯⋯；将余下部分沿 ∠BnAnC 的平分线 AnBn+1 折叠，点 Bn 与点 C 重合，无论折叠多少次，只要最后一次恰好重合，我们就称 ∠BAC 是 △ABC 的好角．
情形一：如图 2，沿等腰三角形 ABC 顶角 ∠BAC 的平分线 AB1 折叠，点 B 与点 C 重合；
情形二：如图 3，沿 △ABC 的 ∠BAC 的平分线 AB1 折叠，剪掉重叠部分；将余下的部分沿 ∠B1A1C 的平分线 A1B2 折叠，此时点 B1 与点 C 重合．
（1）探究发现．
△ABC 中，∠B=2∠C，经过两次折叠，问 ∠BAC △ABC 的好角（填写“是”或“不是”）；
（2）若经过三次折叠发现 ∠BAC 是 △ABC 的好角，请探究 ∠B 与 ∠C（假设 ∠B>∠C）之间的等量关系 ；
根据以上内容猜想：若经过 n 次折叠 ∠BAC 是 △ABC 的好角，则 ∠B 与 ∠C（假设 ∠B>∠C）之间的等量关系为 ．
（3）应用提升．
小丽找到一个三角形，三个角分别为 15∘，60∘，105∘，发现 是此三角形的好角；
（4）如果一个三角形的最小角是 10∘，且满足该三角形的三个角均是此三角形的好角，则此三角形另外两个角的度数 ．

24. 如图，在矩形 ABCD 中，AB=6 cm，AD=8 cm，点 P 从点 A 出发沿 AD 向点 D 匀速运动，速度是 1 cm/s，过点 P 作 PE∥AC 交 DC 于点 E，同时，点 Q 从点 C 出发沿 CB 方向，在射线 CB 上匀速运动，速度是 2 cm/s，连接 PQ，QE，PQ 与 AC 交与点 F，设运动时间为 ts0（1）当 t 为何值时，四边形 PFCE 是平行四边形；
（2）设 △PQE 的面积为 Scm2，求 S 与 t 的函数关系式；
（3）是否存在某一时刻 t，使得 △PQE 的面积为矩形 ABCD 面积的 932；
（4）是否存在某一时刻 t，使得点 E 在线段 PQ 的垂直平分线上．
答案
第一部分
1. C
2. B
3. A
4. B
5. D
6. A
7. B
8. D
第二部分
9. k>−94 且 k≠0
【解析】∵ 关于 x 的一元二次方程 kx2−3x−1=0 有两个不相等的实数根，
∴k≠0 且 Δ>0，即 −32−4×k×−1>0，
解得：k>−94 且 k≠0．
10. 20%
11. 5.5
12. −5,4
13. 15
14. 8n−4
第三部分
15. 仅思路：
（1）作 ∠C 的角平分线，交 AB 于 D 点；
（2）过 D 作 DE⊥BC 于 E，作 DF⊥AC 于 F；
（3）四边形 CEDF 即为所求的正方形．
16. （1） x1=−61+16，x2=61−16．
（2） x1=3，x2=1．
17. 这个游戏对双方公平，理由：
列表如下：
123412345234563456745678
共有 16 种情况，每种情况出现的可能性相同．
P小颖胜=616=38，P小丽胜=616=38，
所以这个游戏对双方公平．
18. 将 x=2+3 代入原方程得：2+32−42+3+c=0．
解得 c=1．
∴ 原方程为 x2−4x+1=0，解得 x1=2+3，x2=2−3．
∴ 方程的另一根为 2−3，c 的值为 1．
19. 设平行于围墙的一段长为 x m，
则垂直于围墙的一段长为 50−x2 m，
所以 x⋅50−x2=300，
解得 x1=20，x2=30（舍），
50−202=15，
故砌墙时平行于围墙的一段长 20 m，垂直于墙的段长为 15 m 时符合题目要求．
20. 过 A 作 AM⊥BC 于 M，交 DG 于 N，
则 AM 为 △ABC 边 BC 上的高，AN 为 △ADG 边 DG 上的高．
S△ABC=12AB⋅AC=12BC⋅AM，BC=AB2+AC2=2.5，
即 12×2×1.5=12×2.5×AM，解得 AM=1.2．
∵ 四边形 DEFG 为矩形，
∴DG∥BC，
∴∠ADG=∠ABC，∠AGD=∠ACB，
∴△ADG∽△ABC，
∴ANAM=DGBC，即 1.2−DE1.2=2DE2.5，解得 DE=3049，
∴DG=6049．
∴ 矩形 DEFG 的长和宽分别是 6049 米和 3049 米．
21. （1） ∵ 四边形 ABCD 为平行四边形，
∴AB=CD，AB∥CD，
∴∠ABE=∠CDF，∠BAD=∠BCD，
∵MA⊥AN，NC⊥BC，
∴∠BAM=∠DCN，
在 △ABE 和 △CDF 中，
∠ABE=∠CDF,AB=CD,∠BAM=∠DCN,
∴△ABE≌△CDF（ASA）．
（2） 当四边形 ABCD 为菱形时（或当 AB=BC 时等），四边形 AECF 是菱形．
∵△ABE≌△CDF，
∴AE=CF，
∵MA⊥AN，NC⊥BC，
∴AM∥CN，
∴ 四边形 AECF 为平行四边形，
∵ 四边形 ABCD 是菱形，
∴AC⊥EF，
∴ 四边形 AECF 为菱形．
22. 由题意，设 y=kx+b，
当 x=10 时，y=100；
当 x=12 时，y=80，
所以 100=10k+b,80=12k+b,
解得 k=−10，b=200，
所以 y=−10x+200，
所以 x−8−10x+200=320，
解得 x1=12，x2=16，
当销售单价 x=12 时，销售量 y=80，
当销售单价 x=16 时，销售量 y=−10×16+200=40，不符合题意．
所以销售单价为 12 元/千克时，该超市销售这种水果每天获取的利润为 320 元．
23. （1） 是
（2） ∠B=3∠C；∠B=n∠C
（3） 60∘ 和 105∘
（4） 160∘ 和 10∘
【解析】由题意另外两个角均为 10∘ 的正整数倍，且互相存在正整数倍关系，
设另外两个角分别为 10α 和 10β，且 10α=n⋅10β，α，β，n 均为正整数，
因为 10α+10β+10∘=180∘，
即 n⋅10β+10β+10∘=180∘，
所以 n+1β=17，
因为 α，β，n 均为正整数，
所以 n+1=17,β=1,
所以 n=16，β=1，
所以 10α=n⋅10β=160∘，10β=10∘，
所以另外两个角的度数分别为 160∘ 和 10∘．
24. （1） 当四边形 PFCE 是平行四边形时，PF∥CE，
又 ∵PD∥QC，
∴ 四边形 CDPQ 为平行四边形，
∴PD=CQ，即 8−t=2t，
∴t=83．
（2） ∵PE∥AC，
∴DPDA=DEDC，即 8−t8=DE6，
∴DE=6−34t，
∴CE=6−6+34t=34t，
∴S△PDE=12PD⋅DE=128−t6−34t=38t2−6t+24，
S△CEQ=12CE⋅CQ=12×34t×2t=34t2，
S梯形CDPQ=12QC+PD⋅CD=122t+8−t⋅6=3t+24，
∴S=S梯形CDPQ−S△PDE−S△CEQ=−98t2+9t0 （3） 由题意，−98t2+9t=932×8×6，解得 t1=2，t2=6．
∴ 当 t=2 s 或 6 s 时，△PQE 的面积为矩形 ABCD 面积的 932．
（4） 当点 E 在线段 PQ 的垂直平分线上时，EQ=PE，
∴EQ2=PE2．
在 Rt△CEQ 中，CE2+CQ2=EQ2；
在 Rt△PDE 中，PD2+DE2=PE2．
∴CE2+CQ2=PD2+DE2，
即 34t2+2t2=8−t2+6−34t2，
解得 t1=573−256，t2=−573+256（舍）．
∴ 当 t=573−256 时，点 E 在线段 PQ 的垂直平分线上．