
2019-2020学年广东省佛山市高明区八下期末数学试卷
展开一、选择题(共10小题;共50分)
1. 下列图形中是中心对称图形的是
A. B.
C. D.
2. 若 x>y,则下列式子中正确的是
A. x−3
3. 使分式 xx−2 有意义的条件是
A. x≠2B. x≠−2C. x≠±2D. x=2
4. 下列等式从左到右变形中,属于因式分解的是
A. ax+y=ax+ayB. x2−2x+1=xx−2+1
C. x+3x−3=x2−9D. x2−1=x+1x−1
5. 计算:x2yx−y⋅x−yxy=
A. xB. yxC. yD. 1x
6. 若一个多边形的内角和是 720∘,则这个多边形的边数为
A. 4B. 5C. 6D. 7
7. 如图,在平行四边形 ABCD 中,AD=6,点 E,F 分别是 BD,CD 的中点,则 EF=
A. 2B. 3C. 4D. 5
8. 如图,在 △ABC 中,AB=AC,D 是 BC 的中点,∠B=35∘,则 ∠BAD=
A. 110∘B. 70∘C. 55∘D. 35∘
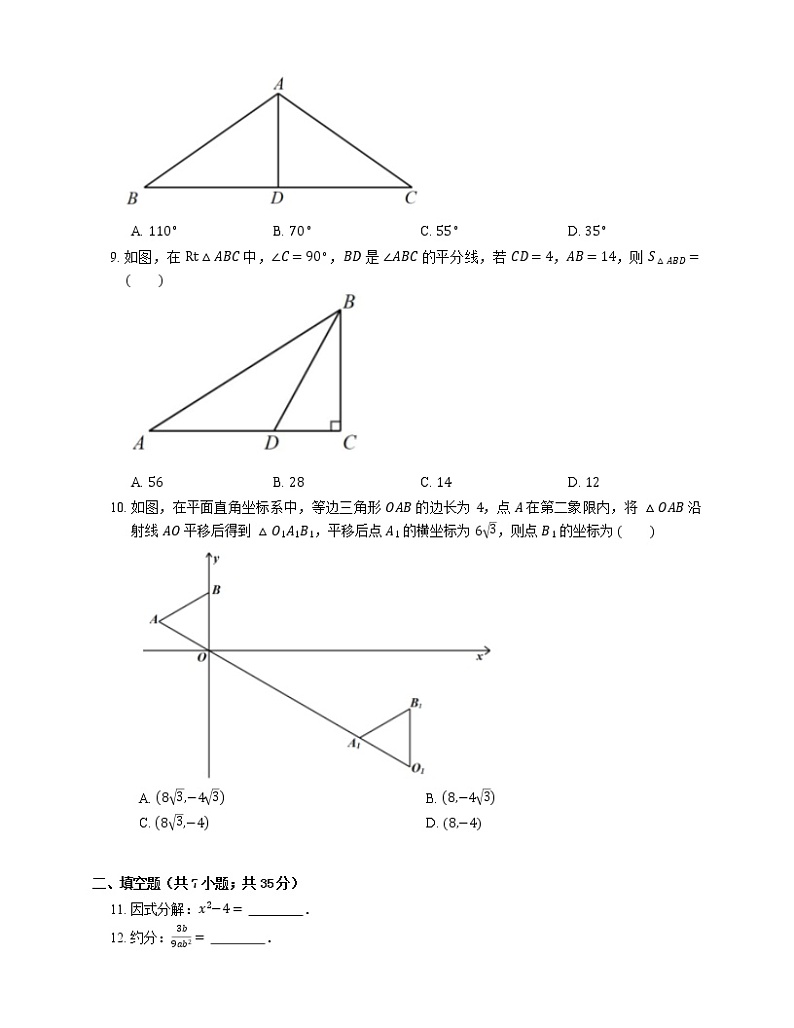
9. 如图,在 Rt△ABC 中,∠C=90∘,BD 是 ∠ABC 的平分线,若 CD=4,AB=14,则 S△ABD=
A. 56B. 28C. 14D. 12
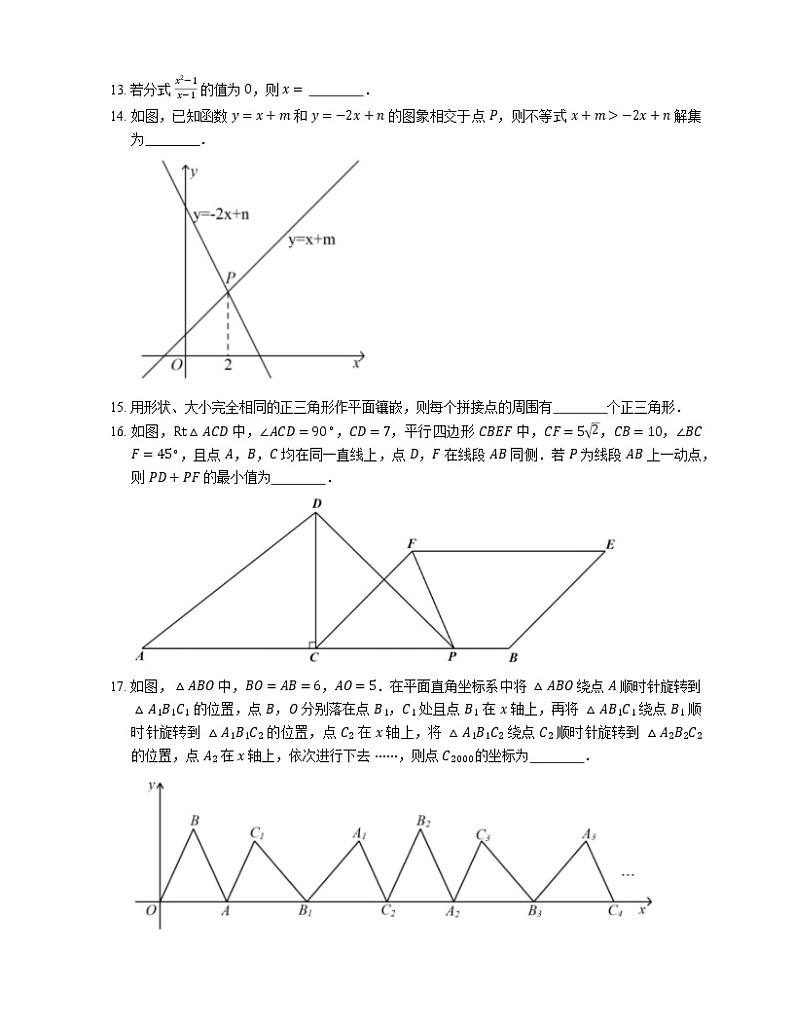
10. 如图,在平面直角坐标系中,等边三角形 OAB 的边长为 4,点 A 在第二象限内,将 △OAB 沿射线 AO 平移后得到 △O1A1B1,平移后点 A1 的横坐标为 63,则点 B1 的坐标为
A. 83,−43B. 8,−43
C. 83,−4D. 8,−4
二、填空题(共7小题;共35分)
11. 因式分解:x2−4= .
12. 约分:3b9ab2= .
13. 若分式 x2−1x−1 的值为 0,则 x= .
14. 如图,已知函数 y=x+m 和 y=−2x+n 的图象相交于点 P,则不等式 x+m>−2x+n 解集为 .
15. 用形状、大小完全相同的正三角形作平面镶嵌,则每个拼接点的周围有 个正三角形.
16. 如图,Rt△ACD 中,∠ACD=90∘,CD=7,平行四边形 CBEF 中,CF=52,CB=10,∠BCF=45∘,且点 A,B,C 均在同一直线上,点 D,F 在线段 AB 同侧.若 P 为线段 AB 上一动点,则 PD+PF 的最小值为 .
17. 如图,△ABO 中,BO=AB=6,AO=5.在平面直角坐标系中将 △ABO 绕点 A 顺时针旋转到 △A1B1C1 的位置,点 B,O 分别落在点 B1,C1 处且点 B1 在 x 轴上,再将 △AB1C1 绕点 B1 顺时针旋转到 △A1B1C2 的位置,点 C2 在 x 轴上,将 △A1B1C2 绕点 C2 顺时针旋转到 △A2B2C2 的位置,点 A2 在 x 轴上,依次进行下去 ⋯⋯,则点 C2000 的坐标为 .
三、解答题(共8小题;共104分)
18. 解不等式组:2x−1
19. 解分式方程:x−8xx−1+3x−1=0.
20. 如图,Rt△ABC 中,∠C=90∘,∠A=30∘.
(1)作 AB 边上的垂直平分线 DE,交 AC 于点 D,交 AB 于点 E(用尺规作图,保留作图痕迹,不要求写作法);
(2)连接 BD,若 AD=8 cm,则 CD= cm,S△BCD= cm2.
21. △ABC 在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为 1 个单位长度.按要求作图:
(1)将 △ABC 向下平移 6 个单位长度得到 △A1B1C1,画出 △A1B1C1;
(2)画出 △ABC 关于原点 O 的中心对称图形 △A2B2C2;
(3)△A1B1C1 与 △A2B2C2 关于点 P 成中心对称,则点 P 的坐标为 .
22. 先化简,再求值:1−1x+1÷x2−xx2+2x+1,从 −1,0,1,2 中选择一个合适的数代入求值.
23. 在抗击新冠肺炎疫情期间,市场上的消毒液和防护口罩热销.某药店推出两种优惠方案,方案①:购买 1 瓶消毒液,赠送 1 个口罩,方案②:消毒液和口罩一律按 9 折优惠.消毒液每瓶定价 40 元,口罩每个定价 5 元.小明需买 4 瓶消毒液和若干个口罩(不少于 4 个),设购买口罩 x 个,用优惠方案①购买费用为 y1 元,用优惠方案②购买费用为 y2 元.
(1)请分别写出 y1,y2 与 x 之间的函数关系式;
(2)什么情况下选择方案②更优惠?
(3)若要买 4 瓶消毒液和 12 个口罩,请你设计怎样购买最便宜.
24. 如图 1,已知平行四边形 ABCD 中,AC=AD,AE⊥CD 于点 E,BF⊥AC 分别交 AC,AE 于点 G,F 且 BF=AD.
(1)求证:△ABF≌△EAD;
(2)如图 2,连接 BE,求证:F 是 AE 的中点;
(3)如图 2,连接 CF,求证:BE⊥CF.
25. 如图,在平面直角坐标系中,直线 y=−12x+3 与 x 轴、 y 轴相交于 A,B 两点,点 C 在线段 OA 上,将线段 CB 绕着点 C 顺时针旋转 90∘ 得到线段 CD,此时点 D 恰好落在直线 AB 上,过点 D 作 DE⊥x 轴于点 E.
(1)求证:△BOC≌△CED;
(2)请直接写出点 D 的坐标,并求出直线 BC 的函数关系式;
(3)若点 P 是 x 轴上的一个动点,点 Q 是线段 CB 上的点(不与点 B,C 重合),是否存在以 C,D,P,Q 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的 P 点坐标.若不存在,请说明理由.
答案
第一部分
1. D
2. B
3. A
4. D
5. A
6. C
7. B
8. C
9. B
10. C
第二部分
11. x+2x−2
12. 13ab
13. −1
14. x>2
15. 6
16. 13
17. 17000,0
第三部分
18.
2x−1
x<3.
解不等式 ② 得:
x≥−1.∴
原不等式组的解集为
−1≤x<3.
19. 方程两边同乘 xx−1 得:
x−8+3x=0.
解得
x=2.
经检验,x=2 是原方程的根.
20. (1) 如图所示.
∴DE 为所求.
(2) 4;83
21. (1)∴ 如图,△A1B1C1 为所求;
(2)∴ 如图,△A2B2C2 为所求;
(3)0,−3
22. 原式=x+1x+1−1x+1⋅x+12xx−1=xx+1⋅x+12xx−1=x+1x−1.
当 x=2 时,原式=3.
23. (1) y1=40×4+5x−4=5x+140,
y2=40×0.9×4+5×0.9x=4.5x+144.
(2) 当 y1>y2 时,5x+140>4.5x+144,
解得 x>8,
答:当 x>8 时,选方案②更优惠.
(3) 方案①:y1=5×12+140=200(元),
方案②:y2=4.5×12+144=198(元),
方案③:先按方案①买 4 瓶消毒液,送 4 个口罩,剩下 8 个口罩按方案②打九折购买,总价为:40×4+5×0.9×8=196(元),
因为 200>198>196,
所以方案③最省钱.
答:购买 4 瓶消毒液和 12 个口罩用方案③最优惠.
24. (1) 因为 AC=AD,AE⊥CD,
所以 ∠1=∠2,∠2+∠D=90∘,
因为 BG⊥AC,
所以 ∠1+∠3=90∘,
所以 ∠3=∠D.
在平行四边形 ABCD 中,AB∥CD,
所以 ∠BAF=∠AED=90∘,
因为 ∠BAF=∠AED,∠3=∠D,BF=AD,
所以 △ABF≌△EAD(AAS).
(2) 由(1)得,△ABF≌△EAD,
所以 AB=AE,AF=DE,
因为四边形 ABCD 是平行四边形,
所以 CD=AB=AE,
因为 AC=AD,AE⊥CD,
所以 DE=12CD,
所以 AF=DE=12CD=12AE,
所以 F 是 AE 中点.
(3) 因为四边形 ABCD 是平行四边形,BF=AD,
所以 BC=AD=BF,
由(2)得:DE=12CD,AF=12AE,
所以 CE=12CD,EF=12AE,
又因为 AE=CD,
所以 CE=EF,
所以 BE 垂直平分 CF,
所以 BE⊥CF.
25. (1) 由题意得:∠BOC=∠BCD=∠CED=90∘,BC=CD,
因为 ∠1+∠2=90∘,∠2+∠3=90∘,
所以 ∠1=∠3,
又因为 ∠BOC=∠CED,BC=CD,
所以 △BOC≌△CED(AAS).
(2) D 点的坐标为 4,1,
在 y=−12x+3 中令 x=0,可得 y=3,
所以 B 点坐标为 0,3.
由(1)得 △BOC≌△CED,
所以 OC=DE=1,C 点坐标为 1,0,
设直线 BC 的表达式为 y=kx+b,
所以 3=b,0=k+b,
解得 k=−3,b=3.
所以直线 BC 的表达式为 y=−3x+3.
(3) P−73,0 或 P133,0.
2019-2020学年广东省佛山市高明区九年级(上)期末数学试卷: 这是一份2019-2020学年广东省佛山市高明区九年级(上)期末数学试卷,共1页。试卷主要包含了解答题等内容,欢迎下载使用。
2019-2020学年广东省佛山市南海区八下期末数学试卷: 这是一份2019-2020学年广东省佛山市南海区八下期末数学试卷,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2019-2020学年广东省佛山市禅城区八下期末数学试卷: 这是一份2019-2020学年广东省佛山市禅城区八下期末数学试卷,共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












