2019-2020学年山东青岛莱西市八上期末数学试卷（五四制）

这是一份2019-2020学年山东青岛莱西市八上期末数学试卷（五四制），共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 3 的相反数是
A. 3B. −3C. ±3D. 33

2. 下列倡导节约的图案中，是轴对称图形的是
A. B.
C. D.

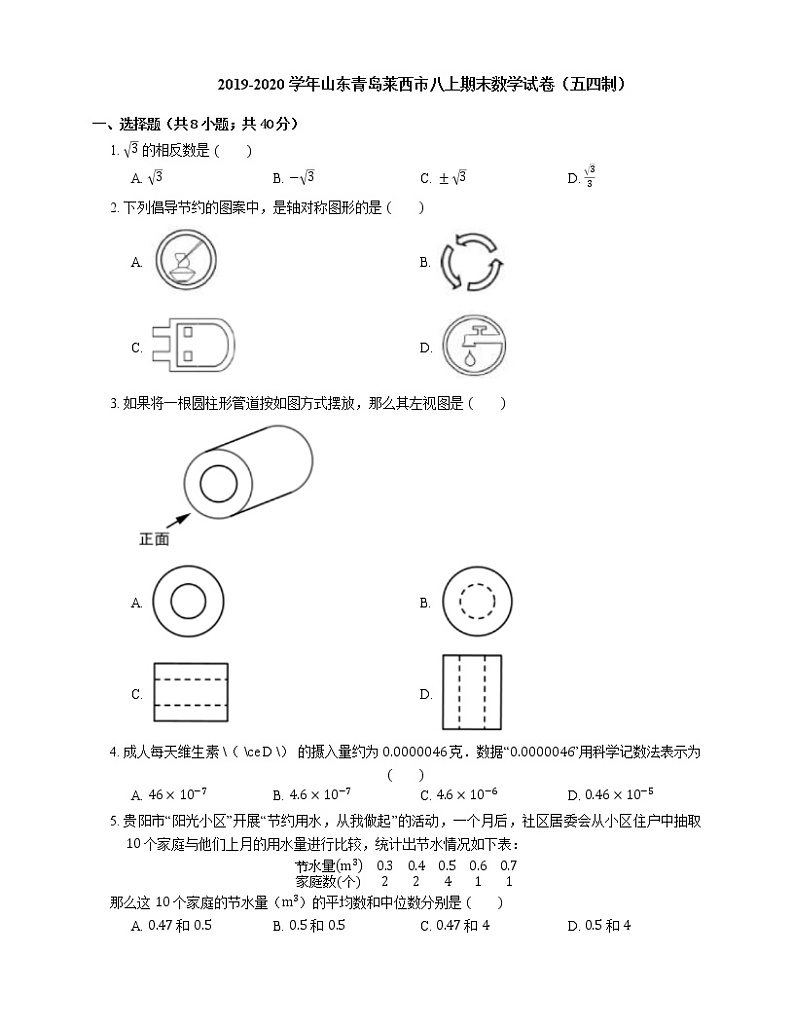
3. 如果将一根圆柱形管道按如图方式摆放，那么其左视图是
A. B.
C. D.

4. 成人每天维生素 \（ \ce D \） 的摄入量约为 0.0000046 克．数据“0.0000046”用科学记数法表示为
A. 46×10−7B. 4.6×10−7C. 4.6×10−6D. 0.46×10−5

5. 贵阳市“阳光小区”开展“节约用水，从我做起”的活动，一个月后，社区居委会从小区住户中抽取 10 个家庭与他们上月的用水量进行比较，统计出节水情况如下表：
节水量家庭数个22411
那么这 10 个家庭的节水量（m3）的平均数和中位数分别是
A. 0.47 和 0.5B. 0.5 和 0.5C. 0.47 和 4D. 0.5 和 4

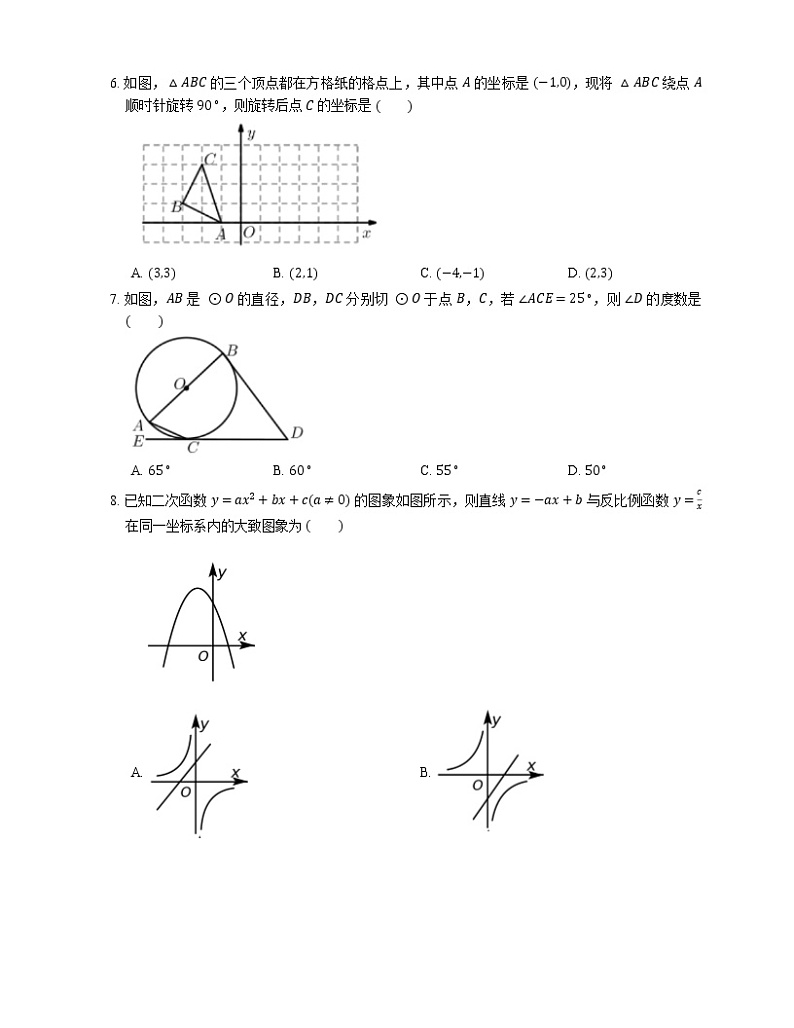
6. 如图，△ABC 的三个顶点都在方格纸的格点上，其中点 A 的坐标是 −1,0，现将 △ABC 绕点 A 顺时针旋转 90∘，则旋转后点 C 的坐标是
A. 3,3B. 2,1C. −4,−1D. 2,3

7. 如图，AB 是 ⊙O 的直径，DB，DC 分别切 ⊙O 于点 B，C，若 ∠ACE=25∘，则 ∠D 的度数是
A. 65∘B. 60∘C. 55∘D. 50∘

8. 已知二次函数 y=ax2+bx+ca≠0 的图象如图所示，则直线 y=−ax+b 与反比例函数 y=cx 在同一坐标系内的大致图象为
A. B.
C. D.

二、填空题（共6小题；共30分）
9. 计算：12⋅cs30∘−−120= ．

10. 某活动小组购买了 4 个篮球和 5 个足球，一共花费了 435 元，其中篮球的单价比足球的单价多 3 元，求篮球的单价和足球的单价．设篮球的单价为 x 元，足球的单价为 y 元，依题意，可列方程组为 ．

11. 若二次函数 y=x2−12x+b+1 与 x 轴没有交点，则 b 取值范围为 ．

12. 如图，在平面直角坐标系 xOy 中，点 A，P 分别在 x 轴、 y 轴上，∠APO=30∘．先将线段 PA 沿 y 轴翻折得到线段 PB，再将线段 PA 绕点 P 顺时针旋转 30∘ 得到线段 PC，连接 BC．若点 A 的坐标为 −1,0，则线段 BC 的长为 ．

13. 如图，∠AOB=90∘，∠B=30∘，以点 O 为圆心，OA 为半径作弧交 AB 于点 A，点 C，交 OB 于点 D，若 OA=1，则阴影部分的面积为 ．

14. 如图，有 6 个棱长分别是 3 cm，4 cm，5 cm 的相同的长方体，第一个长方体的一个面染色、第二个长方体的两个面染色、第三个长方体的三个面染色 ⋯⋯ 依次下去，将第六个长方体的六个面染色，染色后把所有长方体分割成棱长为 1 厘米的小正方体，分割完毕后，恰好只有一面是红色的小正方体最多有 个．

三、解答题（共11小题；共143分）
15. 用直尺、圆规作图，不写作法，但要保留作图痕迹．
如图，△ABC 中，∠ABC=90∘，请在 BC 边上找一点 P，作圆 P 与 AC，AB 都相切．

16. 2m+nm2−mn+1m⋅m2−n2．

17. 解不等式组：3x+1<5x,13x−1≤7−53x.

18. 为弘扬中华传统文化，某校开展“汉剧进课堂”的活动．该校随机抽取部分学生，按四个类别：A表示“很喜欢”，B表示“喜欢”，C表示“一般”，D表示“不喜欢”，调查他们对汉剧的喜爱情况，将结果绘制成如下两幅不完整的统计图，根据图中提供的信息，解决下列问题．
（1）这次共抽取 名学生进行调查统计，扇形统计图中，D类所对应的扇形圆心角的大小是 ．
（2）将条形统计图补充完整．
（3）该校共有 1500 名学生，估计该校表示“喜欢”的B类的学生大约有多少人?

19. 某商场举办抽奖活动，规则如下：在不透明的袋子中有 2 个红球和 2 个黑球，这些球除颜色外都相同，顾客每次摸出一个球，若摸到红球，则获得 1 份奖品，若摸到黑球，则没有奖品．
（1）如果小芳只有一次摸球机会，那么小芳获得奖品的概率为 ．
（2）如果小芳有两次摸球机会（摸出后不放回），求小芳获得 2 份奖品的概率．

20. 鲁南高铁临沂段修建过程中需要经过一座小山．如图，施工方计划沿 AC 方向开挖隧道，为了加快施工速度，要在小山的另一侧 D（A，C，D 共线）处同时施工．测得 ∠CAB=30∘，AB=4 km，∠ABD=105∘，求 BD 的长．

21. 某小微企业为加快产业转型升级步伐，引进一批 A，B 两种型号的机器．已知一台 A 型机器比一台 B 型机器每小时多加工 2 个零件，且一台 A 型机器加工 80 个零件与一台 B 型机器加工 60 个零件所用时间相等．
（1）每台 A，B 两种型号的机器每小时分别加工多少个零件?
（2）如果该企业计划安排 A，B 两种型号的机器共 10 台一起加工一批该零件，为了如期完成任务，要求两种机器每小时加工的零件不少于 72 件，两种机器耗材不同，A 型机器加工一个零件成本为 30 元，B 型机器加工一个零件成本为 20 元，怎样安排两种机器数量能使每小时的总加工成本最小?

22. 如图，某拦河坝横截面原设计方案为梯形 ABCD，其中 AD∥BC，∠ABC=72∘，为了提高拦河坝的安全性，现将坝顶宽度水平缩短 10m，坝底宽度水平增加 4m，使 ∠EFC=45∘，请你计算这个拦河大坝的高度．（参考数据：sin72∘≈1213，cs72∘≈513，tan72∘≈125）

23. 2018 年非洲猪瘟疫情暴发后，专家预测，2019 年我市猪肉售价将逐月上涨，每千克猪肉的售价 y1（元）与月份 x（1≤x≤12，且 x 为整数）之间满足一次函数关系，如下表所示，每千克猪肉的成本 y2（元）与月份 x（1≤x≤12，且 x 为整数）之间满足二次函数关系，且 3 月份每千克猪肉的成本全年最低，为 9 元，如图所示．
月份x⋯3456⋯售价y1/元⋯12141618⋯
（1）求 y1 与 x 之间的函数关系式．
（2）求 y2 与 x 之间的函数关系式．
（3）设销售每千克猪肉所获得的利润为 w（元），求 w 与 x 之间的函数关系式，哪个月份销售每千克猪肉所获得的利润最大?最大利润是多少元?

24. 我们已经知道，形如 ca±b 的无理数的化简要借助平方差公式：
例如：32−3=3×2+32−32+3=6+3322−32=6+334−3=6+33．
下面我们来看看完全平方公式在无理数化简中的作用．
问题提出：7+43 该如何化简?
建立模型：形如 m±2n 的化简，只要我们找到两个数 a，b，使 a+b=m，ab=n，这样 a2+b2=m，a⋅b=n．
那么便有：m±2n=a±b2=a±ba>b．
问题解决：化简 7+43，
解：首先把 7+43 化为 7+212，这里 m=7，n=12，由于 4+3=7，4×3=12，
即 42+32=7，4×3=12，
∴7+43=7+212=4+32=2+3．
（1）模型应用 1：
利用上述解决问题的方法化简下列各式．
① 3+22．
② 11−46．
（2）模型应用 2：
在 Rt△ABC 中，∠C=90∘，AB=4−3，AC=3，那么 BC 边的长为多少?（结果化成最简）

25. 已知：如图，在矩形 ABCD 中，AC 是对角线，AB=6cm，BC=8cm．点 P 从点 D 出发，沿 DC 方向匀速运动，速度为 1cm/s，同时，点 Q 从点 C 出发，沿 CB 方向匀速运动，速度为 2cm/s，过点 Q 作 QM∥AB 交 AC 于点 M，连接 PM，设运动时间为 ts0（1）当 t 为何值时，∠CPM=90∘．
（2）是否存在某一时刻 t，使 S四边形MQCP=1532S矩形ABCD?若存在，求出 t 的值；若不存在，请说明理由．
（3）当 t 为何值时，点 P 在 ∠CAD 的角平分线上．
答案
第一部分
1. B
2. C【解析】A、不是轴对称图形，故此选项错误；
B、不是轴对称图形，故此选项错误；
C、是轴对称图形，故此选项正确；
D、不是轴对称图形，故此选项错误．
故选：C．
3. C【解析】左视图为长方形，且有两条虚线，
∴ C选项符合题意，故C正确．
4. C【解析】0.0000046=4.6×10−6．
5. A
【解析】这 10 个数据的平均数为 0.3×2+0.4×2+0.5×4+0.6×1+0.7×110=0.47，
中位数为 0.5+0.52=0.5．
6. B【解析】如图，
△ABC 绕点 A 顺时针旋转 90∘ 得到 △ABʹCʹ，旋转后点 C 的坐标为 2,1．
7. D【解析】连接 BC，
∵DB，DE 分别切 ⊙O 于点 B，C，
∴BD=DC，
∵∠ACE=25∘，
∴∠ABC=25∘，
∵AB 是 ⊙O 的直径，
∴∠ACB=90∘，
∴∠DBC=∠DCB=90∘−25∘=65∘，
∴∠D=50∘．
8. D【解析】二次函数开口朝下，
∴a<0，
交 y 轴于正半轴，
∴c>0，
对称轴在 x 轴负半轴，
x=−b2a<0，
又 ∵a<0，
∴b<0，
∴ 由二次函数图象易知：a<0，b<0，c>0，
∴y=−ax+b 中，−a>0，b<0，
一次函数经过一，三，四象限，
y=cx，c>0，
∴ 反比例函数经过一，三象限，
∴ D选项符合题意，故D正确．
第二部分
9. 2
【解析】原式=23⋅32−1=2.
10. 4x+5y=435,x−y=3
11. b>−1516
【解析】∵ 二次函数与 x 轴无交点，
即 y=0 无解，
即 x2−12x+b+1=0 无解，
∴Δ=b2−4ac=−122−4×1×b+1=14−4b−4=14−164−4b=−154−4b<0，
∴−154<4b，
∴b>−154×14=−1516，
∴ b 的取值范围是：b>−1516．
12. 22
【解析】根据题意可知，PA=PB=PC，
∵∠APO=30∘，由对称及旋转可知，∠CPB=90∘，
在 Rt△AOP 中，AO=1，
∴AP=2，
∴ 在 Rt△BCP 中，BC=22．
13. π12
【解析】连接 OC，作 CH⊥OB 于 H，
∵∠AOB=90∘，∠B=30∘，
∴∠OAB=60∘，AB=2OA=2，
由勾股定理得，OB=AB2−OA2=22−12=3，
∵OA=OC，∠AOB=60∘，
∴△AOC 为等边三角形，
∴∠AOC=60∘，
∴∠COB=30∘，
∴CO=CB，CH=12OC=12OA=12，
∴阴影部分的面积=60π×12360−12×1×1×32+12×3×12−30π×12360∘=π6−34+34−π12=π12.
故答案为：π12．
14. 177
【解析】（1）一面是红色的正方体上一面涂色的有：
5×4=20（个），
（2）两面是红色的正方体上一面涂色的有：
5×4×2=40（个），
（3）三面是红色的正方体上一面涂色的有：
5−1×4×2+3−1−1×4=36（个），
（4）四面是红色的正方体上一面涂色的有：
5−1−1×4×2+3−1−1×4×2=32（个），
（5）五面是红色的正方体上一面涂色的有：
5−1−1×4−1×2+3−1−1×4−1×2+5−1−1×3−1−1=27个,
（6）六面是红色的正方体上一面涂色的有：
5−1−1×4−1−1×2+3−1−1×4−1−1×2+5−1−1×3−1−1×2=22个,
一共一面涂色的有小正方体的个数是：
20+40+36+32+27+22=177（个）．
第三部分
15. 尺规作图——作一个角的平分线．
如答图所示，点 P 即为所求作的点．
16. 原式=2m+n+m−nmm−n⋅m+nm−n=3mmm−n⋅m+nm−n=3m+n=3m+3n.
故答案为：3m+3n．
17.
3x+1<5x, ⋯⋯①13x−1≤7−53x, ⋯⋯②
由①得：
x>32;
由②得：
x≤4,
则不等式组的解集为 3218. （1） 50；72∘
【解析】这次共抽取：12÷24%=50（人），
D类所对应的扇形圆心角的大小 360∘×1050=72∘．
（2） A类学生：50−23−12−10=5（人），
条形统计图补充如下：
（3） 该校表示“喜欢”的B类的学生大约有 1500×2350=690（人），
答：该校表示“喜欢”的B类的学生大约有 690 人．
19. （1） 12
【解析】从布袋中任意摸出 1 个球，摸出是红球的概率 =24=12．
（2） 画树状图为：
共有 12 种等可能的结果数，其中两次摸到红球的结果数为 2，
两次摸到红球的概率 =212=16．
20. 作 BE⊥AD 于点 E，
∵∠CAB=30∘，AB=4 km，
∴∠ABE=60∘，BE=2 km，
∵∠ABD=105∘，
∴∠EBD=45∘，
∴∠EDB=45∘，
∴BE=DE=2 km ，
∴BD=22+22=22 km，
即 BD 的长是 22 km．
21. （1） 设每台 B 型机器每小时加工 x 个零件，则每台 A 型机器每小时加工 x+2 个零件，
依题意得：
80x+2=60x.
解得：
x=6.
经检验，x=6 是原方程的解，
∴x+2=8．
答：每台 A 型机器每小时加工 8 个零件，每台 B 型机器每小时加工 6 个零件．
（2） 设 A 型机器安排 m 台，则 B 型机器安排 10−m 台，
依题意，得：
8m+610−m≥72.
解得：
m≥6.
设总加工成本为 y 元，由题意得：
y=8m×30+610−m×20=120m+1200，
∵k=120>0，
∴y 随 m 的增大而增大，
∴ 当 m=6 时，y 最小，此时 10−m=4（台）．
答：安排 6 台 A 型机器，4 台 B 型机器可使总费用最少．
22. 过点 A 作 AM⊥CF 于点 M，过点 E 作 EN 垂直 CF 于点 N，
设拦河大坝的高度为 xm，
在 Rt△ABM 和 Rt△EFN 中，
∵∠ABM=72∘，∠EFC=45∘，
∴BM=AMtan∠ABM=x125=5x12，FN=x，
∵AE=10m，BF=4m，FN−AE=BF+BM，
∴x−10=4+5x12，解得：x=24．
答：拦河大坝的高度为 24m．
23. （1） 设 y1 与 x 之间的函数关系式为 y1=kx+b，
将 3,124,14 代入 y1 得，3k+b=12,4k+b=14,
解得：k=2,b=6.
∴y1 与 x 之间的函数关系式为：y1=2x+6．
（2） 由题意得，抛物线的顶点坐标为 3,9，
∴ 设 y2 与 x 之间的函数关系式为：y2=ax−32+9，
将 5,10 代入 y2=ax−32+9 得 a5−32+9=10，
解得：a=14，
∴y2=14x−32+9=14x2−32x+454．
（3） 由题意得，
w=y1−y2=2x+6−14x2+32x−454=−14x2+72x−214,
∵−14<0，
∴w 有最大值，
∴ 当 x=−b2a=−722×−14=7 时，
w最大=−14×72+72×7−214=7．
24. （1） ①
3+22=12+22+21×2=1+22=1+2=1+2.
②
11−46=11−224=32+82−23×8=3−82=∣3−8∣=22−3.
（2） BC=AB2−AC2=4−32−32=16−83=16−248=122+42−212×4=12−42=12−4=23−2.
25. （1） 由题意知 QC=2t，DP=t，
∴PC=6−t，
当 ∠CPM=90∘ 时，四边形 MQCP 为矩形，
∴MP=QC=2t，
∵∠PCM=∠DCA，∠MPC=∠D=90∘，
∴△CPM∽△CDA，
∴MPAD=CPCD，
∴2t8=6t6，
∴t=2.4．
（2） ∵∠QCM=∠BCA，∠MQC=∠B=90∘，
∴△CQM∽△CBA，
∴MQAB=CQCB，
∴MQ6=2t8，
∴MQ=32t，
过 M 作 MH⊥CD 于点 H，
则四边形 MQCH 为矩形，
∴MH=QC=2t，
∴S四边形MQCP=S△CPQ+S△CPM=12MQ⋅QC+12PC⋅MH=12×32t×2t+126−t×2t=t22+6t,
∵S四边形MQCP=1532S四边形MQCP，
∴t22+6t=1532×6×8，解得 t1=−15（舍），t2=3，
∴t=3s 时，S四边形MQCP=1532S四边形MQCP．
（3） 过 P 作 PN⊥AC 于点 N，
点 P 在 ∠CAD 的平分线上时，PN=PD=t，
在 Rt△PCN 中，sin∠PCN=PNPC=t6t，
在 Rt△DCA 中，AC=AD2+CD2=10，sin∠PCN=ADAC=45，
∴t6t=45，解得 t=83．