
2018-2019学年广东省广州市白云区九年级上期末数学试卷
展开一、选择题(共10小题;共50分)
1. 抛物线 y=−x2 开口方向是
A. 向上B. 向下C. 向左D. 向右
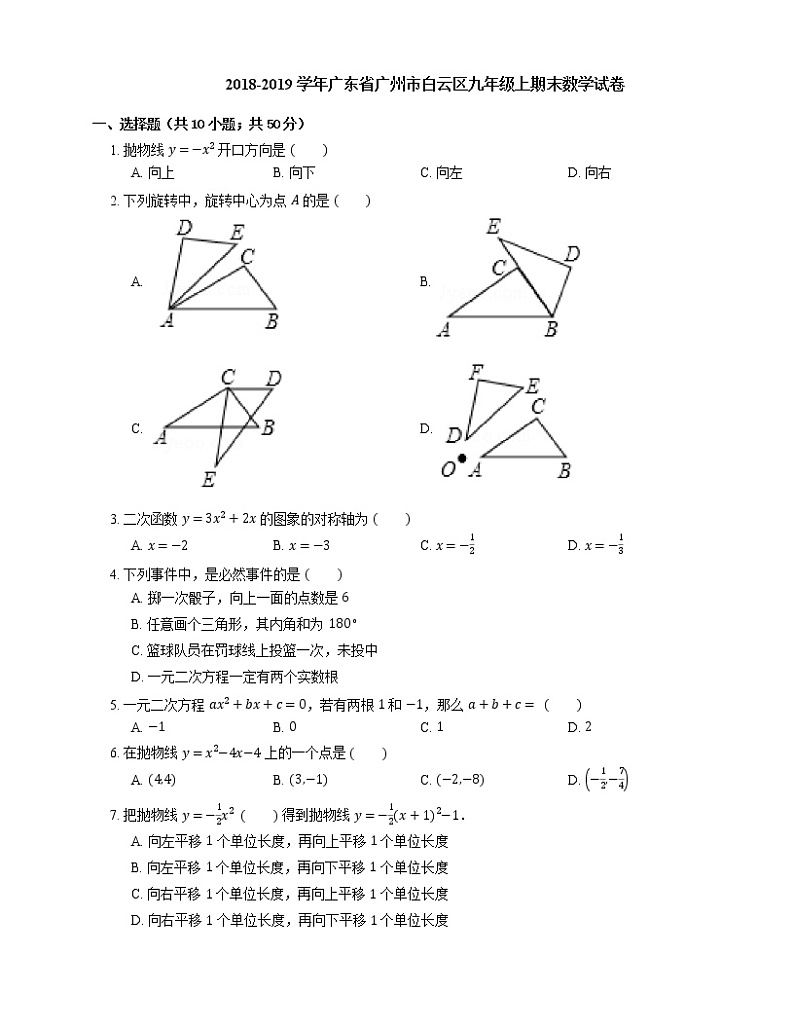
2. 下列旋转中,旋转中心为点 A 的是
A. B.
C. D.
3. 二次函数 y=3x2+2x 的图象的对称轴为
A. x=−2B. x=−3C. x=−12D. x=−13
4. 下列事件中,是必然事件的是
A. 掷一次骰子,向上一面的点数是 6
B. 任意画个三角形,其内角和为 180∘
C. 篮球队员在罚球线上投篮一次,未投中
D. 一元二次方程一定有两个实数根
5. 一元二次方程 ax2+bx+c=0,若有两根 1 和 −1,那么 a+b+c=
A. −1B. 0C. 1D. 2
6. 在抛物线 y=x2−4x−4 上的一个点是
A. 4,4B. 3,−1C. −2,−8D. −12,−74
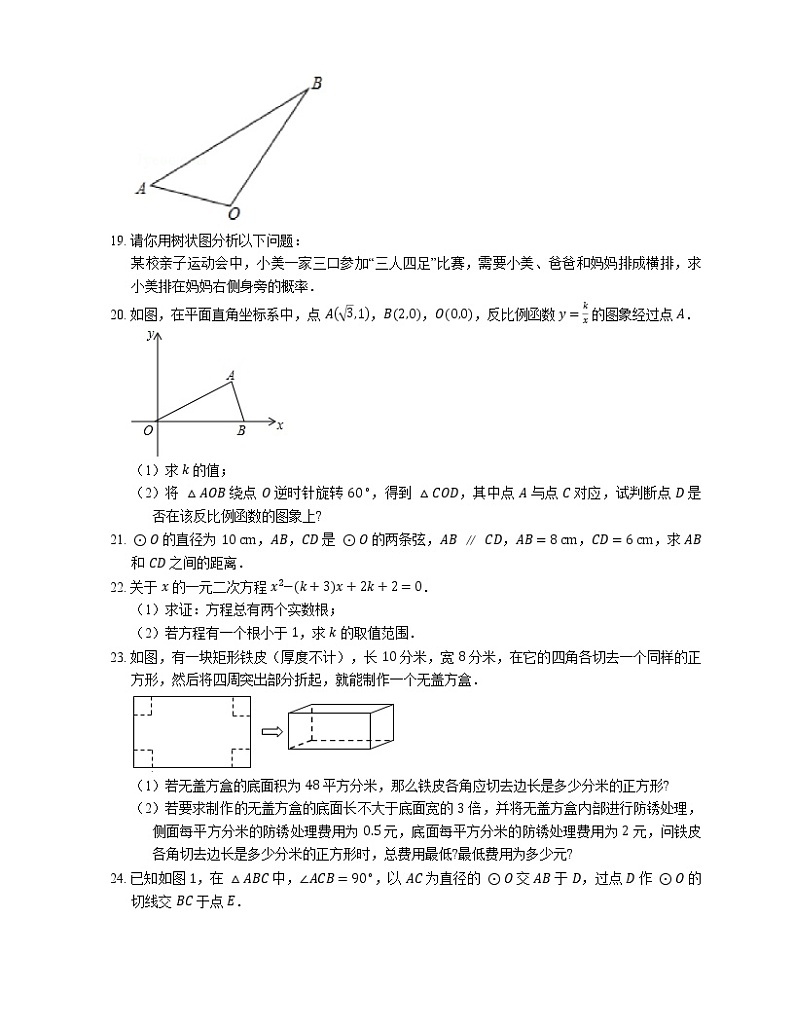
7. 把抛物线 y=−12x2 得到抛物线 y=−12x+12−1.
A. 向左平移 1 个单位长度,再向上平移 1 个单位长度
B. 向左平移 1 个单位长度,再向下平移 1 个单位长度
C. 向右平移 1 个单位长度,再向上平移 1 个单位长度
D. 向右平移 1 个单位长度,再向下平移 1 个单位长度
8. AB,CD 为 ⊙O 的两条不重合的直径,则四边形 ACBD 一定是
A. 等腰梯形B. 矩形C. 菱形D. 正方形
9. 用配方法解下列方程时,配方有错误的是
A. x2+8x+9=0 化为 x+42=25
B. x2−2x−99=0 化为 x−12=100
C. 2t2−7t−4=0 化为 t−742=8116
D. 3x2−4x−2=0 化为 x−232=109
10. 在同一平面直角坐标系中,函数 y=kx 与 y=kxk≠0 的图象大致是
A. (1)(3)B. (1)(4)C. (2)(3)D. (2)(4)
二、填空题(共6小题;共30分)
11. 反比例函数 y=5x 的图象在第 象限.
12. ⊙O 的半径为 10 cm,点 P 到圆心 O 的距离为 12 cm,则点 P 和 ⊙O 的位置关系是 .
13. 当 m 满足条件 时,关于 x 的方程 m2−4x2+mx+3=0 是一元二次方程.
14. 已知函数 y=2x−32+1,当 (填写 x 需满足的条件)时,y 随 x 的增大而增大.
15. 不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,则第一次摸到红球,第二次摸到绿球的概率为 .
16. 某设计运动员在相同的条件下的射击成绩记录如下:
设计次数20401002004001000射中 9 环以上次数153378158321801
根据频率的稳定性,估计这名运动员射击一次“射中 9 环以上”的概率是 .
三、解答题(共9小题;共117分)
17. 解下列方程:x2+x3x−4=0.
18. 画出 △AOB 关于点 O 对称的图形.
19. 请你用树状图分析以下问题:
某校亲子运动会中,小美一家三口参加“三人四足”比赛,需要小美、爸爸和妈妈排成横排,求小美排在妈妈右侧身旁的概率.
20. 如图,在平面直角坐标系中,点 A3,1,B2,0,O0,0,反比例函数 y=kx 的图象经过点 A.
(1)求 k 的值;
(2)将 △AOB 绕点 O 逆时针旋转 60∘,得到 △COD,其中点 A 与点 C 对应,试判断点 D 是否在该反比例函数的图象上?
21. ⊙O 的直径为 10 cm,AB,CD 是 ⊙O 的两条弦,AB∥CD,AB=8 cm,CD=6 cm,求 AB 和 CD 之间的距离.
22. 关于 x 的一元二次方程 x2−k+3x+2k+2=0.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于 1,求 k 的取值范围.
23. 如图,有一块矩形铁皮(厚度不计),长 10 分米,宽 8 分米,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.
(1)若无盖方盒的底面积为 48 平方分米,那么铁皮各角应切去边长是多少分米的正方形?
(2)若要求制作的无盖方盒的底面长不大于底面宽的 3 倍,并将无盖方盒内部进行防锈处理,侧面每平方分米的防锈处理费用为 0.5 元,底面每平方分米的防锈处理费用为 2 元,问铁皮各角切去边长是多少分米的正方形时,总费用最低?最低费用为多少元?
24. 已知如图 1,在 △ABC 中,∠ACB=90∘,以 AC 为直径的 ⊙O 交 AB 于 D,过点 D 作 ⊙O 的切线交 BC 于点 E.
(1)求证:∠B=∠ACD,DE=12BC;
(2)已知如图 2,BG 是 △BDE 的中线,延长 ED 至点 F,使 ED=FD,求证:BF=2BG.
25. 如图,在平面直角坐标系 xOy 中,△ABC 是等腰直角三角形,∠BAC=90∘,A1,0,B0,2,二次函数 y=12x2+bx−2 的图象经过 C 点.
(1)求二次函数的解析式;
(2)平移该二次函数图象的对称轴所在直线 l,若直线 l 恰好将 △ABC 的面积分为 1:2 两部分,请求出此时直线 l 与 x 轴的交点坐标;
(3)将 △ABC 以 AC 所在直线为对称轴翻折 180∘,得到 △ABʹC,那么在二次函数图象上是否存在点 P,使 △PBʹC 是以 BʹC 为直角边的直角三角形?若存在,请求出 P 点坐标;若不存在,请说明理由.
答案
第一部分
1. B【解析】∵a=−1<0,
∴ 抛物线的开口向下.
2. A【解析】A、旋转中心为点 A,符合题意;
B、旋转中心为点 B,不符合题意;
C、旋转中心为 C,不符合题意;
D、旋转中心为 O,不符合题意.
3. D【解析】y=3x2+2x 的对称轴为:直线 x=−22×3=−13.
4. B【解析】A.掷一次骰子,向上一面的点数是 6,属于随机事件;
B.任意画个三角形,其内角和为 180∘,属于必然事件;
C.篮球队员在罚球线上投篮一次未投中,属于随机事件;
D.一元二次方程一定有两个实数根,属于随机事件.
故选:B.
5. B
【解析】把 x=1 代入一元二次方程 ax2+bx+c=0 得:a+b+c=0.
6. D【解析】A、 x=4 时,y=x2−4x−4=−4≠4,点 4,4 不在抛物线上;
B、 x=3 时,y=x2−4x−4=−7≠−1,点 3,−1 不在抛物线上;
C、 x=−2 时,y=x2−4x−4=8≠−8,点 −2,−8 不在抛物线上;
D、 x=−12 时,y=x2−4x−4=−74,点 −12,−74 在抛物线上.
7. B【解析】抛物线 y=−12x2 的顶点坐标为 0,0,抛物线 y=−12x+12−1 的顶点坐标为 −1,−1,
∵ 点 0,0 向左平移 1 个单位,再向下平移 1 个单位得到点 −1,−1,
∴ 把抛物线 y=−12x2 向左平移 1 个单位,再向下平移 1 个单位得到抛物线 y=−12x+12−1.
8. B【解析】连接 AC,BC,BD,AD.
∵AB,CD 为圆 O 的直径,
∴OA=OB,OC=OD,
∴ 四边形 ACBD 为平行四边形,
∵AB=CD,
∴ 四边形 ACBD 是矩形.
9. A【解析】A、 x2+8x+9=0 化为 x+42=7,所以A选项的配方错误;
B、 x2−2x−99=0 化为 x−12=100,所以B选项的配方正确;
C、 2t2−7t−4=0 先化为 t2−72t=2,再化为 t−742=8116,所以C选项的配方正确;
D、 3x2−4x−2=0 先化为 x2−43x=23,再化为 x−232=109,所以D选项的配方正确.
10. B
【解析】当 k>0 时,函数 y=kx 的图象位于一、三象限,y=kxk≠0 的图象位于一、三象限,(1)符合;
当 k<0 时,函数 y=kx 的图象位于二、四象限,y=kxk≠0 的图象位于二、四象限,(4)符合.
第二部分
11. 一、三
【解析】∵k=5>0,
∴ 反比例函数图象分布在第一、三象限.
12. 点 P 在 ⊙O 外
【解析】∵⊙O 的半径 r=10 cm,点 P 到圆心 O 的距离 OP=12 cm,
∴OP>r,
∴ 点 P 在 ⊙O 外.
13. m≠±2
【解析】∵ 关于 x 的方程 m2−4x2+mx+3=0 是一元二次方程,
∴m2−4≠0,即 m≠±2.
14. x≥3(或 x>3)
【解析】∵ 函数 y=2x−32+1,2>0,
∴ 图象开口向上,对称轴为直线 x=3,
∴x≥3(或 x>3)时,y 随 x 的增大而增大.
15. 14
【解析】列表如下:
红绿红红,红绿,红绿红,绿绿,绿
所有等可能的情况有 4 种,
所以第一次摸到红球,第二次摸到绿球的概率 =14.
16. 0.8
【解析】15÷20=0.75,
33÷40=0.825,
78÷100=0.78,
158÷200=0.79,
321÷400=0.8025,
801÷1000=0.801,
∴ 估计这名运动员射击一次“射中 9 环以上”的概率是 0.80.
第三部分
17.
∵x2+x3x−4=0,∴x2+3x2−4x=0.4x2−4x=0.∴4xx−1=0.
则
4x=0 或 x−1=0.
解得
x1=0,x2=1.
18. 如图所示:△A′B′O 即为所求.
19. 记小美、爸爸和妈妈分别为 A,B,C,
则三人排成一排有如下 6 种等可能结果:
ABC,ACB,BAC,BCA,CAB,CBA,
其中小美排在妈妈右侧身旁的有 ACB 和 BAC 两种情况,
所以小美排在妈妈右侧身旁的概率为 26=13.
20. (1) ∵ 函数 y=kx 的图象过点 A3,1,
∴k=xy=3×1=3.
(2) ∵B2,0,
∴OB=2,
∵△AOB 绕点 O 逆时针旋转 60∘ 得到 △COD,
∴OD=OB=2,∠BOD=60∘,
如图,过点 D 作 DE⊥x 轴于点 E,
DE=OD⋅sin60∘=2×32=3,
OE=OD⋅cs60∘=2×12=1,
∴D1,3,
由(1)可知 y=3x,
∴ 当 x=1 时,y=31=3,
∴D1,3 在反比例函数 y=3x 的图象上.
21. 分两种情况考虑:
当两条弦位于圆心 O 一侧时,如图 1 所示,
过 O 作 OE⊥CD,交 CD 于点 E,交 AB 于点 F,连接 OC,OA,
∵AB∥CD,
∴ OE⊥AB,
∴ E,F 分别为 CD,AB 的中点,
∴ CE=DE=12CD=3 cm,AF=BF=12AB=4 cm,
在 Rt△AOF 中,OA=5 cm,AF=4 cm,
根据勾股定理得:OF=3 cm,
在 Rt△COE 中,OC=5 cm,CE=3 cm,
根据勾股定理得:OE=4 cm,
则 EF=OE−OF=4 cm−3 cm=1 cm;
当两条弦位于圆心 O 两侧时,如图 2 所示,
同理可得 EF=4 cm+3 cm=7 cm,
综上,弦 AB 与 CD 的距离为 7 cm 或 1 cm.
22. (1) ∵ 在方程 x2−k+3x+2k+2=0 中,Δ=−k+32−4×1×2k+2=k2−2k+1=k−12≥0,
∴ 方程总有两个实数根.
(2) ∵x2−k+3x+2k+2=x−2x−k−1=0,
∴x1=2,x2=k+1.
∵ 方程有一根小于 1,
∴k+1<1,解得 k<0,
∴k 的取值范围为 k<0.
23. (1) 设铁皮各角应切去边长是 x 分米的正方形,
则无盖方盒的底面是长为 10−2x 分米、宽为 8−2x 分米的矩形,
由题意得:
10−2x8−2x=48.
整理得:
x2−9x+8=0.
解得:
x1=1,x2=8.∵8−2x>0
,
∴x<4,
∴x=1.
答:铁皮各角应切去边长是 1 分米的正方形.
(2) 设铁皮各角切去边长是 m 分米的正方形,防锈处理所需总费用为 w 元,
∵ 制作的无盖方盒的底面长不大于底面宽的 3 倍,
∴10−2m≤38−2m,解得:m≤72.
根据题意得:
w=0.5×2×m10−2m+m8−2m+210−2m8−2m=4m2−54m+160,
∴a=4,b=−54,
∴ 当 0
答:当铁皮各角切去边长是 72 分米的正方形时,总费用最低,最低费用为 20 元.
24. (1) ∵∠ACB=90,
∴∠ACD+∠BCD=90∘,
∵AC 为 ⊙O 的直径,
∴∠ADC=∠BDC=90∘,
∴∠B+∠BDC=90∘,
∴∠B=∠ACD,
连接 OD,如图 1,
∵DE 为 ⊙O 的切线,
∴∠ODE=∠ODC+∠CDE=90∘,
∵∠CDE+∠BDE=90∘,
∵OC=OD,
∴∠ACD=∠ODC,
∴∠ODC=∠BDE=∠B,
∴DE=BE,同理可得 DE=CE,
∴CE=BE,Rt△CDB 中,DE=12BC.
(2) 如图 2,由(1)知:BE=DE,
∵ED=FD,
∴BE=12EF,
∵BG 是 △BDE 的中线,
∴EG=DG=12DE,
∴EGBE=BEEF=12,
∵∠BEG=∠BEF,
∴△BEG∽△FEB,
∴BGBF=EGBE=12,
∴BF=2BG.
25. (1) 过点 C 作 KC⊥x 轴交于点 K,
∵∠BAO+∠CAK=90∘,∠BAO+∠CAK=90∘,
∴∠CAK=∠OBA,
又 ∠AOB=∠AKC=90∘,AB=AC,
∴△ABO≌△CAKAAS,
∴OB=AK=2,AO=CK=1,故点 C 的坐标为 3,1,
将点 C 的坐标代入二次函数表达式得 1=12×9+3b−2,解得 b=−12,
故二次函数表达式为:y=12x2−12x−2. ⋯⋯①
(2) 设若直线 l 与直线 BC,AC 分别交于点 M,N,
把点 B,C 的坐标代入一次函数表达式 y=kx+2,得 1=3k+2,
解得 k=−13,即直线 BC 的表达式为 y=−13x+2,
同理可得直线 AC 的表达式为 y=12x−12,
直线 AB 的表达式为 y=−2x+2,
设点 M 的坐标为 x,−13x+2 、点 N 坐标为 x,12x−12,
直线 l 恰好将 △ABC 的面积分为 1:2 两部分,
设 S△CMN=13S△ACB 或 S△CMN=23S△ACB,
即 12×3−x−13x+2−12x+12=12×5×5×13 或 12×3−x−13x+2−12x+12=12×5×5×23,
解得 x=3−2 或 1(不合题意的值已舍去),
即直线 l 与 x 轴的交点坐标为 1,0 或 3−2,0.
(3) 将 △ABC 以 AC 所在直线为对称轴翻折 180∘,点 Bʹ 的坐标为 2,−2,
①当 ∠PCBʹ=90∘ 时,
∵∠BCBʹ=90∘,故点 P 为直线 BC 与抛物线的另外一个交点,
直线 BC 的方程为 y=−13x+2, ⋯⋯②
联立 ①② 解得 x=3 或 −83,故点 P 的坐标为 −83,269;
②当 ∠CPBʹ=90∘ 时,同理可得点 P 的坐标为 −1,−1 或 43,−169.
故点 P 的坐标为 −83,269 或 −1,−1 或 43,−169.
2018_2019学年广州市白云区九上期末数学试卷: 这是一份2018_2019学年广州市白云区九上期末数学试卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2018-2019学年广东省广州市白云区九上期末数学试卷: 这是一份2018-2019学年广东省广州市白云区九上期末数学试卷,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2018-2019学年广东省广州市白云区八下期末数学试卷: 这是一份2018-2019学年广东省广州市白云区八下期末数学试卷,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












